基于先验信息的改进随机约束两参数估计 Improved Stochastic Restricted Two-Parameter Estimation Based on Prior Information

doi:10.12677/AAM.2020.911216

Advances in Applied Mathematics
Vol. 09 No. 11 ( 2020 ), Article ID: 38548 , 8 pages
10.12677/AAM.2020.911216

基于先验信息的改进随机约束两参数估计

陈景，陈菊，李荣

●How to Cite this Article

贵州民族大学，贵州贵阳

收稿日期：2020年10月16日；录用日期：2020年11月3日；发布日期：2020年11月10日

摘要

本文主要针对一般线性模型中存在复共线性的情况，结合随机约束条件下的混合估计和基于先验信息的两参数估计提出了一种新的有偏估计，即随机约束改进两参数估计。并在均方误差矩阵准则的意义下研究了随机约束改进两参数估计相对于两参数估计、改进两参数估计混合估计、随机约束岭估计和随机约束两参数估计的优良性。进一步，讨论了偏置参数的选择。同时，通过一个数值算例对所提出的估计的性能进行了说明。

关键词

均方误差矩阵，混合估计，随机线性约束，改进两参数估计

Improved Stochastic Restricted Two-Parameter Estimation Based on Prior Information

Jing Chen, Ju Chen, Rong Li

Guizhou Minzu University, Guiyang Guizhou

Received: Oct. 16^th, 2020; accepted: Nov. 3^rd, 2020; published: Nov. 10^th, 2020

ABSTRACT

This paper mainly aims at the situation where there is complex collinearity in the general linear model. Combining the mixed estimator under the condition of stochastic restricted and the two-parameter estimator of parameter vectors based on prior information, a new biased estimator is proposed, that is, the stochastic constrained modified two-parameter estimator. In the sense of mean square error matrix criterion, the superiority of stochastic constrained modified two-parameter estimator relative to two-parameter estimator, modified two-parameter estimator, mixed estimator, stochastic restricted ridge estimator and stochastic restricted two-parameter estimator are studied. Further, the selection of bias parameters is discussed. At the same time, the performance of the proposed estimator is explained through a numerical example.

Keywords:Mean Squared Error Matrix, Mixed Estimator, Stochastic Linear Restrictions, Modified Two-Parameter Estimator

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 介绍

考虑线性回归模型的一般形式为：

$y = X β + ε$ (1)

其中y为 $n \times 1$ 的观测向量；X为 $n \times p$ 的设计矩阵； $β$ 为 $p \times 1$ 的未知参数向量； $ε$ 为 $n \times 1$ 的随机误差向量。在这里，我们假定 $ε$ 的均值向量和协方差矩阵分别为 $E (ε) = 0$ 和 $C o v (ε) = σ^{2} I_{n}$ ，其中 $I_{n}$ 是n阶单位矩阵。

在模型(1)中参数向量 $β$ 的最小二乘估计(OLSE)定义为：

${\hat{β}}_{L} = {(X^{'} X)}^{- 1} X^{'} y$ (2)

当自变量之间出现复共线性时，最小二乘估计不再是良好的估计。为此，相关学者提出了有偏估计作为OLSE的替代估计，以克服复共线性问题。如：岭估计，Liu估计以及两参数估计(TPE)。分别表示如下：

$\hat{β} (k) = {(X^{'} X + k I)}^{- 1} X^{'} X {\hat{β}}_{L}$ (3)

$\hat{β} (d) = {(X^{'} X + I)}^{- 1} (X^{'} X + d I) {\hat{β}}_{L}$ (4)

$\hat{β} (k, d) = {(X^{'} X + k I)}^{- 1} (X^{'} X + k d) {\hat{β}}_{L}$ (5)

其中 $k > 0$ ， $0 < d < 1$ 。

关于参数向量 $β$ 的估计，相关学者考虑存在一个关于 $β$ 的先验信息b，结合其他有偏估计提出了一系列的改进估计。如Swindel [1] 提出了改进岭估计(MRRE)，Li和Yang [2] 提出了改进Liu估计(MLE)等。运用类似的方法，Adewale [3] 结合先验信息和两参数估计(Özkale和Kaciranlar [4] )提出了改进两参数估计(MTPE)。分别表示如下：

$\hat{β} (k, b) = {(X^{'} X + k I)}^{- 1} (X^{'} X {\hat{β}}_{L} + k b)$ (6)

$\hat{β} (d, b) = {(X^{'} X + I)}^{- 1} ((X^{'} X + d I) {\hat{β}}_{L} + (1 - d) b)$ (7)

$\hat{β} (k, d, b) = {(X^{'} X + k I)}^{- 1} ((X^{'} X + k d) {\hat{β}}_{L} + k (1 - d) b)$ (8)

其中 $k > 0$ ， $0 < d < 1$ ，b是 $β$ 的先验信息。

另一方面，可以通过对模型(1)添加等式或随机约束的方式来克服多重共线性对参数估计的影响。本文我们假设参数向量受如下随机线性约束：

$r = R β + e$ (9)

其中r为 $m \times 1$ 的已知随机向量；R为 $m \times p$ 的已知元素矩阵；e为 $m \times 1$ 的随机误差向量。在这里，我们假定e的均值向量和协方差矩阵分别为 $E (e) = 0$ 和 $C o v (e) = σ^{2} V$ ，并假定V是已知的正定矩阵。进一步，我们还假设随机向量 $ε$ 随机独立于e。

Theil和Goldberger [5] 通过构建下面的增广矩阵模型：

$(\begin{matrix} y \\ r \end{matrix}) = (\begin{matrix} X \\ R \end{matrix}) β + (\begin{matrix} ε \\ e \end{matrix})$ (10)

或表示如下：

$y_{m} = X_{m} β + u_{m}$ (11)

其中 $y_{m} = (\begin{matrix} y \\ r \end{matrix})$ ， $X_{m} = (\begin{matrix} X \\ R \end{matrix})$ ， $u_{m} = (\begin{matrix} ε \\ e \end{matrix})$ ， $E (u_{m}) = 0$ ， $C o v (u_{m}) = σ^{2} N = σ^{2} (\begin{matrix} I & 0 \\ 0 & V \end{matrix})$ 。

并运用最小二乘法得到了 $β$ 的混合估计(OME)：

${\hat{β}}_{m} = {(S + R^{'} V^{- 1} R)}^{- 1} (X^{'} y + R^{'} V^{- 1} r)$ (12)

其中 $S = X^{'} X$ 。混合估计 ${\hat{β}}_{m}$ 也可以通过求解以下极值问题而得到：

$Ψ_{1} = {(y_{m} - X_{m} β)}^{'} (y_{m} - X_{m} β) + {(r - R β)}^{'} V^{- 1} (r - R β)$

运用类似的方法Özkale等人 [6] 得到模型(11)中 $β$ 的随机约束岭估计(SRRE)。Hu Yang等人 [7] 提出了一种新的估计方法，称为随机约束两参数估计(SRTPE)。分别表示如下：

${\hat{β}}_{S S R E} = {(S + R^{'} V^{- 1} R + k I)}^{- 1} (X^{'} y + R^{'} V^{- 1} r)$ (13)

${\hat{β}}_{y - m} (k, d) = {(S + R^{'} V^{- 1} R + k I)}^{- 1} (X^{'} y + R^{'} V^{- 1} r + k d {\hat{β}}_{L})$ (14)

结合带随机约束的线性模型和基于先验信息的改进两参数估计，我们提出了新估计，即基于先验信息的改进随机约束两参数估计(SRMTPE)，如下：

$\begin{matrix} {\hat{β}}_{y - m} (k, d, b) = {(S + R^{'} V^{- 1} R + k I)}^{- 1} (X^{'} y + R^{'} V^{- 1} r + k d {\hat{β}}_{L} + k (1 - d) b) \\ = {(S + R^{'} V^{- 1} R + k I)}^{- 1} ((S + k d I) {\hat{β}}_{L} + R^{'} V^{- 1} r + k (1 - d) b) \end{matrix}$ (15)

已知：

${\hat{β}}_{y - m} (0, 0, b) = {\hat{β}}_{m}$ ； ${\hat{β}}_{y - m} (k, 1, 0) = {\hat{β}}_{y - m} (k, d)$ ； ${\hat{β}}_{y - m} (k, d, 0) = {\hat{β}}_{y - m} (k, d)$

${\hat{β}}_{y - m} (k, 1, b) = {\hat{β}}_{m}$ ， $k \in R, k \neq 0$ ； ${\hat{β}}_{y - m} (k, 0, 0) = {\hat{β}}_{S S R E}$ ； ${\hat{β}}_{y - m} (0, 0, b) = {\hat{β}}_{y - m} (0, 1, b) = {\hat{β}}_{L}$ ；

$R = 0$ ， ${\hat{β}}_{y - m} (k, d, b) = \hat{β} (k, d, b)$ 。

因此，可以认为随机约束改进两参数估计 ${\hat{β}}_{y - m} (k, d, b)$ 是OLSE、ME、SRRE、SRTPE、MTPE估计的推广。

我们可以得到的新估计 ${\hat{β}}_{y - m} (k, d, b)$ 的均值向量和协方差矩阵分别为：

$\begin{array}{l} E ({\hat{β}}_{y - m} (k, d, b)) \\ = {(X^{'} X + R^{'} V^{- 1} R + k I)}^{- 1} β (X^{'} X + R^{'} V^{- 1} R + k d I) + k (1 - d) b {(X^{'} X + R^{'} V^{- 1} R + k I)}^{- 1} \\ = M (k) ((S (k d) + R^{'} V^{- 1} R) β + k (1 - d) b) \end{array}$ (16)

$C o v ({\hat{β}}_{y - m} (k, d, b)) = σ^{2} M (k) (S + k^{2} d^{2} S^{- 1} + R^{'} V^{- 1} R) M (k)$ (17)

其中 $M (k) = {(X^{'} X + R^{'} V^{- 1} R + k I)}^{- 1}$ 。

从式(16)可知 ${\hat{β}}_{y - m} (k, d, b)$ 是有偏估计。

2. 均方误差矩阵意义下新估计的优良性

在本节中，我们使用均方误差矩阵(MSEM)准则来研究随机约束改进两参数估计(SRMPTE)估计的性能。

首先，我们给出 $β$ 的任一个估计 ${\hat{β}}^{*}$ 的均方误差矩阵(MSEM)的定义如下：

$M S E M ({\hat{β}}^{*}) = E ({\hat{β}}^{*} - β) {({\hat{β}}^{*} - β)}^{'} = C o v ({\hat{β}}^{*}) + B i a s ({\hat{β}}^{*}) B i a s {({\hat{β}}^{*})}^{'}$

其中 $C o v ({\hat{β}}^{*})$ 是方差矩阵， $B i a s ({\hat{β}}^{*})$ 是偏差向量，且 $B i a s ({\hat{β}}^{*}) = E ({\hat{β}}^{*}) - β$ 。

假设 ${\hat{β}}_{1}$ ， ${\hat{β}}_{2}$ 为参数向量 $β$ 的两个估计，则 ${\hat{β}}_{1}$ 在均方误差矩阵意义下优于 ${\hat{β}}_{2}$ 当且仅当 $M S E M ({\hat{β}}_{2}) - M S E M ({\hat{β}}_{1}) \geq 0$ ，即差值为正定或半正定矩阵。

引理1. 假设M是一个正定矩阵，即 $M > 0$ ， $α$ 是一个向量，当且仅当 $α^{'} M^{- 1} α \leq 1$ 时 $M - α^{'} α \geq 0$ 。

引理2. 假设M是一个正定矩阵，N是非负定矩阵。然后有 $M - N \geq 0 \Leftrightarrow λ_{\max} (N M^{- 1}) \leq 1$ 。

2.1. ME和SRMTPE的MSEM性能比较

ME估计的偏差向量和和协方差矩阵如下：

$B i a s ({\hat{β}}_{m}) = E ({\hat{β}}_{m}) - β = 0$ ， $C o v ({\hat{β}}_{m}) = σ^{2} {(S + R^{'} V^{- 1} R)}^{- 1}$ ，

因此，其均方误差矩阵为：

$M S E M ({\hat{β}}_{m}) = σ^{2} {(S + R^{'} V^{- 1} R)}^{- 1}$ 。

对于SRMTPE估计，我们进一步有估计 ${\hat{β}}_{y - m} (k, d, b)$ 的偏差向量和均方误差矩阵为：

$B i a s ({\hat{β}}_{y - m} (k, d, b)) = k (d - 1) M (k) (β - b)$ ，

$M S E M ({\hat{β}}_{y - m} (k, d, b)) = σ^{2} M (k) (S + k^{2} d^{2} S^{- 1} + R^{'} V^{- 1} R) + k^{2} {(d - 1)}^{2} M (k) (β - b) {(β - b)}^{'} M (k)$ 。

其中 $S (k) = X^{'} X + k I$ ， $S (k d) = X^{'} X + k d I$ ， $M (k) = {(X^{'} X + R^{'} V^{- 1} R + k I)}^{- 1}$ 。

所以，ME估计与SRMTPE估计之间的MSEM差值如下所示：

$\begin{matrix} Δ_{1} = M S E M ({\hat{β}}_{m}) - M S E M ({\hat{β}}_{y - m} (k, d, b)) \\ = M (k) (σ^{2} M_{1} - k^{2} {(d - 1)}^{2} (β - b) {(β - b)}^{'}) M ( k ) \end{matrix}$

其中 $M_{1} = 2 k I + k^{2} ({(X^{'} X + R^{'} V^{- 1} R)}^{- 1} - d^{2} {(X^{'} X)}^{- 1})$ 。

进一步，我们可以得到以下定理。

定理1. 如果 $d^{2} \leq λ_{\min} {(S + R^{'} V^{- 1} R)}^{- 1} S$ ，那么 $Δ_{1} \geq 0$ ，则称在均方误差矩阵准则下 ${\hat{β}}_{y - m} (k, d, b)$ 优于 ${\hat{β}}_{m}$ ，当且仅当 $k^{2} {(d - 1)}^{2} {(β - b)}^{'} M_{1}^{- 1} (β - b) \leq σ^{2}$ 。

2.2. MTPE与SRMTPE的MSEM性能比较

MTPE估计的偏差向量和协方差矩阵如下：

$B i a s (\hat{β} (k, d, b)) = k (d - 1) M (k) (β - b)$ ， $C o v (\hat{β} (k, d, b)) = σ^{2} S {(k)}^{- 1} S (k d) S^{- 1}$ ，

因此，其均方误差矩阵为：

$M S E M (\hat{β} (k, d, b)) = σ^{2} S {(k)}^{- 1} S (k d) S^{- 1}$ 。

MTPE估计与SRMTPE估计之间的MSEM差值如下所示：

$\begin{matrix} Δ_{2} = M S E M (\hat{β} (k, d, b)) - M S E M ({\hat{β}}_{y - m} (k, d, b)) \\ = M (k) (σ^{2} M_{2} - k^{2} {(d - 1)}^{2} (β - b) {(β - b)}^{'}) M ( k ) \end{matrix}$

其中 $M_{2} = 2 k I + k^{2} ({(X^{'} X + k I)}^{- 1} (X^{'} X + k d I) {(X^{'} X)}^{- 1} - d^{2} {(X^{'} X)}^{- 1})$ 。

类似的，我们可以得到以下定理。

定理2. 如果 $d^{2} \leq λ_{\min} S {(k)}^{- 1} S (k d)$ ，那么 $Δ_{2} \geq 0$ ，则称在均方误差矩阵准则下 ${\hat{β}}_{y - m} (k, d, b)$ 优于 $\hat{β} (k, d, b)$ ，当且仅当 $k^{2} {(d - 1)}^{2} {(β - b)}^{'} M_{2}^{- 1} (β - b) \leq σ^{2}$ 。

2.3. SRTPE与SRMTPE的MSEM性能比较

SRTPE估计的偏差向量和协方差矩阵如下：

$B i a s ({\hat{β}}_{y - m} (k, d)) = k (d - 1) M (k) β$ ， $C o v ({\hat{β}}_{y - m} (k, d)) = σ^{2} M (k) (S + k^{2} d^{2} S^{- 1} + R^{'} V^{- 1} R) M (k)$ 。

因此，其均方误差矩阵为：

$M S E M ({\hat{β}}_{y - m} (k, d)) = σ^{2} M (k) (S + k^{2} d^{2} S^{- 1} + R^{'} V^{- 1} R) + k^{2} {(d - 1)}^{2} M (k) β β^{'} M (k)$ ，

SRTPE估计与SRMTPE估计之间的MSEM差值如下所示：

$\begin{matrix} Δ_{3} = M S E M ({\hat{β}}_{y - m} (k, d)) - M S E M ({\hat{β}}_{y - m} (k, d, b)) \\ = k^{2} {(d - 1)}^{2} M (k) (β β^{'} - (β - b) {(β - b)}^{'}) M ( k ) \end{matrix}$

在Li和Yang [8] 采用先验信息 $b = 0.95 {\hat{β}}_{L}$ ，所以当 $(β β^{'} - (β - b) {(β - b)}^{'}) \geq 0$ 时， $Δ_{3} \geq 0$ 。所以，

我们有以下定理：

定理3. 对于 $0 < d < 1, k > 0$ ，在均方误差矩阵准则下 ${\hat{β}}_{y - m} (k, d, b)$ 优于 ${\hat{β}}_{y - m} (k, d)$ 。

2.4. SSRE与SRMTPE的MSEM性能比较

SSRE估计的偏差向量和协方差矩阵如下：

$B i a s ({\hat{β}}_{S S R E}) = - k {(X^{'} X + R^{'} V^{- 1} R + k I)}^{- 1} β$ ， $C o v ({\hat{β}}_{S S R E}) = σ^{2} M (k) (S + R^{'} V^{- 1} R) M (k)$ ，因此，其均方误差矩阵为：

$M S E M ({\hat{β}}_{S S R E}) = σ^{2} M (k) (S + R^{'} V^{- 1} R + k^{2} β β^{'}) M ( k )$

SSRE估计与SRMTPE估计之间的MSEM差值如下所示：

$\begin{matrix} Δ_{4} = M S E M ({\hat{β}}_{S S R E}) - M S E M ({\hat{β}}_{y - m} (k, d, b)) \\ = M (k) (σ^{2} M_{3} + k^{2} (β β^{'} - {(d - 1)}^{2} (β - b) {(β - b)}^{'})) M ( k ) \end{matrix}$

其中

$M_{3} = X^{'} X - (X^{'} X + k d I) {(X^{'} X)}^{- 1} (X^{'} X + k d I) = X^{'} X (I - {(X^{'} X)}^{- 1} (X^{'} X + k d I) {(X^{'} X)}^{- 1} (X^{'} X + k d I))$

进一步，如果 $I - {(X^{'} X)}^{- 1} (X^{'} X + k d I) {(X^{'} X)}^{- 1} (X^{'} X + k d I) > 0$ ，那么 $Δ_{4}$ 是正定的。既有 $γ_{i} = 1 - \frac{{(λ_{i} + k d)}^{2}}{λ_{i}^{2}}$ ， $γ_{i}$ 为其特征值。由于 $0 < d < 1, k > 0$ ，所以当 $λ_{i} < \frac{k d}{2}$ 时， $1 - \frac{{(λ_{i} + k d)}^{2}}{λ_{i}^{2}} > 0$ 。因此，我们可以表述如下定

理：

定理4. 对于 $0 < d < 1, k > 0$ ，当 $λ_{i} < \frac{k d}{2}$ 时，在均方误差矩阵准则下 ${\hat{β}}_{y - m} (k, d, b)$ 优于 ${\hat{β}}_{y - m} (k, d)$ 。

2.5. TPE与SRMTPE的MSEM性能比较

TPE估计的偏差向量和协方差矩阵如下：

$B i a s (\hat{β} (k, d)) = k (d - 1) S {(k)}^{- 1} β$ ， $C o v (\hat{β} (k, d)) = σ^{2} S {(k)}^{- 1} S (k d) S^{- 1} S (k d) S {(k)}^{- 1}$ ；

因此，其均方误差矩阵为：

$M S E M (\hat{β} (k, d)) = σ^{2} M (k) (S + R^{'} V^{- 1} R + k^{2} β β^{'}) M (k) + k^{2} {(d - 1)}^{2} S {(k)}^{- 1} β β^{'} S {(k)}^{- 1}$

TPE估计与SRMTPE估计之间的MSEM差值如下所示：

$\begin{matrix} Δ_{5} = M S E M (\hat{β} (k, d)) - M S E M ({\hat{β}}_{y - m} (k, d, b)) \\ = σ^{2} M (k) (S + R^{'} V^{- 1} R + k^{2} β β^{'}) M (k) + k^{2} {(d - 1)}^{2} S {(k)}^{- 1} β β^{'} S {(k)}^{- 1} \\ - σ^{2} M (k) (S + k^{2} d^{2} S^{- 1} + R^{'} V^{- 1} R) - k^{2} {(d - 1)}^{2} M (k) (β - b) {(β - b)}^{'} M (k) \\ = A - B \end{matrix}$

其中 $A = M S E M (\hat{β} (k, d))$ ， $B = σ^{2} M (k) (S + k^{2} d^{2} S^{- 1} + R^{'} V^{- 1} R) + k^{2} {(d - 1)}^{2} M (k) (β - b) {(β - b)}^{'} M ( k )$

由于A是正定的，如果 $A - B \geq 0$ ，即 $A \geq B$ ，那么 $I \geq A^{- 1 / 2} B A^{- 1 / 2}$ 。所以， $Δ_{5} \geq 0$ 的充分必要条件是 $λ_{\max} (A^{- 1} B) \leq 1$ ，其中 $λ_{\max} (A^{- 1} B) \leq 1$ 为 $A^{- 1} B$ 的最大特征值。现在我们给出下面的定理。

定理5. 当且仅当 $λ_{\max} (A^{- 1} B) \leq 1$ ，在均方误差矩阵准则下 ${\hat{β}}_{y - m} (k, d, b)$ 优于 $\hat{β} (k, d)$ 。

3. 参数k和d的选择

在本节中，我们将讨论用均方误差(MSE)准则选择参数k和d。我们可以首先计算SRMPTE的MSE：

$\begin{matrix} f (k, d, b) = M S E ({\hat{β}}_{y - m} (k, d, b)) = t r [M S E M ({\hat{β}}_{y - m} (k, d, b))] \\ = σ^{2} t r [M (k) (S + k^{2} d^{2} S^{- 1} + R^{'} V^{- 1} R) M (k)] + k^{2} {(d - 1)}^{2} {(β - b)}^{'} M (k) M (k) (β - b) \end{matrix}$

通过使函数 $f (k, d, b)$ 最小化，可以得到d和k的最优值。对于固定的k，函数 $f (k, d, b)$ 关于d求偏导有：

$\frac{\partial f (k, d, b)}{\partial d} = 2 σ^{2} k^{2} d [t r (M (k) S^{- 1} M (k))] + 2 k^{2} (d - 1) [t r (M (k) (β - b) {(β - b)}^{'} M (k))]$

因此，我们可以通过 $\frac{\partial f (k, d, b)}{\partial d} = 0$ 得到d的最优值，这是由：

${\hat{d}}_{o p t} = \frac{t r (M (k) (\hat{β} - b) {(\hat{β} - b)}^{'} M (k))}{t r [M (k) ({\hat{σ}}^{2} S^{- 1} + (\hat{β} - b) {(\hat{β} - b)}^{'}) M (k)]}$

其中 $\hat{β}, {\hat{σ}}^{2}$ 是 $β, σ^{2}$ 相应的估计。对于固定的d值，关于参数k的最优选择同样通过对函数 $f (k, d, b)$ 求偏导得到。接下来我们考虑通过一个实证进一步探讨随机约束改进两参数估计的优良性。

4. 数值例子

我们考虑Gruber (1998)中讨论的数据资料，即1972~1986年法国、德国、日本、前苏联与美国国家研究与开发支出占国民生产总值的百分比，分别记为 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ 与y，以用来分析随机约束改进两参数估计的优良性。数据资料矩阵如下：

$X = (x_{1}, x_{2}, x_{3}, x_{4}) = (\begin{matrix} 1.9 & 2.2 & 1.9 & 3.7 \\ 1.8 & 2.2 & 2.0 & 3.8 \\ 1.8 & 2.4 & 2.1 & 3.6 \\ 1.8 & 2.4 & 2.2 & 3.8 \\ 2.0 & 2.5 & 2.3 & 3.8 \\ 2.1 & 2.6 & 2.4 & 3.7 \\ 2.1 & 2.6 & 2.6 & 3.8 \\ 2.2 & 2.6 & 2.6 & 4.0 \\ 2.3 & 2.8 & 2.8 & 3.7 \\ 2.3 & 2.7 & 2.8 & 3.8 \end{matrix})$ ， $y = (\begin{matrix} 2.3 \\ 2.2 \\ 2.2 \\ 2.3 \\ 2.4 \\ 2.5 \\ 2.6 \\ 2.6 \\ 2.7 \\ 2.7 \end{matrix})$

我们可以计算出如下 $β, σ^{2}$ 的最小二乘估计(OLSE)：

，

在这里考虑如下随机线性约束：

，，

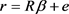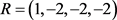在几组不同的参数k，d值下，通过计算相应的均方误差表达式，容易得到与之相应的两参数估计、改进两参数估计、混合估计、随机约束岭估计和随机约束两参数估计的均方误差值，见表1。

从表1可以看出，当参数(k, d)取以上几组参数值时，随机约束改进两参数估计的均方误差值均小于两参数估计、改进两参数估计、混合估计、随机约束岭估计和随机约束两参数估计的均方误差值。即随机约束改进两参数估计在均方误差意义下优于两参数估计、改进两参数估计、混合估计、随机约束岭估计和随机约束两参数估计。这表明我们提出的随机约束改进两参数估计在实际中是有意义的。

Table 1. Estimated MSE values of the TPE, MTPE, ME, SRRE, SRTPE and SRMTPE

表1. TPE、MTPE、ME、SRRE、SRTPE和SRMTPE估计的MSE值

5. 结论

本文在带随机约束的线性模型中结合了考虑先验信息的参数向量的两参数估计，以克服线性回归模型中存在复共线性的问题。并分别通过理论和实证分析，在均方误差矩阵和均方误差意义下探讨了随机约束改进两参数估计的优良性。在理论分析中，得到了随机约束改进两参数估计在均方误差矩阵优于两参数估计、改进两参数估计、混合估计、随机约束岭估计和随机约束两参数估计的充要条件。实证结果表明，在均方误差意义下，随机约束改进两参数估计相对于两参数估计、改进两参数估计、混合估计、随机约束岭估计和随机约束两参数估计具有一定的优越性。

基金项目

贵州民族大学自然科学基金项目(黔科合平台人才[2018]5773-YB04)。

文章引用

陈景,陈菊,李荣. 基于先验信息的改进随机约束两参数估计
Improved Stochastic Restricted Two-Parameter Estimation Based on Prior Information[J]. 应用数学进展, 2020, 09(11): 1879-1886. https://doi.org/10.12677/AAM.2020.911216

参考文献

1. Swindel, B.F. (1976) Good Ridge Estimators Based on Prior Information. Communications in Statistics Theory and Methods, 5, 1065-1075. https://doi.org/10.1080/03610927608827423

2. Li, Y.L. and Yang, H. (2012) A New Liu-Type Estimator in Linear Regression Model. Statistical Papers, 53, 427-437. https://doi.org/10.1007/s00362-010-0349-y

3. Lukman, A.F., Ayinde, K., Kun, S.S. and Adewuyi, E.T. (2019) A Modified New Two-Parameter Estimator in a Linear Regression Model. Modelling and Simulation in Engineering, 2019, Article ID: 6342702. https://doi.org/10.1155/2019/6342702

4. Özkale, M.R. and Kaciranlar, S. (2007) The Restricted and Unrestricted Two-Parameter Estimators. Communications in Statistics Theory and Methods, 36, 2707-2725. https://doi.org/10.1080/03610920701386877

5. Theil, H. (1963) On the Use of Incomplete Prior Information in Regression Analysis. Journal of the American Statistical Association, 58, 401-414. https://doi.org/10.1080/01621459.1963.10500854

6. ÖZkale, M.R. (2009) A Stochastic Restricted Ridge Regression Estimator. Journal of Multivariate Analysis, 100, 1706-1716. https://doi.org/10.1016/j.jmva.2009.02.005

7. Yang, H. and Cui, J. (2011) A Stochastic Restricted Two-Parameter Estimator in Linear Regression Model. Communications in Statistics Theory and Methods, 40, 2318-2325. https://doi.org/10.1080/03610921003778217

8. Li, Y.L. and Yang, H. (2011) A New Ridge-Type Estimator in Stochastic Restricted Linear Regression. Statistics, 45, 123-130. https://doi.org/10.1080/02331880903573153

期刊菜单