Advances in Applied Mathematics
Vol.
10
No.
08
(
2021
), Article ID:
44302
,
6
pages
10.12677/AAM.2021.108273
Stern偏序集的flag f和flag h向量的性质研究
林佳倩
辽宁师范大学数学学院,辽宁 大连

收稿日期:2021年7月2日;录用日期:2021年7月21日;发布日期:2021年8月3日

摘要
Stern偏序集是组合数学中一类非常重要且有趣的偏序集,在组合计数中起到重要的统一作用。本篇论文从计数序理想角度出发,研究了Stern偏序集的flag f和flag h向量,并给出了具体表达公式。
关键词
Stern偏序集,flag f向量,flag h向量

The flag f and flag h Vectors of the Stern’s Poset
Jiaqian Lin
School of Mathematics, Liaoning Normal University, Dalian Liaoning

Received: Jul. 2nd, 2021; accepted: Jul. 21st, 2021; published: Aug. 3rd, 2021

ABSTRACT
The Stern’s poset is one kind of partially ordered set with great importance and interest in Combinatorics, which plays a unifying role in combinatorial counting. In this paper, we study the flag f and flag h vectors of the Stern’s poset from the viewpoint of counting order ideal, and then give the specific expression formulas.
Keywords:Stern’s Poset, flag f Vector, flag h Vector

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设P是一个非空集合,如果在P的元素中定义一个二元关系
,满足:
1) 自反性:对所有P中元素x都有
;
2) 反对称性:如果
且
则有
;
3) 传递性:如果
且
则有
。
那么
称为P上的一个偏序,P连同此偏序
称为一个偏序集,记为
,简记为P。若偏序集P中存在元素x满足对所有的
都有
(
),则称x是P的极小元(极大元),记为
(
)。若
且没有P中元素z满足
成立,则称y覆盖x并记为
。每个偏序集都唯一的由它上面的覆盖关系决定。将偏序集中的每个元素画成一个点,任意两点间有边相连当且仅当这两点间有覆盖关系,这样得到的图称为偏序集的Hasse图,下面是一些常见的偏序集及其对应的Hasse图。
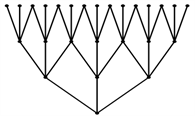
例1.1偏序集
:集合P是[n]的所有子集合
,二元关系
定义为子集的包含关系。如图1所示,
图1.
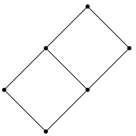
例1.2偏序集
:集合P是正整数n的所有因子,二元关系
定义为整除关系。如图2所示,
图2.
偏序集是现代数学的重要研究对象,是组合数学与其他数学分支之间联系的桥梁与纽带,在组合数学的研究中起着重要的统一作用 [1] [2]。本文我们研究了Stern偏序集。
Pascal三角是数学中非常著名的三角,它的前几项如图3所示。
类似于Pascal三角,我们也从一行中“向下”复制每个数字得到下一行,从而得到Stern三角。如图4所示。
图3. Pascal三角
图4. Stern 三角
将Stern三角上下翻转,Stern三角中的每一个元素用
表示,对Stern三角中的元素定义序关系,满足:
当且仅当
且
。最小元素
,我们得到Stern偏序集如图5所示。
图5. Stern偏序集
R. Stanley定义了Stern偏序集并证明了对一个固定整数
,第n行元素的第n次幂和
满足常系数线性递归 [3]。通过对Stern偏序集主理想的计数可以得到许多组合序列。
下面介绍组合学中的一些基本概念(详见 [4],Ch3)。设P是秩为n的有限偏序集,其秩函数
。如果
,定义子偏序集
,称为P的S级子偏序集。定义
(或简记为
)为
的最大链数。例如,
(
的简称)是P中秩为i的元素个数。定义函数
为P的flag f向量。通过公式
定义
,函数
称为P的flag h向量。
和
这两个函数自然地出现在数学的不同领域,并得到广泛的研究 [5] [6]。2020年,牟丽丽通过建立Hexagonal格路的n阶理想与Schröder路的阶理想的双射关系给出了Hexagonal偏序集的一些组合性质,并给出了Hexagonal偏序集的flag f和flag h向量的递归公式 [7]。同年,牟丽丽与我研究了J. Propp通过对Ferrers图进行变换得到的Hexagonal偏序集、Rhomb偏序集等一类广义Square偏序集的flag f和flag h向量的递归公式。
2. Stern偏序集的flag f和flag h向量
这部分我们主要研究了Stern偏序集的flag f和flag h向量。通过对Stern偏序集每一层的元素个数以及层与层之间的最大链个数进行归纳总结,得到定理2.1。
定理2.1令
并且
是Stern偏序集的秩数集,则
。
证明:
是秩为
层的元素个数,由图5易得
。
由
是秩为
层和秩为
层之间的最大链个数,而秩为
层每个元素到秩为
层均有
条最大链,即
条最大链,而秩为
层共有
个元素,故
。
公式对
成立,下面考虑
情况。
假设对
成立,则有
,任取
层,秩为
层每个元素到秩为
层均有
条最大链,即
条最大链,而前
层共有
个元素,故
。
通过定理2.1我们可以得到以下两个推论。
推论2.2 Stern偏序集从
(底部元素)到第n层的饱和链的个数为
。
推论2.3令
,则
。
现在我们应用flag f向量的公式得到flag h向量的公式。
定理2.4令
并且
是Stern偏序集的秩数集,则
.
证明:根据flag h向量的定义,
(2.1)
现在
的公式对
成立,我们对
进行归纳,即,
(2.2)
考虑从
到t的归纳步骤,根据flag h向量的定义,
我们希望证明,
(2.3)
这个定理源于,
为了证明(2.3),我们需要考虑以下两个事实:
事实2.5
(2.4)
(2.5)
证明(2.4),
接下来证明(2.5),
现在我们来证明(2.3),通过(2.4)很容易得到(2.3)对
成立。现在考虑
情况,通过重排(2.3)得到,
提取公因式
,我们剩下,
(2.6)
与(2.3)比较,我们只需要证明下列方程成立,
然后提取(2.6)中的系数
得到,
事实2.6
(2.7)
证明事实2.6:我们归纳
的情况,不难验证
是正确的。假设
是正确的,则,
因此,
这就完成了证明。
由以上结论得到推论2.7。
推论2.7令
,则
。
3. 结论
Stern偏序集的定义由R. Stanley给出,我们根据Stern偏序集的性质和结构特点对其flag f和flag h向量的公式进行归纳。并应用牟丽丽给出的Hexagonal偏序集的flag f和flag h向量公式的方法,给出了Stern偏序集的flag f和flag h向量的具体表达式。
文章引用
林佳倩. Stern偏序集的flag f和flag h向量的性质研究
The flag f and flag h Vectors of the Stern’s Poset[J]. 应用数学进展, 2021, 10(08): 2633-2638. https://doi.org/10.12677/AAM.2021.108273
参考文献
- 1. Rotr, C. (1964) On the Foundations of Combinatorial Theory I, Theory of Mobiousfunctions. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 2, 340-368. https://doi.org/10.1007/BF00531932
- 2. Stanley, R. (1997) Enumerative Combinatorics Vol. 1. Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9780511805967
- 3. Stanley, R. (2020) Some Linear Recurrences Motivated by Stern’s Diatomic Array. The American Mathematical Monthly, 127, 99-111. https://doi.org/10.1080/00029890.2020.1677104
- 4. Stanley, R. (2012) Enumerative Combinatorics. 2nd Edition, Vol. 1. Cambridge University Press, Cambridge.
- 5. Nyman, K. and Swartz, E. (2004) Inequalities for the h-Vectors and Flag h-Vectors of Geometric Lattices. Discrete & Computational Geometry, 32, 533-548. https://doi.org/10.1007/s00454-004-1137-z
- 6. Schweig, J. (2010) Convex-Ear Decompositions and the Flag H-Vector. Electronic Journal of Combinatorics, 18, 4.
https://doi.org/10.37236/491
- 7. Mu, L. (2020) Some Combinatorial Properties of Hexagonal Poset. Contributions to Discrete Mathematics, 15, 175-182.