International Journal of Mechanics Research
Vol.04 No.04(2015), Article ID:16383,5
pages
10.12677/IJM.2015.44009
Strain Energy Density of Generalized Stoney Model with Cylindrical Coordinate
Jia Li1*, Junjie Shi2, Huizhao Liu1
1School of Science, Hebei University of Technology, Tianjin
2State Key Laboratory for Artificial Microstructures and Mesoscopic Physics, Research Center for Wide-Gap Semiconductors, School of Physics, Peking University, Beijing
Received: Oct. 30th, 2015; accepted: Nov. 17th, 2015; published: Nov. 20th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The relation of strain-stress is an important aspect of understanding mechanical property of materials. According to it, we can further obtain the strain energy function of materials, and a series of other mechanical properties. The Stoney model is based on the relation of strain-stress of substrate, and the strain energy function is first obtained, and then the relation between stress in film and curvature is achieved. At the present case, we generalize the Stoney model, considering the strain and stress of z direction, and as well as shear strain related to z direction, and we obtain the strain energy function at any point with cylindrical coordinate. In addition, we obtain the integral expression of strain energy of system by considering of the in-plane uniform mismatch strain of the film.
Keywords:Strain and Stress, Mechanics, Stoney Model, Shear Strain, Strain Energy

柱坐标下推广的Stoney模型的应变能密度
李佳1*,史俊杰2,刘辉昭1
1河北工业大学理学院,天津
2北京大学物理学院,宽禁带半导体研究中心,人工微结构和介观物理国家重点实验室,北京

收稿日期:2015年10月30日;录用日期:2015年11月17日;发布日期:2015年11月20日

摘 要
材料的应力与应变关系是理解材料力学性能的重要方面,由此可以进一步得到材料的应变能函数,从而可以得到其它一系列力学特性。Stoney模型是从薄膜基底的应力应变关系出发,首先得到应变能函数,从而推得膜内应力与曲率的关系。这里,我们推广Stoney模型,考虑z方向的应力和应变,以及和z方向相关的剪切应变,得出柱坐标下的任意一点的应变能函数,并考虑膜内面间的均匀失配应变,得到体系的应变能的积分表达式。
关键词 :应力应变,力学,Stoney模型,剪切应变,应变能

1. 引言
关于薄膜材料的力学特性以及基底–膜异质体系的应力特征人们提出了很多模型加以研究,其中比较早的也是被大家普遍接受的为Stoney模型[1] 。1909年Stoney观察到金属薄膜沉积到厚的基底上会产生拉伸或者压缩,为了表达外延膜材料的剩余应力与基底的翘曲曲率之间的关系,基于圆盘形的基底–膜体系提出了此模型,它建立了膜的应力与体系曲率之间的关系,它基于以下几个基本假设:1) 外延膜的膜厚远小于基底厚度。2) 体系产生的应变足够小。3) 基底材料和膜材料是均匀各向同性的,满足弹性的线性特征。4) 沿厚度方向的所有应力分量是零。Stoney模型是研究膜–基底体系的应力特征较早的模型之一,其成功的建立了应力与曲率之间的联系,可以与实验上发展起来的曲率测量技术[2] 相结合有效的估算外延膜的剩余应力。但是,此模型只适用于薄膜,不能体现应力沿膜厚方向的演化特点,而且没有包含膜材料的具体特性,如弹性特征以及尺度等,所以得到的应力相当粗略。最重要的是,它并没有考虑z方向,即膜厚方向的应力(正应力和剪切应力),只能通过体系的曲率粗略的估算膜的面内应力[3] 。可是往往由于在膜的生长过程中不均匀的失配应变和热应变会产生剪切应力,进而影响其它力学特征。
在弹性体受外界作用而发生形变的过程中伴随着热量的交换,可以视为一个热力学过程,由所研究体系的特征并根据热力学第一定律可以得到体系的应变能函数,由此应变能函数可以进而推得其它力学量[4] 。Stoney模型的建立同样沿用了先得到应变能函数再通过函数取极值的方法得到应力。它在不考虑z方向应力应变以及剪切形变的情况下先得到体系的应力应变关系,然后推出体系的应变能函数,最终得到膜内应力与基底曲率之间的关系。实际上z方向的应力由于膜基底系统的形变也会存在,并且与z方向有关的剪切应变也不为零。因此,我们推广Stoney模型的结果,从膜的应力应变关系出发,考虑z方向应变和应力以及与其相关的剪切应变,建立柱坐标系,推导出体系的应变能函数。
2. 应变能函数
2.1. Stoney模型的应变能函数
根据胡克定律,分别计算三对正应力和三对剪切应力引起的应变,然后利用叠加原理和各向同性假设可以写出在直角坐标下的应力–应变关系(物理方程)为[4]
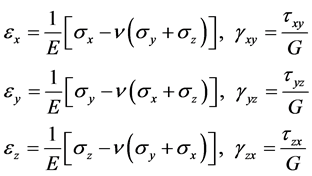 (1)
(1)
其中 ,
,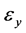 和
和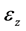 分别为x,y和z三个方向的应变,
分别为x,y和z三个方向的应变, ,
, 和
和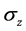 分别为x,y和z三个方向的应力。
分别为x,y和z三个方向的应力。 为泊松比,E为杨氏模量或弹性模量,G为剪切模量。
为泊松比,E为杨氏模量或弹性模量,G为剪切模量。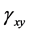 ,
,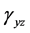 和
和 为三个剪切应变,
为三个剪切应变,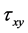 ,
, 和
和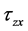 为与剪切应变对应的三个剪切应力。上式说明,体系中x,y和z三个方向的正应力与对应的正应变互相牵连,而剪切应力与应变之间没有牵连。期中G,
为与剪切应变对应的三个剪切应力。上式说明,体系中x,y和z三个方向的正应力与对应的正应变互相牵连,而剪切应力与应变之间没有牵连。期中G,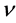 和E之间的关系为
和E之间的关系为
 (2)
(2)
因为柱坐标和直角坐标同为正交坐标,所以柱坐标系下的应力–应变关系与以上直角坐标的表达式类似,只需将应力和应变的脚标做相应更换即可,表达为如下
 (3)
(3)
其中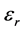 ,
, 和
和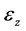 分别为r,
分别为r,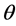 和z三个方向的应变,
和z三个方向的应变,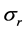 ,
,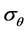 和
和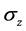 为r,
为r, 和z三个方向的应力。
和z三个方向的应力。 ,
,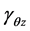 和
和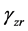 为三个方向的剪切应变,
为三个方向的剪切应变, ,
,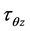 和
和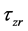 为与应变对应的三个方向的剪切应力。
为与应变对应的三个方向的剪切应力。 为泊松比,E为杨氏模量,G为剪切模量。
为泊松比,E为杨氏模量,G为剪切模量。
由(3)式可以解出应力的表示式,得到体系的应力与应变的弹性关系(拉梅式)为
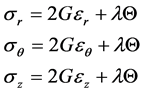 (4)
(4)
其中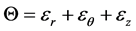 称为体积应变,
称为体积应变,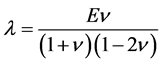 称为拉梅常数。
称为拉梅常数。
Stoney模型假设z方向应力为零,且不存在剪切应变,这样则(3)式则变为
 (5)
(5)
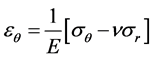 (6)
(6)
将(5)式和(6)式相加有
 (7)
(7)
其中 (体积应变),
(体积应变),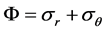 (体积应力)。
(体积应力)。
根据热力学第一定律:弹性体总能量的增加等于外力所做的功和传入热量的总和。由此出发可以推导出直角坐标下体系应变能函数的一般表达式为
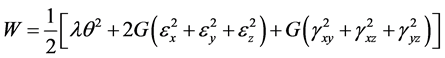 (8)
(8)
其中各个量的含义如前面所述,且可以保证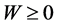 ,即单位体积的应变能恒为正值。
,即单位体积的应变能恒为正值。
按直角坐标与柱坐标之间的对应关系,在z方向应力为零且不存在剪切应力情况下,应变能函数的柱坐标系表示为
 (9)
(9)
以上推导用到了(2)式, 此即Stoney模型的应变能函数表达式。
2.2. Stoney模型应变能函数的推广
仍然沿用Stoney模型的推导思路,但是将其加以推广,考虑z方向的应变和应力,且与z方向相关的剪切应变相等且不为零,即 ,
,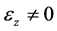 ,
, ,则体系的应力–应变关系为
,则体系的应力–应变关系为
 (10)
(10)
解出应力的表达式,可以得到如下弹性关系
 (11)
(11)
其中 ,
,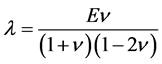 。
。
那么体系的单位体积的应变能,即应变能函数可以表达为
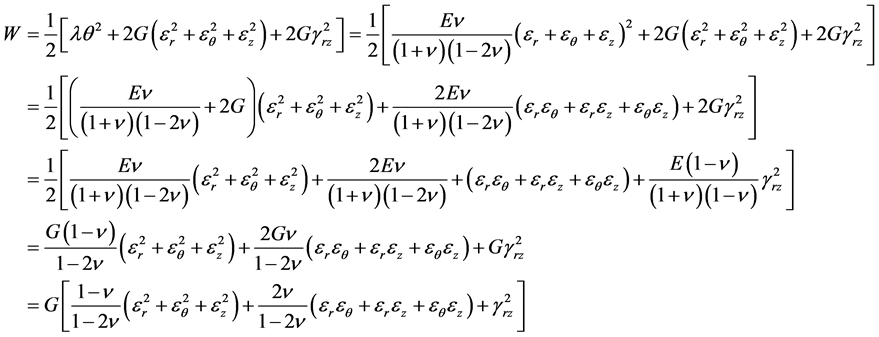 (12)
(12)
(12)式即为体系内任一点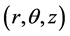 处的应变能密度。
处的应变能密度。
假设膜的面内应力相等,即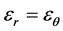 ,则(12)式变为
,则(12)式变为
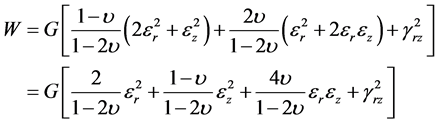 (13)
(13)
如果考虑膜内面间存在失配应变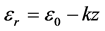 ,其中
,其中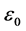 为常数,
为常数, 为曲率,则应变能函数(13)式变为
为曲率,则应变能函数(13)式变为
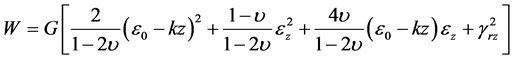 (14)
(14)
W的含义是膜内任意一点的应变能密度,即单位体积的应变能,如果想得到整个体系的应变能,则需要对整个体系进行积分。即表达为如下形式
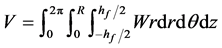
 (15)
(15)
3. 结论
我们沿用Stoney模型的建立思路,但是推广了Stoney模型,它不考虑z方向的正应力和应变以及与z相关的剪切应变。我们考虑z方向的应力和应变,并且考虑和z方向相关的剪切应变。在柱坐标下从体系的应力–应变关系出发,首先得到体系的弹性关系,然后推出体系在任意一点处的应变能函数,考虑膜内面间的均匀失配应变,得到了体系应变能的积分形式。在后续的研究中可以进一步按照Stoney模型类似取应变能极值的方法推出体系应力与曲率等参量之间的关系,建立推广后的Stoney模型。
基金项目
国家自然科学基金资助项目(No. 61204013, 11474012),河北省高等学校科学技术研究优秀青年基金资助项目(No. Y2012004)和河北省自然科学基金资助项目(No. E2014202189)。
文章引用
李 佳,史俊杰,刘辉昭. 柱坐标下推广的Stoney模型的应变能密度
Strain Energy Density of Generalized Stoney Model with Cylindrical Coordinate[J]. 力学研究, 2015, 04(04): 71-75. http://dx.doi.org/10.12677/IJM.2015.44009
参考文献 (References)
- 1. Stoney, G.G. (1909) The Tension of Metallic Films Deposited by Electrolysis. Proceedings of the Royal Society of London, 82, 172-175. http://dx.doi.org/10.1098/rspa.1909.0021
- 2. 李佳, 史俊杰, 吴洁君, 刘辉召, 齐浩然. GaN-蓝宝石异质厚膜体系界面应力特性研究[J]. 力学研究, 2014(3): 55-64.
- 3. Floro, J.A., Lucadamo, G.A., Chason, E., Freund, L.B., Sinclair, M., Twesten, R.D. and Hwang, R.Q. (1998) SiGe Island Shape Transitions Induced by Elastic Repulsion. Physical Review Letters, 80, 4717. http://dx.doi.org/10.1103/PhysRevLett.80.4717
- 4. 杨海波, 曹建国, 李洪波编著. 弹性与塑性力学简明交城[M]. 北京: 清华大学出版社, 2011.
NOTES
*通讯作者。