International Journal of Mechanics Research
Vol.
09
No.
01
(
2020
), Article ID:
34118
,
9
pages
10.12677/IJM.2020.91001
Creep Analysis of Viscoelastic Pavement under Interlayer Contact Condition
Xiang Chen, Hu Wang, Ya Wang
School of Science, Chang’an University, Xi’an Shaanxi

Received: Jan. 15th, 2020; accepted: Jan. 30th, 2020; published: Feb. 6th, 2020

ABSTRACT
In order to analyze the creep response of the viscoelastic pavement layer during interlayer contact, a finite element analysis model was established by simplifying the upper structure of the bridge, and the creep law of the pavement layer was analyzed under different load forms, different temperatures and different contact cohesion. The results show that the settlement displacement of asphalt layer under impact load is basically the same as that under vertical load, but it will produce large vertical uplift displacement, and its creep deformation is more complicated. The larger of the influence of loading time on creep of asphalt surface layer, and the higher the temperature, the greater the deformation, the faster the creep stability period; the temperature mainly affects the vertical ridge displacement of the surface layer, and the vertical bulge displacement increases with the increase of temperature, i.e. when the temperature is high, the unstable rut is more likely to occur; under the long-term loading of the impact load, when the cohesive force is 0.01 MPa, local slip occurs between the layers; when the cohesive force is greater than 0.01 MPa, the creep response of the asphalt surface layer remains the same.
Keywords:Bridge Deck Pavement, Interlayer Contact, Viscoelasticity, Creep, Finite Element Analysis

层间接触条件下粘弹性铺装层蠕变分析
陈翔,王虎,王雅
长安大学理学院,陕西 西安

收稿日期:2020年1月15日;录用日期:2020年1月30日;发布日期:2020年2月6日

摘 要
为了分析粘弹性铺装层在层间接触时的蠕变响应,以简化的桥梁上部结构为例建立了有限元分析模型,分析了在不同荷载形式、不同温度以及不同接触黏聚力下铺装层的蠕变规律。结果表明,冲击荷载作用下沥青层的沉降位移与竖直荷载作用下基本一致,但会产生较大的竖向隆起位移,其蠕变变形更加复杂;加载时间的长短对沥青面层蠕变影响较大,且温度越高,产生的变形越大,进入蠕变稳定期更快;温度主要对面层竖向隆起位移影响较大,其竖向隆起位移随着温度的升高而增大,即在高温时更易产生失稳型车辙;在冲击荷载的长时间加载下,当黏聚力为0.01 MPa时,层间会出现局部滑移;当黏聚力大于0.01 MPa时,沥青面层的蠕变响应保持不变。
关键词 :桥面铺装,层间接触,粘弹性,蠕变,有限元分析

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
沥青混合料是一种典型的黏弹性材料,其广泛应用于各型桥面的铺装层材料,因此,沥青铺装层也会表现出粘弹性特性。粘弹性铺装层的力学性能与铺装层的工作温度与受载时间息息相关,在高温条件下以及长时间荷载作用下,会产生显著的变形,且会伴随永久变形 [1] [2],永久变形会永久地损伤沥青铺装层的使用性能,且会危及行车安全,从而大大降低桥面铺装层的使用寿命。对于桥面铺装体系而言,层间通过粘聚力使得各层可良好完成力的传递,即层间接触的状态是否良好是影响铺装层受力的原因之一 [3]。
因此,本文基于现有的沥青混合料动态蠕变试验,通过prony级数转化为有限元软件ansys中的粘弹性参数,并对铺装层各层设置层间接触连接,分析了不同工况对粘弹性铺装层蠕变规律的影响,为沥青混合料在实际应用时提供一些参考模型。
2. 沥青的粘弹性模型
2.1. 基本理论
对于沥青路面层,常用的粘弹性模型有麦克斯韦模型、开尔文模型和伯格斯模型。在描述粘弹性材料时,麦克斯韦模型对于粘性变形表征较差。开尔文模型则在反映瞬态弹性变形方面不突出 [4];伯格斯模型是由麦克斯韦模型和开尔文模型组成的四元件粘弹性模型。可以比较蠕变方程,准确反映沥青混合料的瞬时弹性应变、纯粘性应变和粘弹性应变 [5] [6],其基本组成由图1所示。
Burgers模型的本构方程可写为
(1)
式中, ,,,。 分别为Maxwell模型的弹性模量、黏滞
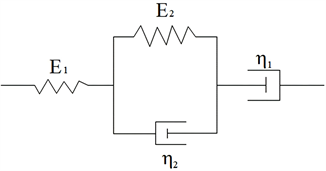
Figure 1. Burgers model
图1. Burgers模型
系数; 分别为Kelvin模型的弹性模量、黏滞系数; 分别为正应力、正应变对时间的一阶、二阶导数。
将Burgers模型通过拉式变换即可得出剪切松弛模量,然后再将得到的剪切松弛模量转化为prony级数后,便可实现有限元分析中材料参数的有效输入。AC-20的Burgers模型参数可根据文献 [7] 中的蠕变试验得到的结果选取,其具体数值如表1所示。
Table 1. Parameters of Burgers model of asphalt materials
表1. AC-20的Burgers模型参数
2.2. 参数转换
Burgers模型参数不能直接作为prony级数的输入量,需要将其转化为prony级数的剪切模量表达式中所对应的参数。由prony级数来表征粘弹性材料的属性时,其基本形式如下:
(2)
(3)
其中 和 为剪切模量, 是松弛时间。 为相对剪切模量, 为粘弹性材料的瞬时模量。
将式(1)中的Burgers模型弹性模量系数转化为剪切模量,转化的剪切模量表达式如式(4)所示,其各项参数表达式如式(5)所示。
根据文献 [8] 的研究结果,对式(1)进行Laplace变化,对其经过Laplace逆变换后即可得到剪切模量Prony级数表达式如式(6)所示。
(4)
(5)
(6)
由式(6)可以得出:
其中, ,。
通过Burgers模型转化成的prony级数参数中, 为相对剪切模量, 为松弛时间,沥青混合料的瞬时弹性模量、泊松比分别为 [9] [10]。具体的Burgers模型转换结果如表2所示。
Table 2. Prony series parameters for asphalt materials
表2. AC-20的Prony级数参数
3. 有限元模型建立
3.1. 层间接触设置
利用ANSYS有限元分析软件建立三维模型时,由于防水粘结层较薄,可以采用壳体单元Shell181进行仿真,其余采用三维八节点实体单元Solid185进行仿真。对于桥面和粘结层,粘结层和沥青铺装层均采用全接触建模,通过建立层间接触单元和目标单元来定义层间接触模式,接触单元和目标单元都使用三维面单位,两者成对出现。根据接触条件计算各层的力学响应时,层间剪切应力的传递满足库仑摩擦模型 [11] :
(7)
(8)
式中: 为极限剪应力; 为等效剪应力;P为法向接触压力;b为接触黏聚力,可通过试验获得; 为摩擦系数。
式(7)中,如果法向接触压力或摩擦系数为零,此时仍存在接触黏聚力,各层仍处于接触状态。当接触内聚力为零时,剪切应力仅通过层间摩擦传递。建立式(8)时,层间无滑移;当式(8)不成立时,层间发生相对滑移。
3.2. 模型参数及荷载布置
3.2.1. 模型参数
通过文献中的研究,考虑精度和计算效率,本文对计算模型进行了简化 [12],选取有限元模型平面尺寸为5 m × 5 m,混凝土板厚30 cm,防水层厚5 mm,沥青层厚5 cm。根据《混凝土结构设计规范》GB50010-2015 [13] 中的规定,本文对桥面板的弹性模量取为3 × 104 MPa,密度为2500 kg/m3,泊松比取0.20,沥青混凝土采用上一节得出的Prony级数粘弹性模型参数进行设置,密度取2360 kg/m3。由于粘结层材料属性不同于沥青混凝土,且本文分别分析了竖直荷载与冲击荷载对铺装层的蠕变响应规律,为更好的模拟其受力,粘结层单元可用正交各向异性单元进行模拟 [14],其材料参数如表3所示。
Table 3. Material parameters of waterproof adhesive layer
表3. 防水粘结层材料参数
3.2.2. 荷载布置
在对桥面铺装面层的蠕变规律分析中,计算模型的约束边界条件为上下表面自由,垂直于表面的四周完全固定。以汽车–超20车队550 kN重型车辆为计算车型。荷载类型为竖向静荷载和水平冲击荷载。加载面积0.6m × 0.2 m,加载时间5000 s。在模拟水平冲击载荷时,制动系数取0.5,水平制动力F与重力G的关系可以表示为:
(9)
载荷布置方式按照纵向使跨中产生最大弯矩布载,横向按照中载布置 [14],具体布载位置如图2所示,并对加载位置进行网格加密处理,以加大计算精度。
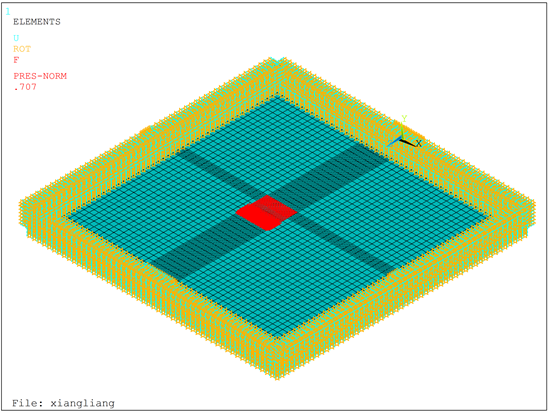
Figure 2. Finite element model
图2. 有限元模型
4. 铺装层蠕变规律分析
为了探讨桥面铺装层在层间接触条件下的受力情况,本文分析了多种工况,各种工况下的材料参数均按照前面文中的材料参数进行设置。并设置沥青层与粘结层间黏聚力为0.5 MPa,粘结层与桥面板间黏聚力为0.5 MPa。
4.1. 沥青面层在不同荷载下的变化响应
选取沥青面层沉降位移与鼓包位移最大值节点,分析其在冲击荷载与竖直荷载作用下的位移时程曲线如图3所示。由图3可知,随着时间的增长,两处节点的位移均有所增加。竖直荷载与冲击荷载作用下的沉降位移基本一致,但冲击荷载作用下的鼓包位移显然较大,且其增长幅度也较高。由上述分析可知,随着荷载作用时间的增长,两种荷载作用下沥青面层的竖向位移均有所增加,但由于冲击荷载还伴随着水平冲击力,因此,其鼓包位移也较为显著,除产生结构型车辙外,还会由于水平冲击力的影响,使得沥青面层剪应力过大产生失稳型车辙。因此,本文主要研究冲击荷载作用下沥青铺装层的蠕变响应。

Figure 3. Time history curve of extreme point displacement under different loads
图3. 不同荷载下极值点位移时程曲线
4.2. 沥青层蠕变随时间变化
选取竖向位移极值点,分析在冲击荷载下其随温度变化的位移时程曲线如图4、图5所示。由图4、图5可以看出,在三种温度条件下,沥青面层的蠕变变形均会经历蠕变迁移期与蠕变稳定期,在蠕变稳定期,沥青面层位移时程曲线基本呈线性,即沥青面层蠕变位移随着时间的增加表现出线性增长趋势。在加载时长5000 s内,沥青面层并未产生蠕变破坏。随着时间的增长,沥青面层的蠕变位移逐渐变大,且在60℃时,其对应的位移更大,也会更早进入蠕变稳定期。由上述分析可知,加载时间的长短对沥青面层蠕变影响较大,沥青面层经受长时间荷载累积后,便会产生永久性变形;温度越高,产生的蠕变变形越大,进入蠕变稳定期更快,更易产生永久变形。
4.3. 沥青层蠕变随温度变化
选取沥青面层表面横向中截面与纵向中截面节点,在加载时长为5000 s时,对其在不同温度下的竖向位移进行分析如图6、图7所示。由图6可知,在荷载作用边缘沉降位移最大,在荷载作用周围会产生竖向隆起,且在60℃时产生最大沉降位移;由图7可知,在冲击荷载作用下,由于存在水平冲击力,
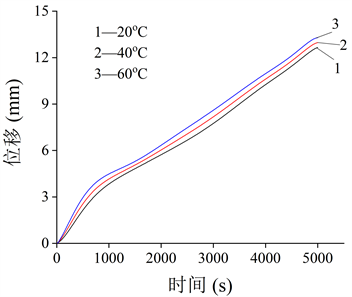
Figure 4. Time history curve of bulged displacement of asphalt surface layer
图4. 沥青面层鼓包位移时程曲线
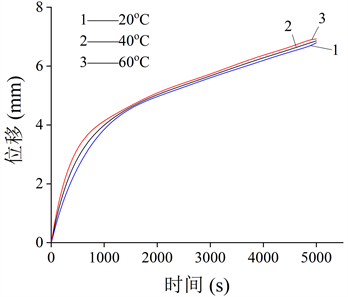
Figure 5. Settlement displacement time history curve of asphalt surface layer
图5. 沥青面层沉降位移时程曲线

Figure 6. Lateral joint displacement at different temperatures
图6. 不同温度下横向节点位移
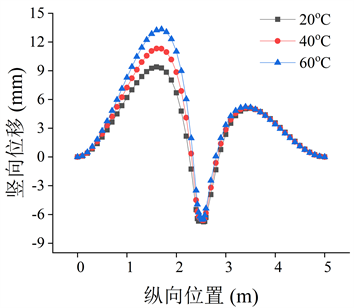
Figure 7. Displacement of longitudinal joints at different temperatures
图7. 不同温度下纵向节点位移
会在荷载作用区域的行车方向周围产生较大的竖向隆起位移,且会随着温度的升高而增大,其增长幅度相比于沉降位移的增长幅度也较大。由上述分析可以得知,在冲击荷载作用下,会在荷载作用区的行车方向周围产生较大竖向位移,且温度对其的影响较大,即高温时更易出现失稳型车辙。
4.4. 沥青层蠕变随层间粘聚力变化
选取加载时长5000 s时竖向位移极值点,分析其在不同黏聚力时的蠕变响应如表4所示。由表4可知,当黏聚力大于0.01 MPa时,其竖向位移与接触摩擦应力基本保持不变;当黏聚力为0.01 MPa时,其鼓包位移与沉降位移均略有减小,而接触摩擦应力均略有增加。由上述分析可知,当黏聚力为0.01 MPa时,在冲击荷载的长时加载下,层间出现部分滑移;当黏聚力大于0.01 MPa时,其力学响应保持不变。
Table 4. Creep response under different cohesion forces
表4. 不同黏聚力下的蠕变响应
5. 结论
本文结合有限元分析软件,设定了层间接触条件,分析了粘弹性铺装层在不同荷载形式、温度以及黏聚力下的蠕变响应,得出结论如下:
1) 在冲击荷载与竖直荷载的长时间作用下,沥青层的蠕变变形略有不同,冲击荷载下会使得沥青层剪应力过大而产生较大的竖向隆起位移,其产生的变形更为复杂。
2) 加载时间的长短对沥青面层蠕变影响较大,沥青面层经受长时间荷载累积后,便会产生永久性变形;温度越高,产生的蠕变变形越大,进入蠕变稳定期更快,更易产生永久变形。
3) 在冲击荷载作用下,会在荷载作用区的行车方向周围产生较大竖向位移,且温度对其的影响较大,即高温时更易出现失稳型车辙。
4) 当黏聚力为0.01 MPa时,在冲击荷载的长时间加载下,层间出现部分滑移;当黏聚力大于0.01 MPa时,其力学响应保持不变。
综上结论可以得出,冲击荷载不仅会在荷载区域产生沉降位移,还会使沥青层剪应力过大从而在行车方向附近产生较大的竖向隆起变形,其对沥青层蠕变响应的影响较大;温度对沥青层的蠕变响应的影响较为明显,温度越高,沥青层的蠕变更明显;层间接触粘聚力为0.01 MPa是一个临界值,当大于0.01 MPa时,层间接触良好。
基金项目
国家自然科学科学基金资助项目(No. 11702033)。
文章引用
陈 翔,王 虎,王 雅. 层间接触条件下粘弹性铺装层蠕变分析
Creep Analysis of Viscoelastic Pavement under Interlayer Contact Condition[J]. 力学研究, 2020, 09(01): 1-9. https://doi.org/10.12677/IJM.2020.91001
参考文献
- 1. 侯曙光. 基于动态蠕变试验的沥青混合料黏弹性分析[J]. 南京工业大学学报(自然科学版), 2010, 32(1): 33-36.
- 2. 董满生, 鹿婧, 凌天清, 等. 考虑温度效应的沥青混合料参数模型[J]. 工程力学, 2016, 33(6): 180-185, 193.
- 3. 万晨光, 申爱琴, 郭寅川, 等. 层间接触状态对桥面铺装结构力学响应的影响[J]. 江苏大学学报(自然科学版), 2016, 37(2): 236-241.
- 4. 汪凡. 基于流变学本构模型和动力有限元分析的沥青路面车辙计算[D]: [硕士学位论文]. 重庆: 重庆交通大学, 2009.
- 5. 叶青. 基于粘弹性的沥青混合料疲劳性能研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2016.
- 6. 曹卫锋, 吕彭民. 粘弹性沥青路面车辆动力响应仿真分析研究[J]. 计算机仿真, 2013, 30(4): 173-177.
- 7. 龙尧, 谢晶, 王德群, 等. 基于Burgers模型的沥青混合料室内车辙试验粘弹性分析[J]. 中外公路, 2011, 31(5): 239-242.
- 8. 陈静云, 周长红, 王哲人. 沥青混合料蠕变试验数据处理与粘弹性计算[J]. 东南大学学报(自然科学版), 2007, 37(6): 1091-1095.
- 9. 王琨, 郝培文. 沥青高温蠕变变形的粘弹性组成研究[J]. 公路工程, 2017, 42(5): 122-126, 172.
- 10. 潘晓明, 余俊, 杨钊, 等. 一种将线性粘弹微分型本构方程应用到ABAQUS的方法[J]. 华侨大学学报(自然科学版), 2010, 31(5): 570-575.
- 11. 王勋涛, 封建湖, 王虎. 层间接触时空心板桥铺装层应力分析[J]. 公路, 2017, 62(6): 14-22.
- 12. 陈渊召. 沥青混合料桥面铺装新技术研究[M]. 北京: 中国水利水电出版社, 2016: 23-24.
- 13. 中国建筑科学研究院. 混凝土结构设计规范GB50010-2015[S]. 北京: 中国建筑科学研究院, 2015.
- 14. 胡钢. 层间接触状态对路面结构力学响应的影响[J]. 公路, 2015, 60(3): 34-40.
