正交异性材料I + II + III混合型裂纹尖端应力分析 Crack-Tip Stress Analysis for Orthotropic Materials under Mixed-Mode I + II + III Loading

doi:10.12677/IJM.2020.94014

International Journal of Mechanics Research
Vol. 09 No. 04 ( 2020 ), Article ID: 39016 , 12 pages
10.12677/IJM.2020.94014

正交异性材料I + II + III混合型裂纹尖端应力分析

贾普荣

●How to Cite this Article

西北工业大学力学与土木建筑学院，陕西西安

收稿日期：2020年11月13日；录用日期：2020年11月30日；发布日期：2020年12月7日

摘要

大多数工程材料显示出脆性特征(例如，复合材料)，而脆性材料中的裂纹已公认为是工程结构破坏的主要原因，裂纹尖端应力场必然是建立断裂判据的基础。因此，本文重点讨论I + II + III混合型加载下的裂纹尖端应力，采用线弹性力学方法解决正交异性材料典型应力边值问题。首先确定三维空间问题的弹性力学基本方程，基于复变函数理论求解控制方程。接着利用应力函数和坐标变换求解基本方程。最终获得了混合型加载下正交异性材料裂纹尖端附近的应力分量通解。

关键词

正交异性材料，裂纹尖端应力，弹性力学，复变函数，混合型加载

Crack-Tip Stress Analysis for Orthotropic Materials under Mixed-Mode I + II + III Loading

Purong Jia

School of Mechanics and Civil Engineering & Architecture, Northwestern Polytechnical University, Xi’an, Shaanxi

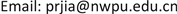
Received: Nov. 13^th, 2020; accepted: Nov. 30^th, 2020; published: Dec. 7^th, 2020

ABSTRACT

Most engineering materials exhibit brittle behavior, such as composites. The main cause for failures of engineering structures has been generally recognized to be the cracks in brittle materials. The crack-tip stress field must be the basis for establishing fracture criteria. So this paper will focus the discussion on crack-tip stresses under mixed mode I + II + III loading. Typical stress boundary problem for the orthotropic materials is considered to be solved by the method of linear elastic mechanics. First, the basic equations of elastic mechanics are determined for three-dimensional space problems, and the governing equations are solved based on the theory of complex variable function. Second, the basic equations are solved by using the stress functions and the coordinate transformation. And finally, the general solutions of stress components near the crack-tip are derived for the orthotropic materials under mixed mode loading.

Keywords:Orthotropic Materials, Crack-Tip Stress, Elastic Mechanics, Complex Variable Function, Mixed Mode Loading

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

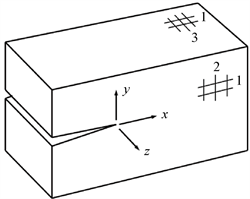
一般脆性材料结构中包含着裂纹，这是导致结构发生低应力脆性断裂的根源。线弹性断裂力学的建立与发展为研究脆性材料裂纹尖端力学特性及裂纹扩展规律奠定了理论基础，尤其是采用应力强度因子作为描述裂纹扩展的关键参数在工程结构强度分析中得到广泛应用。断裂力学的理论基础就是利用弹性力学方法阐述裂纹尖端应力场及位移场，按照裂纹的受力特点和变形状态把裂纹划分为3种基本类型：张开型、滑移型、撕开型(或称I型、II型、III型) [1] [2] [3]。工程材料中的裂纹区域常会发生复杂变形状态，因而出现(I + II + III)混合型的裂纹问题，在断裂力学书籍中已有详细的理论介绍。随着先进复合材料的工程应用日益扩张，各向异性材料断裂力学的理论发展显得更加突出。复合材料通常呈现出脆性特点，其断裂力学研究仍以弹性力学为基础。早在半个世纪前，力学家已推广复变函数法解决各向异性材料弹性力学问题，其求解方法为复合材料断裂力学奠定了理论基础 [4] [5] [6]。利用复变函数方法在解决复合材料应力边值问题中已取得显著结果，且理论和应用研究不断增加 [7] [8] [9]。本文针对正交异性材料混合型裂纹(I + II + III型)问题开展研究(如图1所示)，推导出典型正交异性材料裂纹端部应力场的通解，并确定出应力分量与材料特征参数的关系。

Figure 1. Orthotropic body with a crack

图1. 含裂纹正交异性体

2. 弹性力学基本理论

常见的承载结构力学分析都可归结为求解应力边值问题，必须研究结构内部复杂应力分布。按照数学推理求解弹性力学问题主要从三个方面考虑：静力学、几何学和物理学。为了便于讨论混合型裂纹尖端应力，先列出弹性力学的基本方程。对于空间结构体内各点应力状态(忽略体积力)，可建立静力平衡偏微分方程为：

$\begin{array}{l} \frac{\partial σ_{x}}{\partial x} + \frac{\partial τ_{x y}}{\partial y} + \frac{\partial τ_{x z}}{\partial z} = 0 \\ \frac{\partial τ_{x y}}{\partial x} + \frac{\partial σ_{y}}{\partial y} + \frac{\partial τ_{y z}}{\partial z} = 0 \\ \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} + \frac{\partial σ_{z}}{\partial z} = 0 \end{array}}$ (1)

结构受力后发生变形，各点沿坐标轴 $(x, y, z)$ 方向的位移用 $(u_{1}, u_{2}, u_{3})$ 表示。三维弹性体内的应变与位移分量的变化率相关，根据几何关系可得以下方程：

$\begin{array}{l} ε_{x} = \frac{\partial u_{1}}{\partial x}, ε_{y} = \frac{\partial u_{2}}{\partial y}, ε_{z} = \frac{\partial u_{3}}{\partial z} \\ γ_{y z} = \frac{\partial u_{2}}{\partial z} + \frac{\partial u_{3}}{\partial y}, γ_{x z} = \frac{\partial u_{1}}{\partial z} + \frac{\partial u_{3}}{\partial x}, γ_{x y} = \frac{\partial u_{1}}{\partial y} + \frac{\partial u_{2}}{\partial x} \end{array}}$ (2)

正交异性材料广泛应用于工程结构中，材料物理特性非常突出，共有九个独立的弹性常数。选择空间坐标轴 $(x, y, z)$ 与材料主方向一致，则确定的物理方程为：

$\begin{array}{l} σ_{x} = C_{11} ε_{x} + C_{12} ε_{y} + C_{13} ε_{z}, τ_{y z} = C_{44} γ_{y z} \\ σ_{y} = C_{12} ε_{x} + C_{22} ε_{y} + C_{23} ε_{z}, τ_{x z} = C_{55} γ_{x z} \\ σ_{z} = C_{13} ε_{x} + C_{23} ε_{y} + C_{33} ε_{z}, τ_{x y} = C_{66} γ_{x y} \end{array}}$ (3)

这是用刚度系数 $C_{i j}$ 表示的应力与应变关系。若采用柔度系数 $S_{i j}$ 表示材料应变与应力关系，则三维正交异性材料的本构方程为：

$\begin{array}{l} ε_{x} = S_{11} σ_{x} + S_{12} σ_{y} + S_{13} σ_{z}, γ_{y z} = S_{44} τ_{y z} \\ ε_{y} = S_{12} σ_{x} + S_{22} σ_{y} + S_{23} σ_{z}, γ_{x z} = S_{55} τ_{x z} \\ ε_{z} = S_{13} σ_{x} + S_{23} σ_{y} + S_{33} σ_{z}, γ_{x y} = S_{66} τ_{x y} \end{array}}$ (4)

式中柔度系数 $S_{i j}$ 与工程弹性常数的关系为：

$\begin{array}{l} S_{11} = \frac{1}{E_{1}}, S_{12} = - \frac{μ_{12}}{E_{1}} = - \frac{μ_{21}}{E_{2}}, S_{44} = \frac{1}{G_{23}} \\ S_{22} = \frac{1}{E_{2}}, S_{13} = - \frac{μ_{13}}{E_{1}} = - \frac{μ_{31}}{E_{3}}, S_{55} = \frac{1}{G_{13}} \\ S_{33} = \frac{1}{E_{3}}, S_{23} = - \frac{μ_{23}}{E_{2}} = - \frac{μ_{32}}{E_{3}}, S_{66} = \frac{1}{G_{12}} \end{array}}$ (5)

在讨论含裂纹弹性体变形时，通常将坐标轴y选为裂纹面的法线方向，即裂纹面平行于坐标x-z平面，如图1所示。正交异性体主方向1-2-3分别与坐标轴x-y-z平行。当弹性体受力时，体内各点发生相对位移，选用 $u_{1}, u_{2}, u_{3}$ 分别表示沿 $x, y, z$ 方向的位移。设裂纹尖端区域各点的位移分量都不随z变化，只是x, y的函数，即有：

$u_{1} = u_{1} (x, y), u_{2} = u_{2} (x, y), u_{3} = u_{3} (x, y)$

根据几何方程(2)和设定的位移函数，应变分量简化为：

$\begin{array}{l} ε_{x} = \frac{\partial u_{1}}{\partial x}, ε_{y} = \frac{\partial u_{2}}{\partial y}, ε_{z} = 0 \\ γ_{y z} = \frac{\partial u_{3}}{\partial y}, γ_{x z} = \frac{\partial u_{3}}{\partial x}, γ_{x y} = \frac{\partial u_{1}}{\partial y} + \frac{\partial u_{2}}{\partial x} \end{array}}$ (6)

显然，应变分量都不随z变化， $ε_{i j} = ε_{i j} (x, y)$ 。再由材料的物理方程(3)可知，应力分量也只是x，y的函数， $σ_{i j} = σ_{i j} (x, y)$ 。按照简化后的几何方程(6)，可推导出有效的变形协调方程具有以下两种形式：

$\begin{array}{l} \frac{\partial^{2} ε_{x}}{\partial y^{2}} + \frac{\partial^{2} ε_{y}}{\partial x^{2}} = \frac{\partial^{2} γ_{x y}}{\partial x \partial y} \\ \frac{\partial γ_{x z}}{\partial y} = \frac{\partial γ_{y z}}{\partial x} \end{array}}$ (7)

由于应力分量都不随z变化，平衡方程(1)可简化为：

$\frac{\partial σ_{x}}{\partial x} + \frac{\partial τ_{x y}}{\partial y} = 0, \frac{\partial τ_{x y}}{\partial x} + \frac{\partial σ_{y}}{\partial y} = 0, \frac{\partial τ_{x z}}{\partial x} + \frac{\partial τ_{y z}}{\partial y} = 0$ (8)

简化的平衡方程中缺少应力分量 $σ_{z}$ ，说明在此种情形下 $σ_{z}$ 不重要，可以忽略。为了后面分析方便，可设 $σ_{z} \approx 0$ ，在裂纹端部应力分析时 $σ_{z}$ 就不必考虑了。因此，沿z方向的正应力和正应变通常较小，都可被略去，以便使实际问题分析得以简化。

关于裂纹体的变形和应力分析，重点放在裂纹端部区域，因此将坐标系建立在裂纹尖端处(如图2所示)。将z轴沿裂纹尖端放置，x轴指向裂纹前沿，y轴为裂纹面的法线方向。在x-o-y平面内建立极坐标系 $o r θ$ ，两类坐标系的变换关系为：

$x = r \cos θ, y = r \sin θ$ (9)

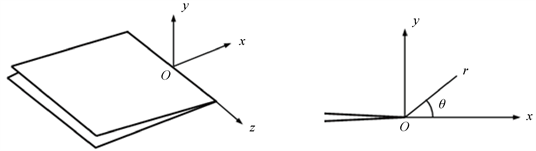
Figure 2. Crack-tip zone and coordinate system

图2. 裂纹端部区及坐标系

根据平衡方程(8)的特点，选取与z无关的应力函数 $F_{12} = F_{12} (x, y)$ ， $F_{3} = F_{3} (x, y)$ 进行偏微分方程的求解。首先采用应力函数把应力分量表示如下：

$σ_{x} = \frac{\partial^{2} F_{12}}{\partial y^{2}}, σ_{y} = \frac{\partial^{2} F_{12}}{\partial x^{2}}, τ_{x y} = - \frac{\partial^{2} F_{12}}{\partial x \partial y}, τ_{y z} = \frac{\partial F_{3}}{\partial x}, τ_{x z} = - \frac{\partial F_{3}}{\partial y}$ (10)

平衡方程(8)自动满足。把应力分量表达式(10)代入本构方程(4)，并令 $σ_{z} = 0$ ，就可将应变分量用应力函数表示为：

$\begin{array}{l} ε_{x} = S_{11} \frac{\partial^{2} F_{12}}{\partial y^{2}} + S_{12} \frac{\partial^{2} F_{12}}{\partial x^{2}}, ε_{y} = S_{12} \frac{\partial^{2} F_{12}}{\partial y^{2}} + S_{22} \frac{\partial^{2} F_{12}}{\partial x^{2}} \\ γ_{x y} = - S_{66} \frac{\partial^{2} F_{12}}{\partial x \partial y}, γ_{y z} = S_{44} \frac{\partial F_{3}}{\partial x}, γ_{x z} = - S_{55} \frac{\partial F_{3}}{\partial y} \end{array}}$ (11)

再将应变分量代入变形协调方程(7)，可得到以应力函数表示的偏微分方程，也就是解决正交异性材料混合型裂纹尖端场的基本方程。推得的两类偏微分方程为：

$\begin{array}{l} \frac{\partial^{4} F_{12}}{\partial y^{4}} + 2 B_{1} \frac{\partial^{4} F_{12}}{\partial x^{2} \partial y^{2}} + B_{2} \frac{\partial^{4} F_{12}}{\partial x^{4}} = 0 \\ \frac{\partial^{2} F_{3}}{\partial y^{2}} + B_{3} \frac{\partial^{2} F_{3}}{\partial x^{2}} = 0 \end{array}}$ (12)

式中系数与材料弹性常数有关，按下式确定：

$B_{1} = \frac{S_{66}}{2 S_{11}} + \frac{S_{12}}{S_{11}} = \frac{E_{1}}{2 G_{12}} - μ_{12}, B_{2} = \frac{S_{22}}{S_{11}} = \frac{E_{1}}{E_{2}}, B_{3} = \frac{S_{44}}{S_{55}} = \frac{G_{13}}{G_{23}}$ (13)

显然，用应力函数 $F_{12}$ 和 $F_{3}$ 表示的两类变形协调方程是相互独立的，可分开求解。

3. 混合型裂纹尖端场的复变函数解法

在解决弹性力学边值问题时，利用复变函数及其坐标变换法得到了一些经典的结果，若采用实函数求解就十分困难。为了解决复合材料中的应力边值问题，引入一个复变量w，并用直角坐标和极坐标表示为：

$\begin{array}{l} w = x + i h y = r \cos θ + i h r \sin θ = r (\cos θ + i h \sin θ) \\ \bar{w} = x - i h y = r \cos θ - i h r \sin θ = r (\cos θ - i h \sin θ) \end{array}}$ (14)

式中系数h取为实常数(且令： $h > 0$ )。由直角坐标求导法则可得偏导数公式：

$\frac{\partial w}{\partial x} = \frac{\partial \bar{w}}{\partial x} = 1, \frac{\partial w}{\partial y} = - \frac{\partial \bar{w}}{\partial y} = i h$ (15)

实变函数 $F (x, y)$ 的偏导数可用含复变量的函数 $F [w (x, y), \bar{w} (x, y)]$ 表示为：

$\begin{array}{l} \frac{\partial F}{\partial x} = \frac{\partial F}{\partial w} \frac{\partial w}{\partial x} + \frac{\partial F}{\partial \bar{w}} \frac{\partial \bar{w}}{\partial x} = \frac{\partial F}{\partial w} + \frac{\partial F}{\partial \bar{w}} \\ \frac{\partial F}{\partial y} = \frac{\partial F}{\partial w} \frac{\partial w}{\partial y} + \frac{\partial F}{\partial \bar{w}} \frac{\partial \bar{w}}{\partial y} = i h (\frac{\partial F}{\partial w} - \frac{\partial F}{\partial \bar{w}}) \end{array}}$ (16)

进一步可求得以下二阶偏导数关系：

$\begin{array}{l} \frac{\partial^{2} F}{\partial x^{2}} = (\frac{\partial}{\partial w} + \frac{\partial}{\partial \bar{w}}) (\frac{\partial F}{\partial w} + \frac{\partial F}{\partial \bar{w}}) = \frac{\partial^{2} F}{\partial w^{2}} + 2 \frac{\partial^{2} F}{\partial w \partial \bar{w}} + \frac{\partial^{2} F}{\partial {\bar{w}}^{2}} \\ \frac{\partial^{2} F}{\partial x \partial y} = i h (\frac{\partial}{\partial w} + \frac{\partial}{\partial \bar{w}}) (\frac{\partial F}{\partial w} - \frac{\partial F}{\partial \bar{w}}) = i h (\frac{\partial^{2} F}{\partial w^{2}} - \frac{\partial^{2} F}{\partial {\bar{w}}^{2}}) \\ \frac{\partial^{2} F}{\partial y^{2}} = - h^{2} (\frac{\partial}{\partial w} - \frac{\partial}{\partial \bar{w}}) (\frac{\partial F}{\partial w} - \frac{\partial F}{\partial \bar{w}}) = - h^{2} (\frac{\partial^{2} F}{\partial w^{2}} - 2 \frac{\partial^{2} F}{\partial w \partial \bar{w}} + \frac{\partial^{2} F}{\partial {\bar{w}}^{2}}) \end{array}}$ (17)

利用以上偏导数变换式可将偏微分方程(12)转化为：

$\begin{array}{l} (h^{4} - 2 B_{1} h^{2} + B_{2}) (\frac{\partial^{4} F_{12}}{\partial w^{4}} + \frac{\partial^{4} F_{12}}{\partial {\bar{w}}^{4}}) + 4 (B_{2} - h^{4}) (\frac{\partial^{4} F_{12}}{\partial w^{3} \partial \bar{w}} + \frac{\partial^{4} F_{12}}{\partial w \partial {\bar{w}}^{3}}) \\ + 2 (3 h^{4} + 2 B_{1} h^{2} + 3 B_{2}) \frac{\partial^{4} F_{12}}{\partial w^{2} \partial {\bar{w}}^{2}} = 0 \end{array}$ (18)

$(B_{3} - h_{3}^{2}) (\frac{\partial^{2} F_{3}}{\partial w_{3} \partial w_{3}} + \frac{\partial^{2} F_{3}}{\partial {\bar{w}}_{3} \partial {\bar{w}}_{3}}) + 2 (B_{3} + h_{3}^{2}) \frac{\partial^{2} F_{3}}{\partial w_{3} \partial {\bar{w}}_{3}} = 0$ (19)

式中， $w_{3} = x + i h_{3} y$ ， ${\bar{w}}_{3} = x - i h_{3} y$ ， $F_{3} = F_{3} (x, y) = F_{3} (w_{3}, {\bar{w}}_{3})$ 。由于方程(18)比较复杂，放在后边详细讨论，首先对二阶偏微分方程(19)进行解答。

二阶偏微分方程(19)的前项系数可以等于零，而后项系数大于零。因此，可将微分方程转化为一个材料参数方程和一个特殊的偏微分方程：

$B_{3} - h_{3}^{2} = 0, \frac{\partial^{2} F_{3}}{\partial w_{3} \partial {\bar{w}}_{3}} = 0$

再根据式(13)的常数定义，待定参数 $h_{3}$ 可确定为：

$h_{3} = \sqrt{B_{3}} = \sqrt{\frac{G_{13}}{G_{23}}}$ (20)

为满足偏微分方程，应力函数 $F_{3}$ 可用复变函数表示为：

$F_{3} = A_{3} Φ_{3} (w_{3}) + A_{3} {\bar{Φ}}_{3} ({\bar{w}}_{3}) = A_{3} Φ_{3} (w_{3}) + A_{3} \bar{Φ_{3} (w_{3})} = 2 A_{3} Re Φ_{3}$ (21)

式中 $A_{3}$ 是待定实常数，再由偏导数法则可求得：

$\frac{\partial F_{3}}{\partial x} = \frac{\partial F_{3}}{\partial w_{3}} + \frac{\partial F_{3}}{\partial {\bar{w}}_{3}} = A_{3} ({Φ^{'}}_{3} + {\bar{Φ}}^{'}_{3}), \frac{\partial F_{3}}{\partial y} = i h_{3} (\frac{\partial F_{3}}{\partial w_{3}} - \frac{\partial F_{3}}{\partial {\bar{w}}_{3}}) = A_{3} h_{3} i ({Φ^{'}}_{3} - {\bar{Φ}}^{'}_{3})$

将两个偏导数表达式代入到式(10)，可得两个应力分量的复变函数表达式：

$\begin{array}{l} τ_{y z} = A_{3} ({Φ^{'}}_{3} + {\bar{Φ}}^{'}_{3}) = 2 A_{3} Re {Φ^{'}}_{3} \\ τ_{x z} = - A_{3} h_{3} i ({Φ^{'}}_{3} - {\bar{Φ}}^{'}_{3}) = 2 A_{3} h_{3} Im {Φ^{'}}_{3} \end{array}}$ (22)

下面对方程(18)进行解答。

四阶偏微分方程(18)由三大项组成，前两项系数可以等于零，而第三项系数大于零。因此，可将微分方程转化为不同的材料参数方程和特殊的偏微分方程，下面主要按两种情形分别讨论应力函数的复变函数表达式。

情形1：令 $h^{4} - 2 B_{1} h^{2} + B_{2} = 0$ ， $B_{2} - h^{4} = 0$ ， $\frac{\partial^{4} F_{12}}{\partial w^{2} \partial {\bar{w}}^{2}} = 0$

显然参数h具有限定解答为： $h^{4} = B_{2} = B_{1}^{2}$ 。因前面已设定 $h > 0$ ，并由式(13)确定的弹性常数，可将h用工程弹性常数表示为：

$h = \sqrt{\frac{E_{1}}{2 G_{12}} - μ_{12}} = \sqrt[4]{\frac{E_{1}}{E_{2}}}$ (23)

再由 $\frac{\partial^{4} F_{12}}{\partial w^{2} \partial {\bar{w}}^{2}} = 0$ 确定出应力函数 $F_{12}$ 用复变函数表示的一般公式为：

$\begin{matrix} F_{12} = (C_{1} + i C_{2}) Ψ + (C_{1} - i C_{2}) \bar{Ψ} + (C_{3} + i C_{4}) \bar{w} Φ + (C_{3} - i C_{4}) w \bar{Φ} \\ = 2 C_{1} Re Ψ - 2 C_{2} Im Ψ + 2 C_{3} Re (\bar{w} Φ) - 2 C_{4} Im (\bar{w} Φ) \end{matrix}$ (24)

式中，复变函数记为： $Ψ = Ψ (w)$ ， $\bar{Ψ} = \bar{Ψ} (\bar{w})$ ， $Φ = Φ (w)$ ， $\bar{Φ} = \bar{Φ} (\bar{w})$ 。根据具体问题可适当选取复变函数类型，复变量 $w, \bar{w}$ 由式(14)给定。

由偏导数法则可求出应力函数 $F_{12}$ 的各个偏导数为：

$\frac{\partial F_{12}}{\partial w} = (C_{1} + i C_{2}) Ψ^{'} + (C_{3} + i C_{4}) \bar{w} Φ^{'} + (C_{3} - i C_{4}) \bar{Φ}$

$\frac{\partial F_{12}}{\partial \bar{w}} = (C_{1} - i C_{2}) {\bar{Ψ}}^{'} + (C_{3} + i C_{4}) Φ + (C_{3} - i C_{4}) w {\bar{Φ}}^{'}$

$\frac{\partial^{2} F_{12}}{\partial w^{2}} = (C_{1} + i C_{2}) Ψ^{″} + (C_{3} + i C_{4}) \bar{w} Φ^{″}$

$\frac{\partial^{2} F_{12}}{\partial {\bar{w}}^{2}} = (C_{1} - i C_{2}) {\bar{Ψ}}^{″} + (C_{3} - i C_{4}) w {\bar{Φ}}^{″}$

$\frac{\partial^{2} F_{12}}{\partial w \partial \bar{w}} = (C_{3} + i C_{4}) Φ^{'} + (C_{3} - i C_{4}) {\bar{Φ}}^{'}$

将二阶偏导数表达式代入式(17)，并按照式(10)确定出应力分量为：

$\begin{array}{l} σ_{x} = - h^{2} [C_{1} (Ψ^{″} + {\bar{Ψ}}^{″}) + i C_{2} (Ψ^{″} - {\bar{Ψ}}^{″}) - 2 C_{3} (Φ^{'} + {\bar{Φ}}^{'}) - 2 i C_{4} (Φ^{'} - {\bar{Φ}}^{'}) \\ + C_{3} (\bar{w} Φ^{″} + w {\bar{Φ}}^{″}) + i C_{4} (\bar{w} Φ^{″} - w {\bar{Φ}}^{″})] \\ σ_{y} = C_{1} (Ψ^{″} + {\bar{Ψ}}^{″}) + i C_{2} (Ψ^{″} - {\bar{Ψ}}^{″}) + 2 C_{3} (Φ^{'} + {\bar{Φ}}^{'}) + 2 i C_{4} (Φ^{'} - {\bar{Φ}}^{'}) \\ + C_{3} (\bar{w} Φ^{″} + w {\bar{Φ}}^{″}) + i C_{4} (\bar{w} Φ^{″} - w {\bar{Φ}}^{″}) \\ τ_{x y} = h [- i C_{1} (Ψ^{″} - {\bar{Ψ}}^{″}) + C_{2} (Ψ^{″} + {\bar{Ψ}}^{″}) - i C_{3} (\bar{w} Φ^{″} - w {\bar{Φ}}^{″}) + C_{4} (\bar{w} Φ^{″} + w {\bar{Φ}}^{″})] \end{array}}$ (25)

情形2：令 $h^{4} - 2 B_{1} h^{2} + B_{2} = 0$ ， $\frac{\partial^{2} F_{12}}{\partial w \partial \bar{w}} = 0$

假设 $B_{1}^{2} > B_{2}$ ，则得： $h^{2} = B_{1} \pm \sqrt{B_{1}^{2} - B_{2}}$ ，即h有两个根，用 $h_{1}, h_{2}$ 表示，且设 $h_{1} > h_{2}$ 。根据式(13)确定的弹性常数，可将 $h_{1}, h_{2}$ 用工程弹性常数表示为：

$\begin{array}{l} h_{1} = \sqrt{\frac{E_{1}}{2 G_{12}} - μ_{12} + \sqrt{{(\frac{E_{1}}{2 G_{12}} - μ_{12})}^{2} - \frac{E_{1}}{E_{2}}}} \\ h_{1} = \sqrt{\frac{E_{1}}{2 G_{12}} - μ_{12} - \sqrt{{(\frac{E_{1}}{2 G_{12}} - μ_{12})}^{2} - \frac{E_{1}}{E_{2}}}} \end{array}}$ (26)

再由 $\frac{\partial^{2} F_{12}}{\partial w \partial \bar{w}} = 0$ 确定出应力函数 $F_{12}$ 用复变函数表示的一般公式为：

$\begin{matrix} F_{12} = F_{1} (w_{1}, {\bar{w}}_{1}) + F_{2} (w_{2}, {\bar{w}}_{2}) \\ = (C_{1} + i C_{2}) Ψ_{1} + (C_{1} - i C_{2}) \bar{Ψ} {}_{1}+ (C_{3} + i C_{4}) Ψ_{2} + (C_{3} - i C_{4}) {\bar{Ψ}}_{2} \end{matrix}$ (27)

式中复变函数记为： $Ψ_{1} = Ψ_{1} (w_{1})$ ， ${\bar{Ψ}}_{1} = {\bar{Ψ}}_{1} ({\bar{w}}_{1})$ ， $Ψ_{2} = Ψ_{2} (w_{2})$ ， ${\bar{Ψ}}_{2} = {\bar{Ψ}}_{2} ({\bar{w}}_{2})$ 。复变量为： $w_{1} = x + i h_{1} y = r (\cos θ + i h_{1} \sin θ)$ ， $w_{2} = x + i h_{2} y = r (\cos θ + i h_{2} \sin θ)$ 。根据偏导数法则可求出应力函数 $F_{12}$ 的偏导数为：

$\begin{matrix} \frac{\partial^{2} F_{12}}{\partial x^{2}} = (\frac{\partial}{\partial w_{1}} + \frac{\partial}{\partial {\bar{w}}_{1}}) (\frac{\partial F_{1}}{\partial w_{1}} + \frac{\partial F_{1}}{\partial {\bar{w}}_{1}}) + (\frac{\partial}{\partial w_{2}} + \frac{\partial}{\partial {\bar{w}}_{2}}) (\frac{\partial F_{2}}{\partial w_{2}} + \frac{\partial F_{2}}{\partial {\bar{w}}_{2}}) \\ = C_{1} ({Ψ^{″}}_{1} + {\bar{Ψ}}^{″}_{1}) + i C_{2} ({Ψ^{″}}_{1} - {\bar{Ψ}}^{″}_{1}) + C_{3} ({Ψ^{″}}_{2} + {\bar{Ψ}}^{″}_{2}) + i C_{4} ({Ψ^{″}}_{2} - {\bar{Ψ}}^{″}_{2}) \end{matrix}$

$\begin{matrix} \frac{\partial^{2} F_{12}}{\partial x \partial y} = i h_{1} (\frac{\partial}{\partial w_{1}} + \frac{\partial}{\partial {\bar{w}}_{1}}) (\frac{\partial F_{1}}{\partial w_{1}} - \frac{\partial F_{1}}{\partial {\bar{w}}_{1}}) + i h_{2} (\frac{\partial}{\partial w_{2}} + \frac{\partial}{\partial {\bar{w}}_{2}}) (\frac{\partial F_{2}}{\partial w_{2}} - \frac{\partial F_{2}}{\partial {\bar{w}}_{2}}) \\ = i h_{1} C_{1} ({Ψ^{″}}_{1} - {\bar{Ψ}}^{″}_{1}) - h_{1} C_{2} ({Ψ^{″}}_{1} + {\bar{Ψ}}^{″}_{1}) + i h_{2} C_{3} ({Ψ^{″}}_{2} - {\bar{Ψ}}^{″}_{2}) - h_{2} C_{4} ({Ψ^{″}}_{2} + {\bar{Ψ}}^{″}_{2}) \end{matrix}$

$\begin{matrix} \frac{\partial^{2} F_{12}}{\partial y^{2}} = - h_{1}^{2} (\frac{\partial}{\partial w_{1}} - \frac{\partial}{\partial {\bar{w}}_{1}}) (\frac{\partial F_{1}}{\partial w_{1}} - \frac{\partial F_{1}}{\partial {\bar{w}}_{1}}) - h_{2}^{2} (\frac{\partial}{\partial w_{2}} - \frac{\partial}{\partial {\bar{w}}_{2}}) (\frac{\partial F_{2}}{\partial w_{2}} - \frac{\partial F_{2}}{\partial {\bar{w}}_{2}}) \\ = - h_{1}^{2} [C_{1} ({Ψ^{″}}_{1} + {\bar{Ψ}}^{″}_{1}) + i C_{2} ({Ψ^{″}}_{1} - {\bar{Ψ}}^{″}_{1})] - h_{2}^{2} [C_{3} ({Ψ^{″}}_{2} + {\bar{Ψ}}^{″}_{2}) + i C_{4} ({Ψ^{″}}_{2} - {\bar{Ψ}}^{″}_{2})] \end{matrix}$

再按照式(10)确定出应力分量为：

$\begin{array}{l} σ_{x} = - h_{1}^{2} [C_{1} ({Ψ^{″}}_{1} + {\bar{Ψ}}^{″}_{1}) + i C_{2} ({Ψ^{″}}_{1} - {\bar{Ψ}}^{″}_{1})] - h_{2}^{2} [C_{3} ({Ψ^{″}}_{2} + {\bar{Ψ}}^{″}_{2}) + i C_{4} ({Ψ^{″}}_{2} - {\bar{Ψ}}^{″}_{2})] \\ σ_{y} = C_{1} ({Ψ^{″}}_{1} + {\bar{Ψ}}^{″}_{1}) + i C_{2} ({Ψ^{″}}_{1} - {\bar{Ψ}}^{″}_{1}) + C_{3} ({Ψ^{″}}_{2} + {\bar{Ψ}}^{″}_{2}) + i C_{4} ({Ψ^{″}}_{2} - {\bar{Ψ}}^{″}_{2}) \\ τ_{x y} = - i h_{1} C_{1} ({Ψ^{″}}_{1} - {\bar{Ψ}}^{″}_{1}) + h_{1} C_{2} ({Ψ^{″}}_{1} + {\bar{Ψ}}^{″}_{1}) - i h_{2} C_{3} ({Ψ^{″}}_{2} - {\bar{Ψ}}^{″}_{2}) + h_{2} C_{4} ({Ψ^{″}}_{2} + {\bar{Ψ}}^{″}_{2}) \end{array}}$ (28)

以上各公式中的待定常数需要根据边界条件来确定。

4. 裂纹尖端应力场

4.1. 边界条件及坐标变换

断裂力学中最重要的研究目标是确定裂纹端部奇异应力场。对于图1所示的空间裂纹体及图2所选定的坐标系，按极坐标给出上下裂纹面的位置是在 $θ = \pm π$ 处。因此，可将自由裂纹面的应力边界条件表示为：

$σ_{y} = τ_{x y} = τ_{y z} = 0$ $(θ = \pm π)$ (29)

根据裂纹尖端场的相关知识，可将以上公式中的复变函数选定为：

$Ψ^{″} = Φ^{'} = \frac{1}{\sqrt{w}} = \frac{1}{\sqrt{r (\cos θ + i h \sin θ)}}$ (30)

为了使复变函数的实部和虚部容易分解出来，这里采用如下的坐标变换：

$\cos θ = λ^{2} \cos β, h \sin θ = λ^{2} \sin β, h y = h r \sin θ = r λ^{2} \sin β$

则有： $\tan β = h \tan θ$ ， $λ^{4} = \cos^{2} θ + h^{2} \sin^{2} θ$ 。再令 $λ > 0$ ，由此可得：

$β = \arctan (h \tan θ), λ = \sqrt[4]{\cos^{2} θ + h^{2} \sin^{2} θ}$ (31)

显而易见，当 $θ = 0$ 时， $β = 0$ ， $λ = 1$ ；当 $θ = \pm π$ 时， $β = \pm π$ ， $λ = 1$ 。复变量及其复变函数可转化为：

$\begin{array}{l} w = r λ^{2} (\cos β + i \sin β) = r λ^{2} e^{i β} \\ Ψ^{″} = Φ^{'} = \frac{1}{\sqrt{r}} \frac{1}{λ} \exp (- \frac{i β}{2}) = \frac{1}{\sqrt{r}} \frac{1}{λ} (\cos \frac{β}{2} - i \sin \frac{β}{2}) \end{array}}$ (32)

再对 $Φ^{'}$ 求导，并按极坐标可将 $Φ^{″}$ 转化为：

$Φ^{″} = - \frac{1}{2 \sqrt{w^{3}}} = - \frac{1}{2 \sqrt{r}} \frac{1}{r λ^{3}} (\cos \frac{3 β}{2} - i \sin \frac{3 β}{2})$

求出共轭复变函数的和与差，利用三角函数转换关系容易求得：

$Ψ^{″} + {\bar{Ψ}}^{″} = Φ^{'} + {\bar{Φ}}^{'} = \frac{2}{\sqrt{r}} \frac{1}{λ} \cos \frac{β}{2}$

$Ψ^{″} - {\bar{Ψ}}^{″} = Φ^{'} - {\bar{Φ}}^{'} = - i \frac{2}{\sqrt{r}} \frac{1}{λ} \sin \frac{β}{2}$

$\begin{matrix} \bar{w} Φ^{″} + w {\bar{Φ}}^{″} = - \frac{1}{\sqrt{r}} \frac{1}{λ} (\cos β \cos \frac{3 β}{2} - \sin β \sin \frac{3 β}{2}) \\ = - \frac{1}{\sqrt{r}} \frac{1}{λ} (\cos \frac{β}{2} - 2 \sin β \sin \frac{3 β}{2}) \end{matrix}$

$\begin{matrix} \bar{w} Φ^{″} - w {\bar{Φ}}^{″} = i \frac{1}{\sqrt{r}} \frac{1}{λ} (\sin β \cos \frac{3 β}{2} + \cos β \sin \frac{3 β}{2}) \\ = i \frac{1}{\sqrt{r}} \frac{1}{λ} (\sin \frac{β}{2} + 2 \sin β \cos \frac{3 β}{2}) \end{matrix}$

对于不同的参数 $h_{n}$ $(n = 1, 2, 3)$ ，复变量 $w_{n}$ 可表达为：

$w_{n} = r λ_{n}^{2} (\cos β_{n} + i \sin β_{n}) = r λ_{n}^{2} \exp (i β_{n})$ (33)

且有： $β_{n} = \arctan (h_{n} \tan θ)$ ， $λ_{n} = \sqrt[4]{\cos^{2} θ + h_{n}^{2} \sin^{2} θ}$ 。

4.2. 应力分量与应力强度因子

利用以上选定的复变函数及转换关系式，可确定出应力分量的具体函数表达式。两个切应力表达式(22)可转变为：

$\begin{array}{l} τ_{y z} = 2 A_{3} Re \frac{1}{\sqrt{r}} \frac{1}{λ_{3}} (\cos \frac{β_{3}}{2} - i \sin \frac{β_{3}}{2}) = \frac{2 A_{3}}{\sqrt{r}} \frac{1}{λ_{3}} \cos \frac{β_{3}}{2} \\ τ_{x z} = 2 A_{3} h_{3} Im \frac{1}{\sqrt{r}} \frac{1}{λ_{3}} (\cos \frac{β_{3}}{2} - i \sin \frac{β_{3}}{2}) = - 2 A_{3} h_{3} \frac{1}{\sqrt{r}} \frac{1}{λ_{3}} \sin \frac{β_{3}}{2} \end{array}}$ (34)

对于裂纹面， $β_{3} = \pm π$ ， $τ_{y z} = 0$ ，应力边界条件自动满足。在裂纹前沿 $(θ = 0)$ 应力具有奇异性，应力强度因子 $K_{I I I}$ 按如下确定 $(β_{3} = 0, λ_{3} = 1)$ ：

$K_{I I I} = \lim_{r \to 0} \sqrt{2 π r} {τ_{y z} |}_{θ = 0} = 2 A_{3} \sqrt{2 π}$

从而常数 $A_{3}$ 可以确定： $2 A_{3} = \frac{K_{I I I}}{\sqrt{2 π}}$ 。因此，应力分量既可表示为：

$\begin{array}{l} τ_{y z} = \frac{K_{I I I}}{\sqrt{2 π r}} \frac{1}{λ_{3}} \cos \frac{β_{3}}{2} \\ τ_{x z} = - \frac{K_{I I I}}{\sqrt{2 π r}} \frac{h_{3}}{λ_{3}} \sin \frac{β_{3}}{2} \end{array}}$ (35)

接下来继续确定另外的应力分量。对于情形1，为了化简应力分量公式(25)，先利用式(32)及各个共轭函数关系式将应力表达式(25)转化为：

$\begin{array}{l} σ_{x} = - (C_{1} - 2 C_{3}) \frac{2}{\sqrt{r}} \frac{h^{2}}{λ} \cos \frac{β}{2} - (C_{2} - 2 C_{4}) \frac{2}{\sqrt{r}} \frac{h^{2}}{λ} \sin \frac{β}{2} \\ + \frac{C_{3}}{\sqrt{r}} \frac{h^{2}}{λ} (\cos \frac{β}{2} - 2 \sin β \sin \frac{3 β}{2}) + \frac{C_{4}}{\sqrt{r}} \frac{h^{2}}{λ} (\sin \frac{β}{2} + 2 \sin β \cos \frac{3 β}{2}) \\ σ_{y} = (C_{1} + 2 C_{3}) \frac{2}{\sqrt{r}} \frac{1}{λ} \cos \frac{β}{2} + (C_{2} + 2 C_{4}) \frac{2}{\sqrt{r}} \frac{1}{λ} \sin \frac{β}{2} \\ - \frac{C_{3}}{\sqrt{r}} \frac{1}{λ} (\cos \frac{β}{2} - 2 \sin β \sin \frac{3 β}{2}) - \frac{C_{4}}{\sqrt{r}} \frac{1}{λ} (\sin \frac{β}{2} + 2 \sin β \cos \frac{3 β}{2}) \\ τ_{x y} = - \frac{2 C_{1}}{\sqrt{r}} \frac{h}{λ} \sin \frac{β}{2} + \frac{2 C_{2}}{\sqrt{r}} \frac{h}{λ} \cos \frac{β}{2} \frac{C_{3}}{\sqrt{r}} \frac{h}{λ} (\sin \frac{β}{2} + 2 \sin β \cos \frac{3 β}{2}) \\ - \frac{C_{4}}{\sqrt{r}} \frac{h}{λ} (\cos \frac{β}{2} - 2 \sin β \sin \frac{3 β}{2}) \end{array}}$ (36)

对于裂纹面 $(θ = \pm π)$ ，应力边界条件为 $β = \pm π$ ， $σ_{y} = τ_{x y} = 0$ ，由此可求得：

$2 C_{2} = - 3 C_{4}, C_{3} = 2 C_{1}$

在裂纹前沿 $(θ = 0)$ 应力具有奇异性，可由正应力 $σ_{y}$ 和切应力 $τ_{x y}$ 分别确定出应力强度因子 $K_{I}$ 和 $K_{I I}$ 。按如下方法确定 $(β = 0, λ = 1)$ ：

$K_{I} = \lim_{r \to 0} \sqrt{2 π r} {σ_{y} |}_{θ = 0} = 8 C_{1} \sqrt{2 π}, K_{I I} = \lim_{r \to 0} \sqrt{2 π r} {τ_{x y} |}_{θ = 0} = - 4 C_{4} h \sqrt{2 π}$

可得： $8 C_{1} = 4 C_{3} = \frac{K_{I}}{\sqrt{2 π}}$ ， $- 4 C_{4} h = \frac{8 C_{2} h}{3} = \frac{K_{I I}}{\sqrt{2 π}}$

将确定的常数代入应力分量表达式(36)，化简后的裂纹尖端应力公式为：

$\begin{array}{l} σ_{x} = \frac{K_{I}}{\sqrt{2 π r}} \frac{h^{2}}{λ} \cos \frac{β}{2} (1 - \sin \frac{β}{2} \sin \frac{3 β}{2}) - \frac{K_{I I}}{\sqrt{2 π r}} \frac{h}{λ} \sin \frac{β}{2} (2 + \cos \frac{β}{2} \cos \frac{3 β}{2}) \\ σ_{y} = \frac{K_{I}}{\sqrt{2 π r}} \frac{1}{λ} \cos \frac{β}{2} (1 + \sin \frac{β}{2} \sin \frac{3 β}{2}) + \frac{K_{I I}}{\sqrt{2 π r}} \frac{1}{h λ} \sin \frac{β}{2} \cos \frac{β}{2} \cos \frac{3 β}{2} \\ τ_{x y} = \frac{K_{I}}{\sqrt{2 π r}} \frac{h}{λ} \sin \frac{β}{2} \cos \frac{β}{2} \cos \frac{3 β}{2} + \frac{K_{I I}}{\sqrt{2 π r}} \frac{1}{λ} \cos \frac{β}{2} (1 - \sin \frac{β}{2} \sin \frac{3 β}{2}) \end{array}}$ (37)

对于情形2，为了化简应力分量公式(28)，先利用式(32)及各个共轭函数关系式将应力表达式(28)转化为：

$\begin{array}{l} σ_{x} = - \frac{2}{\sqrt{r}} [h_{1}^{2} (\frac{C_{1}}{λ_{1}} \cos \frac{β_{1}}{2} + \frac{C_{2}}{λ_{1}} \sin \frac{β_{1}}{2}) + h_{2}^{2} (\frac{C_{3}}{λ_{2}} \cos \frac{β_{2}}{2} + \frac{C_{4}}{λ_{2}} \sin \frac{β_{2}}{2})] \\ σ_{y} = \frac{2}{\sqrt{r}} (\frac{C_{1}}{λ_{1}} \cos \frac{β_{1}}{2} + \frac{C_{2}}{λ_{1}} \sin \frac{β_{1}}{2} + \frac{C_{3}}{λ_{2}} \cos \frac{β_{2}}{2} + \frac{C_{4}}{λ_{2}} \sin \frac{β_{2}}{2}) \\ τ_{x y} = \frac{2}{\sqrt{r}} (- \frac{h_{1} C_{1}}{λ_{1}} \sin \frac{β_{1}}{2} + \frac{h_{1} C_{2}}{λ_{1}} \cos \frac{β_{1}}{2} - \frac{h_{2} C_{3}}{λ_{2}} \sin \frac{β_{2}}{2} + \frac{h_{2} C_{4}}{λ_{2}} \cos \frac{β_{2}}{2}) \end{array}}$ (38)

对于裂纹面 $(θ = \pm π, λ_{1} = λ_{2} = 1)$ ，应力边界条件为 $σ_{y} = τ_{x y} = 0$ ， $(β_{1} = β_{2} = \pm π)$ ，由此可得出常数关系为：

$C_{2} + C_{4} = 0, h_{1} C_{1} + h_{2} C_{3} = 0$

在裂纹前沿 $(θ = 0)$ 应力具有奇异性，可由正应力 $σ_{y}$ 和切应力 $τ_{x y}$ 分别确定出应力强度因子 $K_{I}$ 和 $K_{I I}$ 。按如下方法确定 $(β_{1} = β_{2} = 0, λ_{1} = λ_{2} = 1)$ ：

$K_{I} = \lim_{r \to 0} \sqrt{2 π r} {σ_{y} |}_{θ = 0} = 2 (C_{1} + C_{3}) \sqrt{2 π} = 2 C_{3} (1 - \frac{h_{2}}{h_{1}}) \sqrt{2 π}$

$K_{I I} = \lim_{r \to 0} \sqrt{2 π r} {τ_{x y} |}_{θ = 0} = 2 (h_{1} C_{2} + h_{2} C_{4}) \sqrt{2 π} = 2 C_{2} (h_{1} - h_{2}) \sqrt{2 π}$

可得： $2 C_{3} h_{2} = - 2 C_{1} h_{1} = \frac{K_{I}}{\sqrt{2 π}} \frac{h_{1} h_{2}}{h_{1} - h_{2}}$ ， $2 C_{2} = - 2 C_{4} = \frac{K_{I I}}{\sqrt{2 π}} \frac{1}{h_{1} - h_{2}}$

将确定的常数代入应力分量表达式(38)，化简后的裂纹端部应力公式为：

$\begin{array}{l} σ_{x} = \frac{K_{I}}{\sqrt{2 π r}} \frac{h_{1} h_{2}}{h_{1} - h_{2}} (\frac{h_{1}}{λ_{1}} \cos \frac{β_{1}}{2} - \frac{h_{2}}{λ_{2}} \cos \frac{β_{2}}{2}) - \frac{K_{I I}}{\sqrt{2 π r}} \frac{1}{h_{1} - h_{2}} (\frac{h_{1}^{2}}{λ_{1}} \sin \frac{β_{1}}{2} - \frac{h_{2}^{2}}{λ_{2}} \sin \frac{β_{2}}{2}) \\ σ_{y} = \frac{K_{I}}{\sqrt{2 π r}} \frac{1}{h_{1} - h_{2}} (\frac{h_{1}}{λ_{2}} \cos \frac{β_{2}}{2} - \frac{h_{2}}{λ_{1}} \cos \frac{β_{1}}{2}) + \frac{K_{I I}}{\sqrt{2 π r}} \frac{1}{h_{1} - h_{2}} (\frac{1}{λ_{1}} \sin \frac{β_{1}}{2} - \frac{1}{λ_{2}} \sin \frac{β_{2}}{2}) \\ τ_{x y} = \frac{K_{I}}{\sqrt{2 π r}} \frac{h_{1} h_{2}}{h_{1} - h_{2}} (\frac{1}{λ_{1}} \sin \frac{β_{1}}{2} - \frac{1}{λ_{2}} \sin \frac{β_{2}}{2}) + \frac{K_{I I}}{\sqrt{2 π r}} \frac{1}{h_{1} - h_{2}} (\frac{h_{1}}{λ_{1}} \cos \frac{β_{1}}{2} - \frac{h_{2}}{λ_{2}} \cos \frac{β_{2}}{2}) \end{array}}$ (39)

这里还要说明，以上应力公式中没有采用实际角度 $θ$ ，而是用变换的角度 $β$ 才使得公式简明。应力表达式中包含材料参数( $h, λ$ )，这与各向同性材料形成明显差异，也显示出各向异性材料的复杂性。各向同性材料的应力场取决于几何尺寸和边界条件，与材料特性无关，而各向异性材料应力分布与材料性能密切相关。还要指出，文中忽略了z方向的正应力，但对于厚板就不合理了，设定 $σ_{z} \approx 0$ 只是为了简化分析。在理论分析时取自由裂纹表面为±180˚，这是理想情况，在实际问题中两个裂纹面之间可能有一定间隔，但对于裂纹尖端应力影响很小，应力公式仍然适用。

5. 结论

采用线弹性力学方法分析I + II + III混合型裂纹尖端应力场，得到了正交异性材料混合型裂纹尖端区的应力通解(忽略 $σ_{z}$ )。综上所述，正交异性材料裂纹尖端区的混合型应力场可按两种情况表达如下：

① 特定情况 ${(\frac{E_{1}}{2 G_{12}} - μ_{12})}^{2} = \frac{E_{1}}{E_{2}}$

② 通常情况 ${(\frac{E_{1}}{2 G_{12}} - μ_{12})}^{2} > \frac{E_{1}}{E_{2}}$

基金项目

国家自然科学基金资助(No: 51475372)。

文章引用

贾普荣. 正交异性材料I + II + III混合型裂纹尖端应力分析
Crack-Tip Stress Analysis for Orthotropic Materials under Mixed-Mode I + II + III Loading[J]. 力学研究, 2020, 09(04): 123-134. https://doi.org/10.12677/IJM.2020.94014

参考文献

1. 李群, 欧卓成, 陈宜亨. 高等断裂力学[M]. 北京: 科学出版社, 2017.

2. 郦正能, 张纪奎. 工程断裂力学[M]. 北京: 北京航空航天大学出版社，2012.

3. Sih, G.C. (1991) Mechanics of Fracture Initiation and Propagation. Kluwer Academic Publishers, Netherlands.

4. 张行. 断裂与损伤力学[M]. 北京: 北京航空航天大学出版社, 2009.

5. 杨维阳, 李俊林, 张雪霞. 复合材料断裂复变方法[M]. 北京: 科学出版社, 2005.

6. Zhang, H. and Qiao, P. (2019) A State-Based Peridynamic Model for Quantitative Elastic and Fracture Analysis of Orthotropic Mate-rials. Engineering Fracture Mechanics, 206, 147-171.

7. Jia, P., Suo, Y., Jia, C. and Wang, Q. (2019) Stress Analysis of Orthotropic Wedge Loaded on the Apex. IOP Conference Series: Materials Science and Engineering, 5th Annual International Workshop on Materials Science and Engineering, Vol. 585, Changsha, 17-18 May 2019, 448-453.

8. 贾普荣, 锁永永. 正交异性材料平面裂纹尖端应力场[J]. 应用力学学报, 2020, 37(1): 78-85.

9. 贾普荣. 正交异性板裂纹端部应力及变形通解[J]. 力学研究, 2020, 9(2): 70-76.

期刊菜单