Software Engineering and Applications
Vol.06 No.04(2017), Article ID:21608,9
pages
10.12677/SEA.2017.64007
Study on Trajectory Tracking Control of Two-Wheel Difference Speed of AGV
Lipeng Yang, Wenfeng Zhang, Hao Wang
Shanghai University of Electric Power, College Of Energy and Mechanical Engineering, Shanghai

Received: Jul. 18th, 2017; accepted: Aug. 1st, 2017; published: Aug. 7th 2017

ABSTRACT
In view of trajectory tracking control problem of AGV, a Back-stepping control algorithm is proposed. Firstly, the AGV kinematics model and tracking pose error model are established; Then, the whole nonlinear system is decomposed into several sub-systems by using Back-stepping method, and the Lyapunov function and the intermediate virtual control are constructed and has been back to export control law of system step by step. Finally, the simulation experiment of line tracking and circular tracking was carried out in MATLAB environment. The results show that the tracking error converges to zero quickly, and trajectory tracking effect is wonderful. Back-stepping method combined with Lyapunov theory design the controller, not only can achieve AGV on the reference trajectory global asymptotic tracking, but also has high accuracy and robustness.
Keywords:AGV, Back-Stepping, Trajectory Tracking, Lyapunov
两轮差速AGV的轨迹跟踪控制研究
杨李朋,张文丰,王昊
上海电力学院 能源与机械工程学院,上海
收稿日期:2017年7月18日;录用日期:2017年8月1日;发布日期:2017年8月7日

摘 要
本文针对AGV的轨迹跟踪控制问题,提出了一种Back-stepping的控制算法。首先,建立AGV的运动学模型和跟踪位姿误差模型;然后,利用Back-stepping方法将整个非线性系统进行分解成若干子系统,且对子系统分步构造Lyapunov函数和中间虚拟控制量,一直后退导出系统的控制律;最后,在MATLAB环境下分别进行了直线轨迹跟踪和圆轨迹跟踪的仿真实验,结果表明跟踪误差很快收敛于零,轨迹跟踪效果良好。Back-stepping方法结合Lyapunov理论设计的控制器,不仅能实现对AGV对参考轨迹全局渐进跟踪,还具有较高的精确性和鲁棒性。
关键词 :AGV,Back-stepping,轨迹跟踪,Lyapunov

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自动引导小车(Automatic Guided Vehicles, AGV)能够承重一定载荷且沿着给定路径精确地自动行驶 [1] 。利用传感器能够探索周围环境并自动完成寻找最优路径和自身的定位及跟踪设定的轨迹,在进行高层次的决策程序时,底层基本的轨迹跟踪需要进行严格的控制 [2] 。AGV系统是一个强耦合的非线性动力学系统,存在着各种参数和非参数的不确定性,且具有车轮摩擦、负载的变化和噪声等外界的不确定因素。传统的基于对象的控制方法很难精确地进行轨迹跟踪。近年来,AGV的智能控制在理论和应用方面都取得较大的进展。AGV的运动控制方法主要有模糊控制 [3] ,模型预测控制 [4] ,自适应控制 [5] ,神经网络控制 [6] 等。这些智能控制方法均对非线性系统有着较好的自适应性,但是仅限于局部渐进稳定,且控制器设计比较复杂。
本文首先建立了AGV的运动学模型,在该模型的基础上采用Back-stepping算法和Lyapunov理论设计控制器,确保AGV系统对参考轨迹的全局渐进跟踪。通过MATLAB仿真实验,验证了AGV轨迹跟踪的有效性。
2. AGV的运动学模型
AGV是通过左右两个驱动轮之间的速度差来改变小车的运动方向,属于两自由度的驱动系统。因为驱动轮和地面的滚动约束比较复杂,针对小车的实际运行情况建立精确的运动学模型是比较困难的。为了进行运动学建模,将问题做如下假设和简化:假设车轮在路面上低速运行,忽略车轮滑动的影响,并且两驱动轮保持在同一轴线上 [7] 。
两轮差动驱动的AGV模型如图1所示。取左右两轮中心连线的中点C作为参考点,则小车的位姿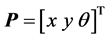 ,设
,设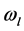 和
和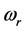 分别为左、右驱动轮的角速度,
分别为左、右驱动轮的角速度,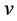 和
和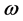 分别是小车的线速度和转动角速度,则运动学模型 [8] [9] 为
分别是小车的线速度和转动角速度,则运动学模型 [8] [9] 为
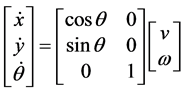 (1)
(1)
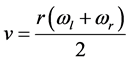 (2)
(2)
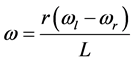 (3)
(3)
其中,θ为AGV的航向角,L为左、右两轮的长度,r为车轮的半径。
AGV位姿误差模型如图2所示,小车的实际位姿为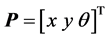 ,参考位姿为
,参考位姿为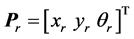 ,位姿
,位姿
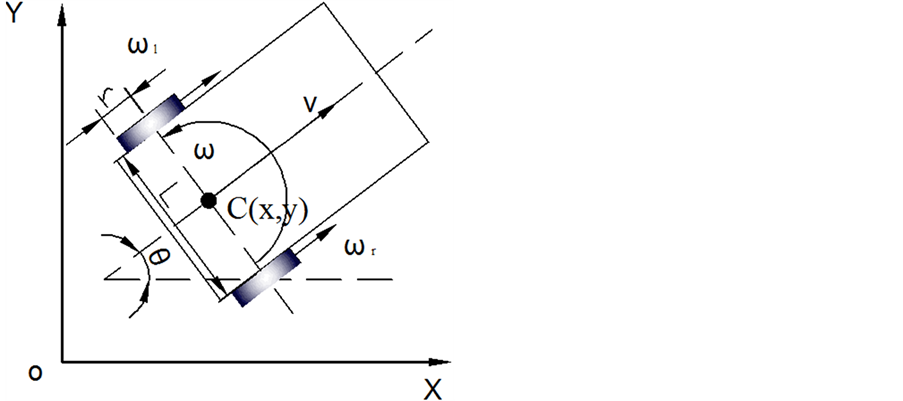
Figure 1. Two-wheel differential drive AGV model
图1. 两轮差速驱动AGV模型

Figure 2. AGV pose error model
图2. AGV位姿误差模型
误差则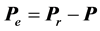 ,以
,以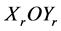 为参考坐标系,根据坐标变换公式得到AGV位姿误差为 [10] [11] [12] :
为参考坐标系,根据坐标变换公式得到AGV位姿误差为 [10] [11] [12] :
 (4)
(4)
对式(4)进行时间求导得出以下方程:
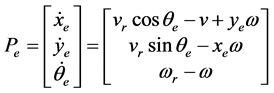 (5)
(5)
由以上分析可以看出,AGV的轨迹跟踪问题可以转化为设计一个有界控制输入量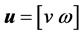 ,在任意初始的误差下,可以使AGV的实际位姿能够快速地跟踪参考位姿 [13] [14] 。即:取下面的闭环反馈非线性系统 [15] :
,在任意初始的误差下,可以使AGV的实际位姿能够快速地跟踪参考位姿 [13] [14] 。即:取下面的闭环反馈非线性系统 [15] :
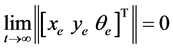 (6)
(6)
3. Back-stepping 控制律的设计
3.1. Back-stepping设计步骤
取下面的闭环反馈非线性系统
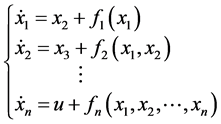 (7)
(7)
其中,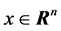 是系统的状态,
是系统的状态,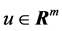 是系统的输入,
是系统的输入,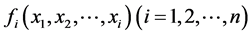 是系统的非线性部分。
是系统的非线性部分。
Back-stepping方法的设计思想是把每一个子系统 中的
中的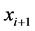 作为虚拟控制量,通过适当的
作为虚拟控制量,通过适当的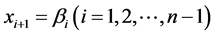 来满足前面的系统状态的渐进稳定,因为
来满足前面的系统状态的渐进稳定,因为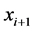 不是实际的控制量,所以引进误差变量
不是实际的控制量,所以引进误差变量 ,通过设定虚拟反馈控制变量
,通过设定虚拟反馈控制变量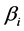 与
与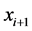 具有线性特性,使整个系统达到渐进稳定。
具有线性特性,使整个系统达到渐进稳定。
引入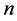 个虚拟反馈变量误差,把式(7)第一个等式作为一个独立的子系统。
个虚拟反馈变量误差,把式(7)第一个等式作为一个独立的子系统。
 (8)
(8)
为保证系统的每个状态都趋于渐进稳定,要在每个状态都构造一个Lyapunov函数。下面对每个系统的状态进行设计。
第一步:对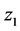 进行求导得:
进行求导得:
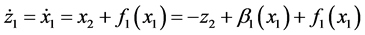 (9)
(9)
取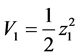 ,令
,令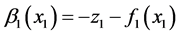 。
。
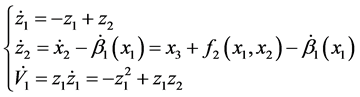 (10)
(10)
若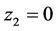 ,
,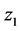 渐进稳定,若
渐进稳定,若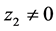 ,需要再次引入虚拟反馈变量
,需要再次引入虚拟反馈变量 使误差变量
使误差变量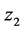 具有渐进稳定性。
具有渐进稳定性。
第二步:定义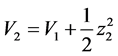 ,令
,令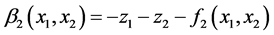
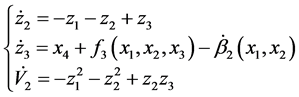 (11)
(11)
若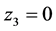 ,则
,则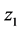 和
和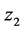 渐进稳定;若
渐进稳定;若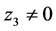 ,需要引入虚拟反馈变量
,需要引入虚拟反馈变量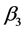 使误差变量
使误差变量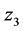 具有渐近稳定性。按照这种方法递推下去,找到一般的虚拟反馈变量和Lyapunov函数。
具有渐近稳定性。按照这种方法递推下去,找到一般的虚拟反馈变量和Lyapunov函数。
第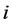 步:定义一般的虚拟反馈变量和Lyapunov函数如下。
步:定义一般的虚拟反馈变量和Lyapunov函数如下。
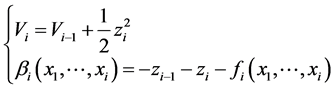 (12)
(12)
则有
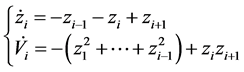 (13)
(13)
由此递推到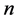 步得
步得
 (14)
(14)
则系统的最终的控制律为
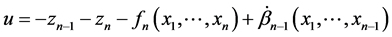 (15)
(15)
综上可知,误差变量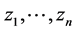 以指数形式渐进稳定,即整个系统是趋于渐进稳定的。
以指数形式渐进稳定,即整个系统是趋于渐进稳定的。
3.2. 控制器的设计
当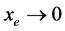 且
且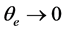 ,则
,则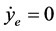 ,即
,即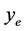 趋于常数,不能对系统进行控制。假设
趋于常数,不能对系统进行控制。假设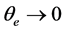 ,
, 为虚拟控制输入,然后找到合适虚拟反馈状态使
为虚拟控制输入,然后找到合适虚拟反馈状态使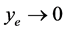 。
。
由AGV位姿误差微分方程(5)可知,当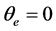 时,选取控制Lyapunov函数为:
时,选取控制Lyapunov函数为:
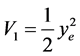 (16)
(16)
对(16)微分得:
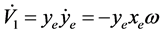 (17)
(17)
设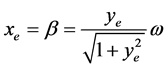 ,则
,则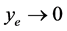 。AGV的轨迹跟踪控制律的设计输入为
。AGV的轨迹跟踪控制律的设计输入为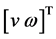 ,取误差变量为:
,取误差变量为:
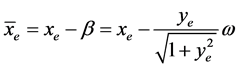 (18)
(18)
在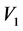 的基础上构造Lyapunov函数为:
的基础上构造Lyapunov函数为:
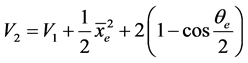 (19)
(19)
对式(19)微分得:
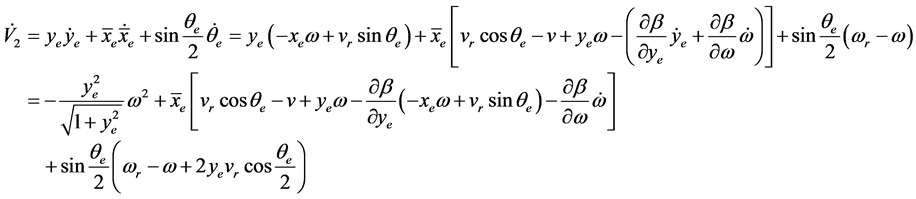 (20)
(20)
设计的控制律如下:
 (21)
(21)
其中: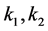 是正常数。将设计控制律代入式(20)得:
是正常数。将设计控制律代入式(20)得:
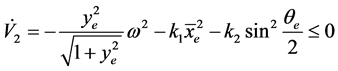 (22)
(22)
因此,采用式(22)所示的反馈控制律能够使控制系统渐进收敛于稳定平衡点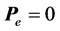
为了减小系统的抖振问题,采用了滑模变结构的控制方法,引进了等速趋近律 [16] 。
令
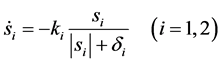 (23)
(23)
其中,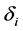 为正小数,
为正小数,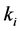 为正常数。
为正常数。
由上述表达式设计切换函数如下:
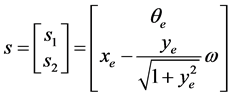 (24)
(24)
由式(23)和式(24)得
 (25)
(25)
整理得,设计的控制律如下:
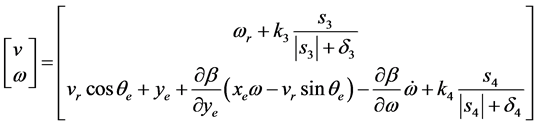 (26)
(26)
4. 仿真验证
在MATLAB环境下对Back-stepping控制算法的控制性能进行验证。对AGV分别进行了直线轨迹跟踪控制和圆轨迹跟踪控制。AGV控制律参数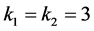 ,初始速度均为
,初始速度均为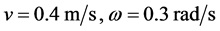 。
。
1) 当AGV按照直线路径进行跟踪时:初始位姿误差为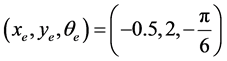 ,期望速度为
,期望速度为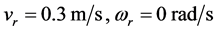 ,仿真结果如图3所示。
,仿真结果如图3所示。
2) 当AGV按照圆路径进行跟踪时:初始位姿误差为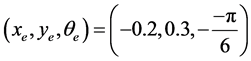 ,期望速度为
,期望速度为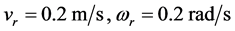 ,仿真结果如下图3~图8所示。
,仿真结果如下图3~图8所示。
从图4和图6可以看出AGV都能够快速、准确地按照规定的线路行驶,从图3和图5可以看出AGV能快速到达期望的速度。说明所设计控制律具有很好的轨迹跟踪能力,表现为跟踪路径精确程度高,跟踪速度快,稳定性好,验证了Back-stepping控制方法的有效性和正确性。
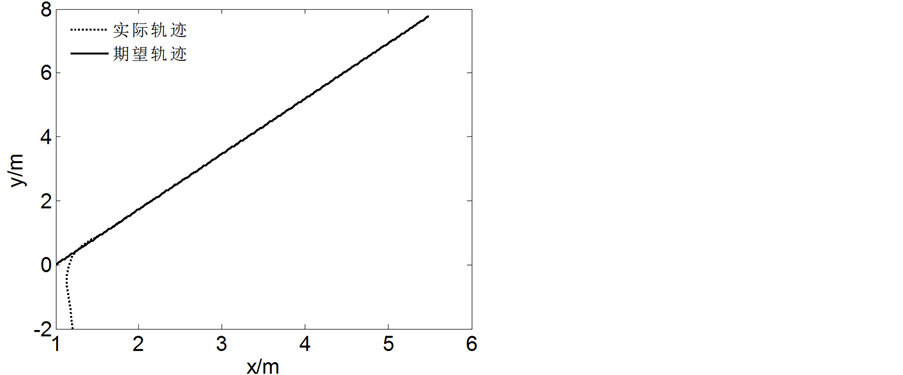
Figure 3. Tracking error of linear trajectory
图3. 直线轨迹的跟踪误差
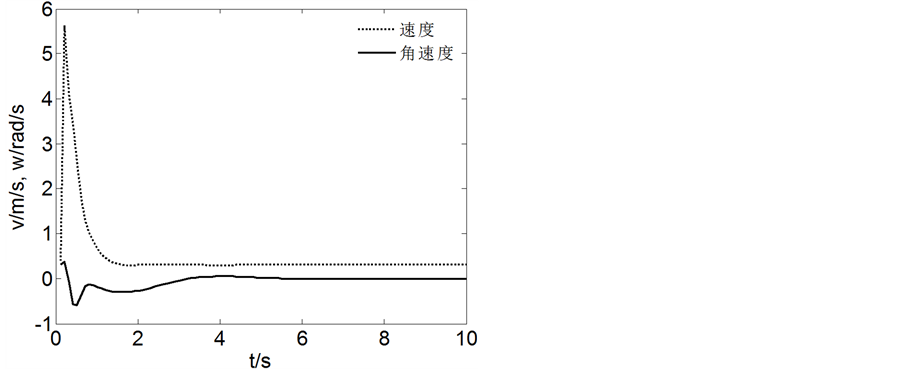
Figure 4. Linear trajectory tracking speed changes
图4. 直线轨迹跟踪速度变化
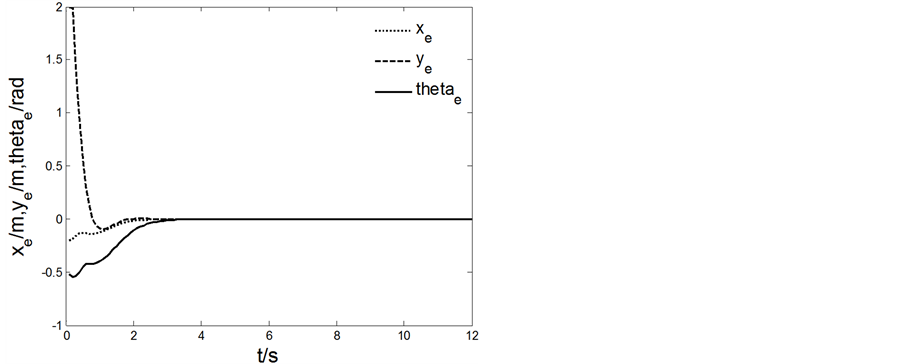
Figure 5. Linear trajectory tracking pose error curve
图5. 直线轨迹跟踪位姿误差曲线

Figure 6. Tracking error of circular trajectory
图6. 圆轨迹的跟踪误差
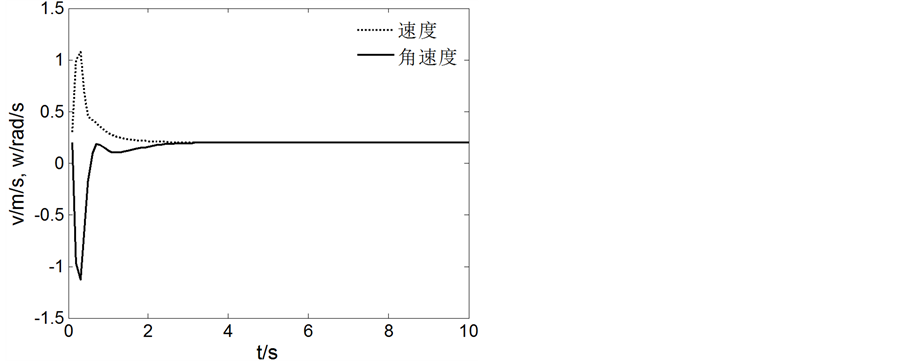
Figure 7. Linear trajectory tracking speed changes
图7. 直线轨迹跟踪速度变化
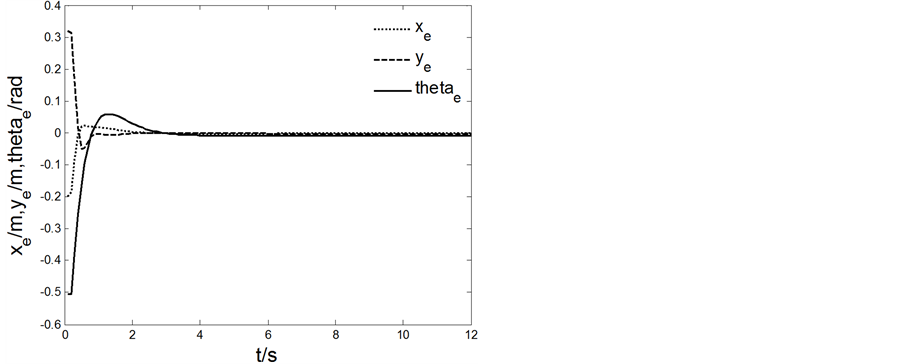
Figure 8. Round track tracking pose error curve
图8. 圆轨迹跟踪位姿误差曲线
5. 结论
本文采用Back-stepping的方法来对AGV进行轨迹跟踪控制,建立了AGV运动学模型,运用了反演法且结合Lyapunov理论间接的设计了轨迹跟踪控制律,使小车趋向于全局稳定。仿真结果表明AGV能够实时、快速地跟踪参考轨迹,具有良好的控制效果,验证了Back-stepping控制方法的有效性。
文章引用
杨李朋,张文丰,王 昊. 两轮差速AGV的轨迹跟踪控制研究
Study on Trajectory Tracking Control of Two-Wheel Difference Speed of AGV[J]. 软件工程与应用, 2017, 06(04): 59-67. http://dx.doi.org/10.12677/SEA.2017.64007
参考文献 (References)
- 1. Pratama, P.S. and Gulakari, A.V. (2016) Trajectory Tracking and Fault Detection Algorithm for Automatic Guided Vehicle Based on Multiple Positioning Modules. International Journal of Control, Automation and Systems, 14, 400- 410. https://doi.org/10.1007/s12555-014-0294-y
- 2. Pratama, P.S., Luan, B.T., et al. (2014) Trajectory Tracking Algorithm for Automatic Guided Vehicle Based on Adaptive Backstepping Control Method. Recent Advances in Electrical Engineering and Related Sciences, 11, 535-543. https://doi.org/10.1007/978-3-642-41968-3_53
- 3. 王海燕. 基于全局PID模糊滑模算法的机器人跟踪控制仿真[J]. 西南师范大学学报, 2015, 40(10): 57-63.
- 4. Zhu, M. and Chen, H.Y. (2016) A Model Predictive Speed Tracking Control Approach for Autonomous Ground Vehicles. Mechanical Systems and Signal Processing, 12, 68-75.
- 5. 康浩博, 王建辉. 基于安全性考虑的五自由度外骨骼式上肢康复机器人自适应控制[J]. 中国科技论文, 2014, 9(7): 844-851.
- 6. Xin, L.J. and Wang, Q.L. (2016) Robust Adaptive Tracking Control of Wheeled Mobile Robot. Robotics and Autonomous Systems, 78, 36-48. https://doi.org/10.1016/j.robot.2016.01.002
- 7. 卢彬. 基于单片机的差速驱动导引小车运动控制[D]: [硕士学位论文]. 西安: 西安理工大学, 2010.
- 8. Huang, H.-C. and Chiang, C.-H. (2016) An Evolutionary Radial Basis Function Neural Network with Robust Genetic-Based Immunecomputing for Online Tracking Control of Autonomous Robots. Neural Processing Letters, 44, 19- 35. https://doi.org/10.1007/s11063-015-9452-3
- 9. Yin, X.-H. and Zhao, H. (2013) On a New Sectionalized Motion Control Strategy for Automated Guided Vehicles: Modeling and Simulation Validation. Robotics, 69, 637-646. https://doi.org/10.1007/s00170-013-5035-5
- 10. 王仲民, 岳宏, 刘继岩. 轮式移动机器人轨迹跟踪控制[J]. 太原理工大学学报, 2005, 4(36): 474-476.
- 11. Pratama, P.S., Jeong, J.H., et al. (2016) Adaptive Backstepping Control Design for Trajectory Tracking of Automatic Guided Vehicles. Lecture Notes in Electrical Engineering, 9, 589-602. https://doi.org/10.1007/978-3-319-27247-4_50
- 12. 吕学勤, 陈文君, 吴毅雄. 基于Back-Stepping 的机器人轨迹跟踪[J]. 机器人与自动化, 2013, 24(9): 56-61.
- 13. Klančar, G., Matko, D. and Blažič, S. (2011) A Control Strategy for Platoons of Differential Drive Wheeled Mobile Robot. Robotics and Autonomous Systems, 59, 57-64. https://doi.org/10.1016/j.robot.2010.12.002
- 14. 吴剑, 黄晓娟, 江维. 基于Back-stepping 的轮式机器人轨迹跟踪[J]. 南昌航空大学学报, 2012, 4(26): 89-93.
- 15. 李平, 王建锋, 李娜, 惠珂. 基于lyapunov直接法的移动机器人运动控制研究[J]. 中国科技论文, 2016, 2(11): 160-163.
- 16. 叶锦华, 李迪, 叶峰. 不确定完整AGV的自适应反演滑模控制[J]. 华南理工大学学报, 2011, 39(12): 32-37.