Astronomy and Astrophysics
Vol.05 No.02(2017), Article ID:20293,6
pages
10.12677/AAS.2017.52003
Problems and Thoughts on the State Equation of Ideal Gas
Xinglai Shao, Wei Wang, Yaoming Zhou
The National 305 Project Office of Xinjiang Uygur Autonomous Region, Urumqi Xinjiang

Received: Apr. 11th, 2017; accepted: Apr. 25th, 2017; published: Apr. 28th, 2017

ABSTRACT
The ideal gas equation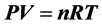 has already become the basic knowledge of physics curriculum and the physical formula that must be observed, but the volume of gas in the free space of the atmosphere is not fixed. The air density at the formula
has already become the basic knowledge of physics curriculum and the physical formula that must be observed, but the volume of gas in the free space of the atmosphere is not fixed. The air density at the formula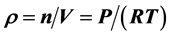 is directly proportional to the pressure, which will conflict with some phenomena. This paper uses altitude H instead of pressure P to obtain free space air density
is directly proportional to the pressure, which will conflict with some phenomena. This paper uses altitude H instead of pressure P to obtain free space air density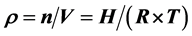 to indicate that the air density with altitude increases exponentially, and leads a negative correlation with temperature. At the same time, the air of the free space should gather from the high pressure place to the place where the pressure is low. It means that the higher the altitude, the lower the pressure, and the air density will increase. The air density calculation formula is deduced from the gaseous equation, and it Calculates a result that troposphere air density at 12 kilometers has increased 15 times than the standard atmospheric pressure P0, and the exosphere at 1000 kilometers has increased 187 fold. Of course, this conclusion is totally opposite with the basic knowledge of “the higher the altitude, the thinner the air”. The reason is perhaps that we neglect the matter named H which has natural content of 99.985%. From this, we can have a corollary that any matter in atmospheric space may be divided into the most simple-matter-H (proton). It will become “neutron” when losing the orbital electrons at the ionized layer, and then it will “escape” into the universe to constitute new materials and planets in a new way and new form. This may be a way by which the earth's materials exchange with the planet’s materials through the atmosphere.
to indicate that the air density with altitude increases exponentially, and leads a negative correlation with temperature. At the same time, the air of the free space should gather from the high pressure place to the place where the pressure is low. It means that the higher the altitude, the lower the pressure, and the air density will increase. The air density calculation formula is deduced from the gaseous equation, and it Calculates a result that troposphere air density at 12 kilometers has increased 15 times than the standard atmospheric pressure P0, and the exosphere at 1000 kilometers has increased 187 fold. Of course, this conclusion is totally opposite with the basic knowledge of “the higher the altitude, the thinner the air”. The reason is perhaps that we neglect the matter named H which has natural content of 99.985%. From this, we can have a corollary that any matter in atmospheric space may be divided into the most simple-matter-H (proton). It will become “neutron” when losing the orbital electrons at the ionized layer, and then it will “escape” into the universe to constitute new materials and planets in a new way and new form. This may be a way by which the earth's materials exchange with the planet’s materials through the atmosphere.
Keywords:Gas Equation, Free Space, Gas Density, Planet Matter

理想气体状态方程的问题和思考
邵行来,王威,周耀明
新疆维吾尔自治区人民政府国家三〇五项目办公室,新疆 乌鲁木齐
收稿日期:2017年4月11日;录用日期:2017年4月25日;发布日期:2017年4月28日

摘 要
理想气体气态方程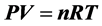 早已成了物理课程的基本常识和必须遵守的物理公式,但在大气的自由空间里气体体积是不能固定的。这时的空气密度
早已成了物理课程的基本常识和必须遵守的物理公式,但在大气的自由空间里气体体积是不能固定的。这时的空气密度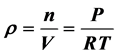 ,与压强成正比,这就会与一些现象发生矛盾。本文用海拔高度H代替压力P得出了自由空间空气密度
,与压强成正比,这就会与一些现象发生矛盾。本文用海拔高度H代替压力P得出了自由空间空气密度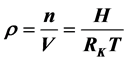 ,说明空气密度随海拔高度的升高而成倍地增加,并与温度成负相关关系。同时认为,自由空间的空气应该从压力高的地方向压力低的地方聚集,也就是海拔越高、压力越低,空气密度越会增加。由气态方程推导出空气密度计算公式,计算出12千米高度对流层顶的空气密度比标准大气压的ρ0增加了15倍,1000千米的散逸层则增加了187倍。当然,这一结论与“海拔越高空气越稀薄”的基本常识相反!这或许是因为我们忽略了天然丰度为99.985%的氕这种物质所致。因此,推论大气空间任何物质都最终都可能分(裂)解成最简单的物质--氕(H、“质子”),并在电离层失去核外电子而成为“中子”,然后“逃逸”到宇宙空间以新的方式和形式组成新的物质和星球。这也许是地球上的物质通过大气与宇宙星球进行物质交换的一个途径。
,说明空气密度随海拔高度的升高而成倍地增加,并与温度成负相关关系。同时认为,自由空间的空气应该从压力高的地方向压力低的地方聚集,也就是海拔越高、压力越低,空气密度越会增加。由气态方程推导出空气密度计算公式,计算出12千米高度对流层顶的空气密度比标准大气压的ρ0增加了15倍,1000千米的散逸层则增加了187倍。当然,这一结论与“海拔越高空气越稀薄”的基本常识相反!这或许是因为我们忽略了天然丰度为99.985%的氕这种物质所致。因此,推论大气空间任何物质都最终都可能分(裂)解成最简单的物质--氕(H、“质子”),并在电离层失去核外电子而成为“中子”,然后“逃逸”到宇宙空间以新的方式和形式组成新的物质和星球。这也许是地球上的物质通过大气与宇宙星球进行物质交换的一个途径。
关键词 :气态方程,自由空间,空气密度,星球物质

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
有人发现在高海拔地方封闭的袋子到低海拔的地方会胀!
有人解释是:因为海拔高,气压会比通常的低,而袋子里的空气体积是一定的。并用物理公式: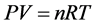 (P:气压,V:体积,n:物质的量,R:常数,T:绝对温度) [1] [2] 解释,在气压变小,其他不变的情况下,体积会变大。这就像把装空气的袋子从深水拿到浅水,袋子体积会变大一样。
(P:气压,V:体积,n:物质的量,R:常数,T:绝对温度) [1] [2] 解释,在气压变小,其他不变的情况下,体积会变大。这就像把装空气的袋子从深水拿到浅水,袋子体积会变大一样。
这样的解释看上去很有道理,但似乎忽略了一个重要因素,那就是袋子里空气的量n是一个定量,可以是空气的(摩尔)质量,也可以是空气的(氧)分子个数,而我们把这些都当成了同一个量,还看成了常量!
2. 气态方程问题的证明
设高海拔为1地,低海拔为2地,这两地的气体都应该满足气态方程:

在高海拔1地用固定容器取得气体V,运到低海拔2地,用空调保证气体是同一温度T,则: ;
;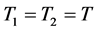 ;
;
(2) − (1)得:
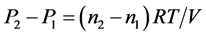
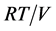 成了常数,
成了常数,
如果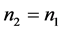 ,则
,则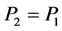 ;
;
如果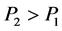 ,则
,则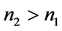 !
!
也即是,在保证气体温度不变条件下,将一定体积的气体从高海拔1地移到低海拔2地,气体的量n会随压力P的增加而增加!如果我们认为固定的容器里空气的量没有变化,那大气压还能让气体的量增加或减少?!
我们也能由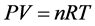 推导出空气密度
推导出空气密度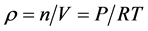 ,即是在保持温度不变时,压力越大空气的密度越大!还有人研制空气密度测量仪 [3] [4] 验证了气态方程,但这也许只是在体积固定时正确 [5] ,而在自由空间里这样的结论好像存在问题!因为气体总是从压力高的地方向压力低的地方流动,就像水总是流向低洼的地方一样。所以,自由空间里,海拔越高、压力越低,其它地方的气体就会向这里聚集,并最终达到平衡!也就是,如果两地存在压力差,则压力低的地方空气密度就会增加!
,即是在保持温度不变时,压力越大空气的密度越大!还有人研制空气密度测量仪 [3] [4] 验证了气态方程,但这也许只是在体积固定时正确 [5] ,而在自由空间里这样的结论好像存在问题!因为气体总是从压力高的地方向压力低的地方流动,就像水总是流向低洼的地方一样。所以,自由空间里,海拔越高、压力越低,其它地方的气体就会向这里聚集,并最终达到平衡!也就是,如果两地存在压力差,则压力低的地方空气密度就会增加!
3. 自由空间空气密度与海拔高度H的关系式
我们都知道海拔高度H越高,气压P越低。有资料显示海拔升高到3000千米,大气压强气压降低到10−59hp [6] [7] ,因此,压强P与海拔高度H有负相关关系。为简便起见,我们设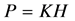 ,
,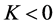 ,比如,在0~12千米的对流层,压强由1000 hp降到了250 hp,则把这段距离的K看成是−750 hp/12 km)。
,比如,在0~12千米的对流层,压强由1000 hp降到了250 hp,则把这段距离的K看成是−750 hp/12 km)。
这时,气态方程可写成:
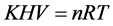 ,
,
令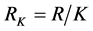
则:
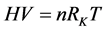 (3)
(3)
方程(3)也许可以称为“自由空间气态方程”!
很明显,自由空间空气密度
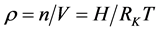 (4)
(4)
或,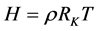 (4)’
(4)’
即是,大气中任一点的空气密度ρ与该点的海拔高度H成正比,与温度T成反比!
4. 空气密度变化量Δρ的计算公式
设,标准大气压时的海拔高度为H0,温度为T0,分子密度为ρ0,和自由空间任一高度H、温度为T,空气密度为ρ,由(4)’可得,

(6) ÷ (5)得:

即是:
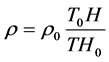 (7)
(7)
当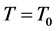 时,
时,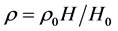 ,
,
即是温度不变时,气体密度与海拔高程成正比,而与其它系数无关;
当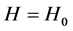 时,
时,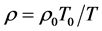 ,
,
即是高度不变时,气体密度与温度成反比,而与其它系数无关!
方程(7)表明,只要确定了标准大气的空气密度ρ0、高度H0和温度T0,就可以计算太空中任一高度H和在温度T时的空气密度,而不需要其它任何系数。因此,公式(7)可以称之为“自由空间空气密度计算公式”!
设: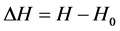 ;
; ,由公式(7)可得空气密度的变化量为:
,由公式(7)可得空气密度的变化量为:

即得,
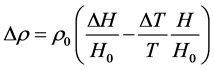 (8)
(8)
其中,H为海拔高度,T为绝对温度。
我们将(8)式称之为“自由空间空气密度变化量”计算公式。
在不考虑温度变化的影响时(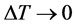 ),
),
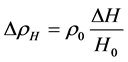 (8)’
(8)’
即是空气密度变化量随海拔成倍升高而成倍增加。比如,海拔由1千米升到5千米,则空气密度增加4倍!
温度对气体密度影响的表达式为:
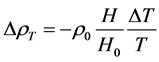 (8)’’
(8)’’
即是,温度对气体密度的影响取决于温度是升高还是降低,温度升高使气体密度减小、温度降低使气体密度增大。而减小或增大的量取决于温度的变化率(ΔT/T),与海拔升高的倍数(H/H0)的乘积。
5. 自由空间空气密度的计算
相关数据表明大气的层状 [6] 是与地球形状相关的同心椭球体(图1) [7] 。设标准大气P0 = 103百帕 [7] ,T0 = 288 K (15℃) [7] ,H0 = 1千米,气体密度为ρ0,根据公式(8)可以计算出大气层在不同高度和温度下的气体密度升高的倍数(表1、图1)。从地面开始到中间层顶(87千米高度),气体密度逐渐增加了146倍,进入暖层后减小到95倍,到散逸层后一直持续增加到187倍以上。
6. 自由空间空气密度的讨论
1) 自由空间的气体(物质)应该从压力高的地方向压力低的地方流动和聚集,就像水流向洼地形成湖
Table 1. Changes of gas density at different altitudes
表1. 不同海拔高度气体密度变化一览表
注:表中数据由大气垂直分层图(高举等,2016)估计得来。
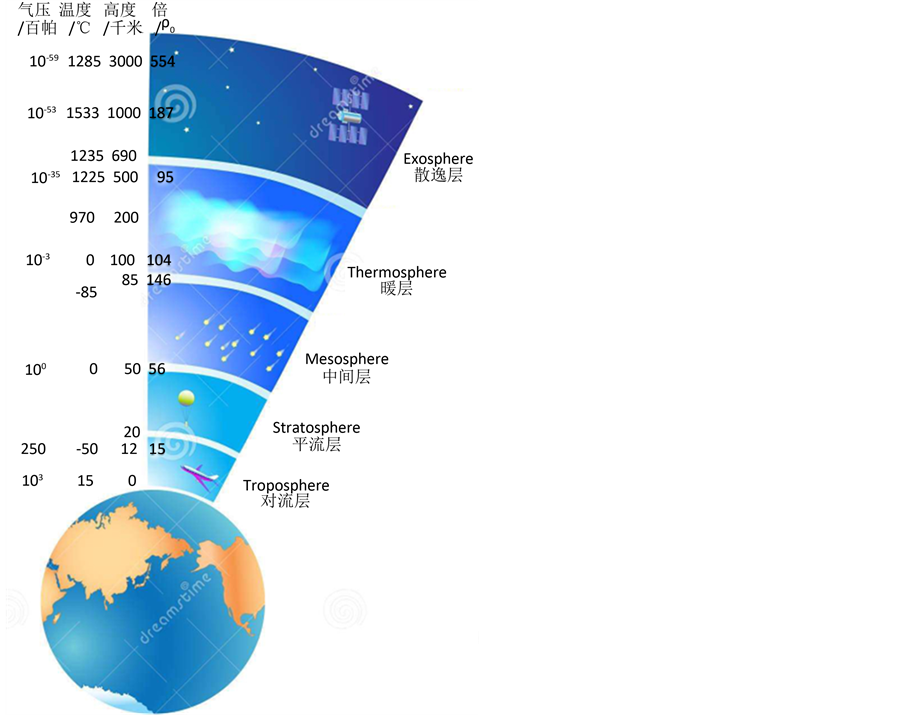
Figure 1. Stratification and density change of atmosphere. (Baidu: Dreamstime.com; Tanmu, 2016, modification)
图1. 大气的分层和密度变化。(百度自Dreamstime.com;檀木,2016,有修改)
泊一样,洼地面积越大、越深,汇聚的水越多。因此,大气空间里气体物质应该向压力低的地方流动。
2) 自由空间的海拔越高、气压越低、气体越轻,气体的“分子量”越小、“分子”个数越多,所以气体分子密度越大。比如:2H2O (气态)→2H2↑ + 2O2↑,2个气态水分子在自由空间里应该分解成2个氢气分子和2个氧气分子,其分子个数增加了一倍!
3) P = KH建立在大气压力随海拔的升高而减小的基础上,不同高度的K值是不一样的,所以,这种线性关系只能在一定的高度范围有效,无限推算高度当然存在问题。精确计算不同海拔高度的空气密度最简单的办法就是测得温度变化层的空气密度值。
4) 大雁迁徙在10千米高度(没有缺氧反应),或许是因为海拔越高、温度越低、气体密度越大,空气浮力越大所致。
7. 结论和推论
很明显,以上讨论都与常识相反!或许,自由空间的气体最终都分解成了氕(H)这种物质。我们可以把任何物质的原子(元素)都可以看成是不同个数的质子和中子的一种组合,也就是,看成不同个数的氘(D)的组合。比如:一个氮原子可以看成是7氘原子组成,即是,1N = 7D;同样地,1O = 8D。这样,空气中的气体最终都“分解”成氘,进而“衰变”成氕(H)。
因此认为:
1) 空气密度需要考虑天然丰度为99.985%的氕 [8] [9] [10] ,而这种物质的“分子”很小,甚至可以从许多容器中毫无踪迹地逸出。
2) 地球表面升起的水蒸气应该分解成了氢气和氧气。氧气直接融入空气,而氢气与太空中的(臭)氧,在雷电作用下形成雨。
3) 大气中可能富含我们日常生活所需的多种气体。在不同高度和温度空间可能有不同的气体,包括能源气体的存在。
4) 高空大气中的任何气体最终分(裂)解成单个原子H(氕),并在电离层由于密度的增加和空间的减少而失去核外电子,最终成为中子。
5) 从大气层“逃逸”的“质子”进入宇宙空间以新的方式和形式组成新的物质和星球,地球物质通过这种形式与宇宙星球进行物质交换。
文章引用
邵行来,王威,周耀明. 理想气体状态方程的问题和思考
Problems and Thoughts on the State Equation of Ideal Gas[J]. 天文与天体物理, 2017, 05(02): 15-20. http://dx.doi.org/10.12677/AAS.2017.52003
参考文献 (References)
- 1. 张维善. 物理普通高中标准试验教科书•选修3-3(第三版)[M]. 北京: 人民教育出版社, 2010: 23-24.
- 2. 傅献彩, 沈文霞, 姚天扬, 候文华. 物理化学(下册第五版)[M]. 北京: 高等教育出版社, 2007: 313-316.
- 3. 王旭, 崔敏, 周琪等. 空气密度测量仪的研制与测试研究[J]. 物理实验, 2013, 33(12): 41-44.
- 4. 鲁佩用. “大气压强”实验创新设计[J]. 物理教学探讨(中学教学教研专辑), 2014, 32(3): 67-68.
- 5. 王子佳. 适用理想气态方程计算瓦斯压强的条件探讨[J]. 煤炭技术, 2005, 24(10): 120-121.
- 6. 王安强. 图文结合理解大气环流过程及原理[J]. 考试周刊, 2013(23): 126-127.
- 7. 檀木. 中学地理图文讲解指导地图测(第十三版)[M]. 济南: 山东地图出版社, 2016: 22.
- 8. 杨晓志. 浅谈高温高压实验地球科学: 方法和应用[J]. 矿物岩石地球化学通报, 2015, 34(3): 509-525.
- 9. 蒋昌勇, 陈静, 曹小华. 氕氘比CH/CD的四极质谱计测量[J]. 原子能科学技术, 2002, 36(4/5): 462-465.
- 10. 郑军卫, 张志强, 赵纪东. 21世纪地球科学研究的重大科学问题[J]. 地球科学进展, 2008, 23(12): 1260-1267.
