Astronomy and Astrophysics
Vol.06 No.01(2018), Article ID:23371,10
pages
10.12677/AAS.2018.61001
Numerical Study on the Species of Transfer Orbit in the Circular Restricted Three-Body Problem
Yu Huang, Fan Lin, Yiqing Shen, Ruifang Wang, Fabao Gao*
College of Mathematical Science, Yangzhou University, Yangzhou Jiangsu

Received: Dec. 19th, 2017; accepted: Jan. 3rd, 2018; published: Jan. 10th, 2018

ABSTRACT
Based on the dynamical equations of spatial circular restricted three-body problem, the bifurcation diagram of the system with the mass ratio as the bifurcation parameter is demonstrated, and it is found that when the masses of the two main bodies are considerable equivalent (i.e., the mass ratio is around 0.5), the third body’s dynamic behavior is more complicated than at other mass ratios. When the mass ratio is in the interval (0.4, 0.6), we further simulate 32,000 transfer orbits and make a brief classification of the found orbits.
Keywords:CR3BP, Bifurcation Diagram, Transfer Orbit, Interplanetary Interchange Station
圆型限制性三体问题中转移轨道类型的数值研究
黄宇,林帆,沈怡晴,王瑞芳,高发宝*
扬州大学数学科学学院,江苏 扬州

收稿日期:2017年12月19日;录用日期:2018年1月3日;发布日期:2018年1月10日

摘 要
基于空间圆型限制性三体问题的动力学方程,我们首先数值模拟了系统以质量比为参数的分岔图,发现两个主天体的质量相当(即质量比率在0.5附近)时,第三体的动力学行为较其它质量比下更为复杂。当质量比在区间(0.4, 0.6)时,我们进一步数值模拟了32,000条转移轨道,并将发现的轨道作了简要的分类。
关键词 :圆型限制性三体问题,分岔图,转移轨道,星际换乘站

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
当三体系统中所研究的第三个天体的质量与其他两个天体的质量相比,其质量小到可以忽略时﹐则称此系统为限制性三体问题。一般将此小质量的天体称为无限小质量体,或简称小天体;两个大质量的天体称为有限质量体。因为小天体的质量很小,可不考虑它对两个有限质量体的吸引力,即它不影响两个有限质量体的运动。于是,对两个有限质量体的运动状态的讨论,仍为二体问题,其轨道为以它们的质量中心为焦点的圆锥曲线 [1] [2] [3] 。
由于限制性三体问题还未发现有解析解,很多研究者通过数值模拟等方法给出了大量的数值结果。例如,Broucke [4] 在1968年美国喷气推进实验室(JPL)一份科技报告中,数值地研究了地-月质量比下限制性三体问题的一类平面对称周期轨道,并通过数值积分得到了1811条周期轨道并将其划分成10种不同的类别。2000年,法国数学家Chenciner和美国数学家Montgomery [5] 通过变分法惊奇地发现平面上等质量的三个质点存在8字型周期轨道,使得三体问题的数值解在一百年来有了新的突破。2013年,塞尔维亚物理学家Šuvakov和Dmitrašinović [6] 运用计算机模拟,先从平面等质量的圆型限制性三体问题的一个已知特解开始,然后不断地对其初始条件进行微小的调整,最终发现了13族新的特解。2017年,上海交通大学廖世俊课题组通过超级计算机对不等质量的平面三体问题数值模拟的1600万条轨道进行测试,发现了令人兴奋的1349条周期轨道 [7] [8] [9] 。
本文主要运用MATLAB数值研究空间圆型限制性三体问题的分岔图,并进一步数值模拟天体质量比率 在0.4到0.6之间的转移轨道,以及质量比为0.499时不同的初值条件对转移轨道的影响。最后,通过对数值模拟得到的32,000条轨道进行对比分析,我们将对其进行简单的分类。
2. 限制性三体系统建模及分析
我们首先介绍两个常用坐标系:质心惯性坐标系 和质心转动坐标系 。质心惯性坐标系 是由一个探测器或小天体 ,两个大天体 和 组成的系统,坐标系的原点 与 和 的质心重合(图1),其中 平面是两个大天体的轨道平面, 和 围绕它们的公共质心作圆周运动,探测器或小天体 只受到 和 的引力作用, 轴由 指向 , 轴与之垂直并满足右手坐标系(默认 轴垂直于轨道平面 ),三个天体 、 和 的质量分别为 、 和 ,且 。
假设 为 和 的连线绕其质心转过的角度,引入系统的质量比率 且 ,则两个大天体 和 到其公共质心的无量纲距离分别为 和 ,故此三体问题中的无量纲方程组为 [10] :
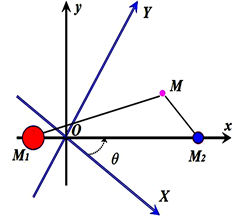
Figure 1. Coordinate system
图1. 坐标系
3. 系统的分岔图及转移轨道的数值研究
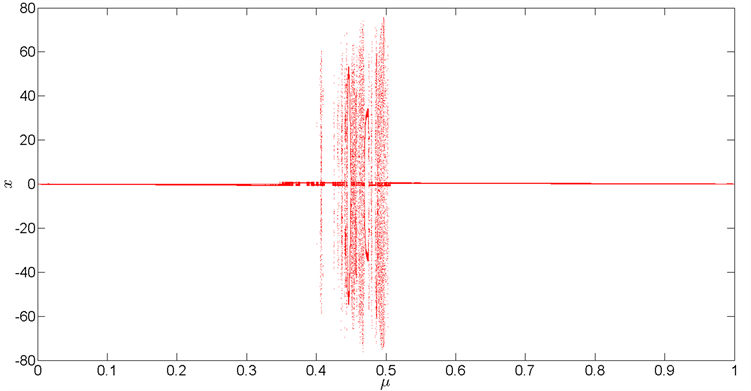
在初值为 ,步长为1.0E−5的条件下,通过MATLAB2011a对此系统进行数值模拟,我们得到系统轨道分岔图(图2(a)及2(b)),由图2(a)不难发现当系统的质量比在区间 时,系统的动力学行为较为复杂。
不失一般性,当 时,我们对系统的转移轨道进行数值模拟,得到20000条第三体的转移轨道。通过图形分析可以发现:当 的取值在0.4与0.503之间时,转移轨道的动力学行为的变化较丰富(图3~图6),这与分岔图(图2(b))的结果也相吻合。此时,转移轨道主要呈现为以相类似的轨线重复飞掠两主天体(图3),或以螺旋轨线环绕两主天体并逐渐向深空发散(图4),或从初始位置出发经过简单的转移轨道(如抛物线型、花瓣型等)到达其中一主天体附近,然后以螺旋轨线环绕此单个主天体逐渐发散(图5),亦或以8字型轨线环绕其中一主天体后转移到另一主天体附近继续以8字型轨线环绕(图6);当 的取值在0.503与0.6之间时,系统的转移轨道相对单调,多呈现为类似于图5的形态。
由于质量比在0.5附近时第三体的动力学行为较为复杂,下面针对 固定为0.499时的系统,我们对不同的初始位置进行了数值模拟,分别改变前面初始条件中三个关于初始位置的取值,得到了6000条转移轨道。转移轨道主要呈现为在某一主天体附近的花状环绕型(图7),或以花瓣状轨道环绕其中一主天体后转移到另一主天体附近继续以花瓣状轨道环绕(图8),或以螺旋轨线环绕两主天体并逐渐向深空发散(图9),或以螺旋轨线围绕一个主天体展开(图10),或以蝴蝶轨线环绕一个主天体(图11),亦或以8字型轨线环绕某个主天体(图12)。
 (a)
(a)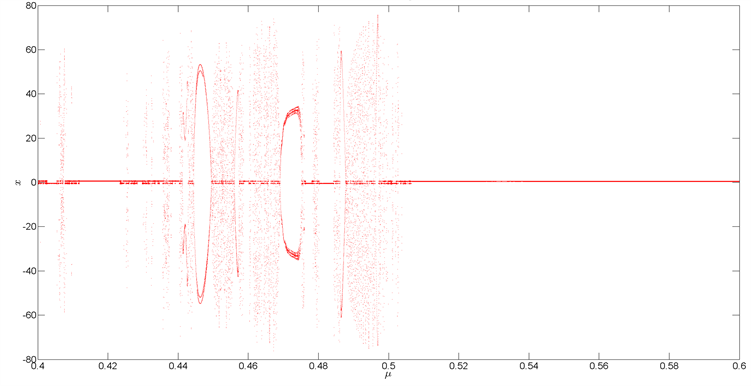 (b)
(b)
Figure 2. (a) Bifurcation diagram for ; (b) Bifurcation diagram for
图2. (a) 时的分岔图; 时的分岔图
接下来我们将研究不同初始速度下的转移轨道,分别改变前面初始条件中三个关于初始速度的取值,数值模拟得到6000条转移轨道。通过对转移轨道的筛选分析,我们发现虽然轨道的具体形状不同(图13-图16),但是所得结果不外乎前面的几种情形,这里不再赘述。
4. 结论
本文首先通过数值模拟给出了圆型限制性三体问题关于质量比的分岔图,发现当两个天体的质量相
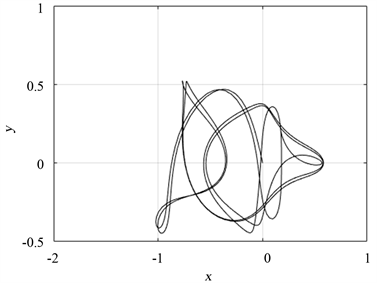
Figure 3. Mass ratio of
图3. 质量比
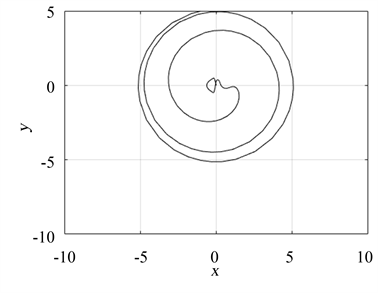
Figure 4. Mass ratio of
图4. 质量比
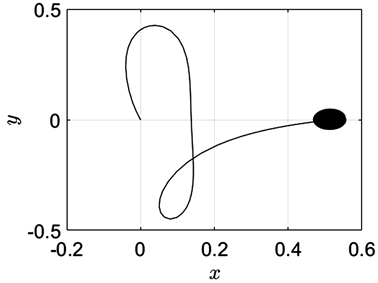
Figure 5. Mass ratio of
图5. 质量比
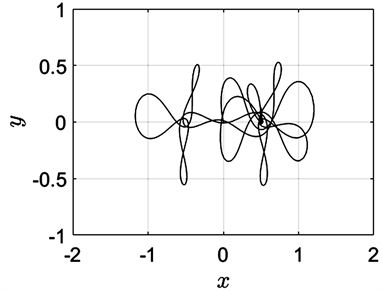
Figure 6. Mass ratio of
图6. 质量比
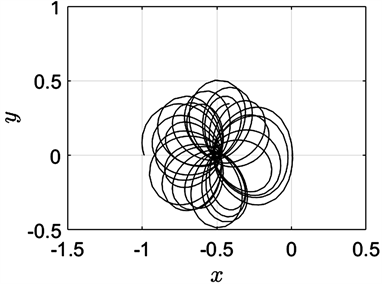
Figure 7. The initial value in the X direction is −0.986
图7. X方向的初值为−0.986
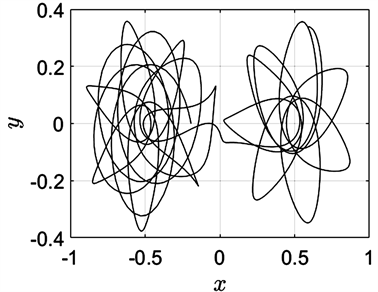
Figure 8. The initial value in the X direction is −0.193
图8. X方向的初值为−0.193
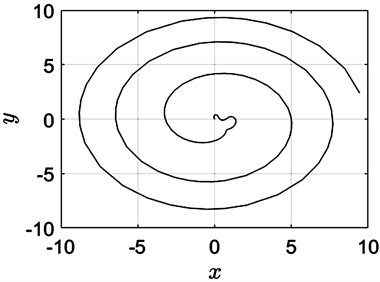
Figure 9. The initial value in the X direction is −0.004
图9. X方向的初值为−0.004
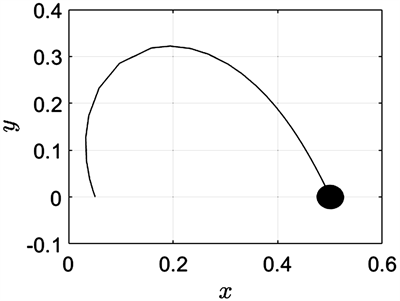
Figure 10. The initial value in the X direction is 0.051
图10. X方向的初值为0.051
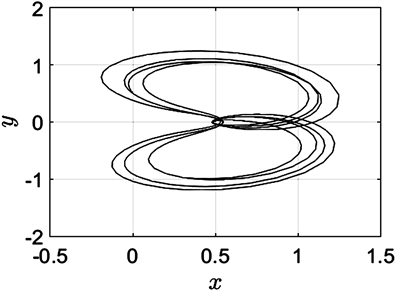
Figure 11. The initial value in the Y direction is 0.515
图11. Y方向的初值为0.515
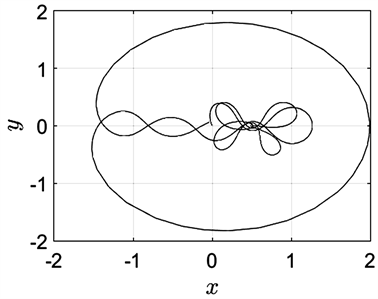
Figure 12. The initial value in the Z direction is −0.107
图12. Z方向的初值为−0.107
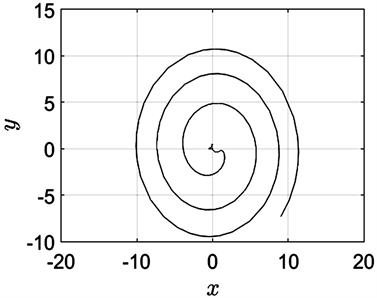
Figure 13. The initial velocity in the X direction is −0.48
图13. X方向的初始速度为−0.48
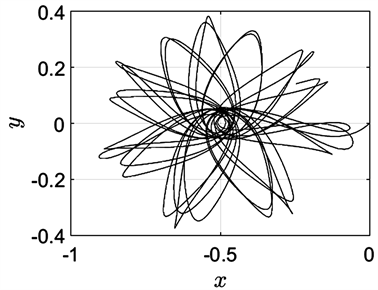
Figure 14. The initial velocity in the Y direction is −0.3
图14. Y方向的初始速度为−0.3
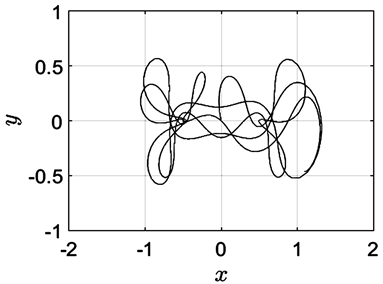
Figure 15. The initial velocity in the Z direction is −0.44
图15. Z方向的初始速度为−0.44
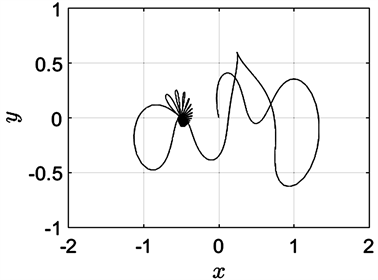
Figure 16. The initial velocity in the Z direction is −0.5
图16. Z方向的初始速度为−0.5
当时,第三体的动力学行为较为丰富;其次,我们对质量比在区间(0.4, 0.6)时下的系统进行了大量的数值模拟,共计得到32,000条转移轨道,并通过对转移轨道的逐条分析对比,我们发现虽然这些轨线形态各异,但是从它们环绕主天体的方式以及演绎的形状来看,可以将它们大体分成以花瓣状、螺旋状、8字型等形状的轨线环绕某一主天体或者两个主天体等几类转移轨道。当然,我们还发现在不同的质量比、初始位置、初始速度下,很多的转移轨道是类似的,这或许是由不同分量的初始位置和速度的取值之间具有一定的相关性引起的。
由于三体问题的高度非线性,我们期望接下来的工作能够就更多的转移轨道,从统计学的角度研究满足我们所关注的转移轨道的初始条件之间的相关性,统计出概率意义上的飞掠型转移轨道的初始条件集,类似于JPL的星际高速公路理论,我们暂且称这些初始条件集为“星际换成站”,这样第三体将能从这些“站内点”出发,飞掠其他星球。
基金项目
国家自然科学基金项目(Nos.: 11672259, 11302187, 11571301);国土资源部公益性项目(No.: 201411007);扬州大学大学生科技创新基金项目(No.: x20160247);江苏高校品牌专业建设工程资助项目(No.: PPZY2015B109)。
文章引用
黄 宇,林 帆,沈怡晴,王瑞芳,高发宝. 圆型限制性三体问题中转移轨道类型的数值研究
Numerical Study on the Species of Transfer Orbit in the Circular Restricted Three-Body Problem[J]. 天文与天体物理, 2018, 06(01): 1-10. http://dx.doi.org/10.12677/AAS.2018.61001
参考文献 (References)
- 1. 刘暾, 赵钧. 空间飞行器动力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003.
- 2. Curtis, H.D. (2005) Orbital Mechanics for Engineering Students. Elsevier, Amsterdam.
- 3. 刘林, 侯锡云. 深空探测器轨道力学[M]. 北京: 电子工业出版社, 2012.
- 4. Broucke, R.A. (1968) Periodic Orbits in the Restricted Three-Body Problem with Earth-Moon Masses, Jet Propulsion Laboratory. Technical Report, 82-1168.
- 5. Chenciner, A. and Montgomery, R. (2000) A Remarkable Periodic Solution of the Three Body Problem in the Case of Equal Masses. Annals of Mathematics, 152, 881-901.
https://doi.org/10.2307/2661357 - 6. Šuvakov, M. and Dmitrašinović, V. (2013) Three Classes of Newtonian Three-Body Planar Periodic Orbits. Physical Review Letters, 110, 114301.
https://doi.org/10.1103/PhysRevLett.110.114301 - 7. Crane, L. (2017) Three-Body Problem Gets 1000 Solutions. NewScientist, 235, 14 p.
https://doi.org/10.1016/S0262-4079(17)31908-5 - 8. Li, X.M., Jing, Y.P. and Liao, S.J. (2017) The 1223 New Periodic Orbits of Planar Three-Body Problem with Unequal Mass and Zero Angular Momentum. arXiv:1709.04775v1
- 9. Li, X.M. and Liao, S.J. (2017) More Than Six Hundred New Families of Newtonian Periodic Planar Collisionless Three-Body Orbits. Science China Physics, Mechanics & Astronomy, 60, 129511.
https://doi.org/10.1007/s11433-017-9078-5 - 10. 高发宝. 深空探测中非线性动力学及周期轨道的研究[D]: [博士学位论文]. 北京: 北京工业大学, 2012.
NOTES
*通讯作者。