Dynamical Systems and Control
Vol.05 No.02(2016), Article ID:17361,7
pages
10.12677/DSC.2016.52005
On Synchronization of 5D Hyperchaotic System and 3D Chaotic System with Variable Coefficient
Hong Niu
College of Electronic Information and Automation, Tianjin University of Science & Technology, Tianjin

Received: Mar. 17th, 2016; accepted: Apr. 15th, 2016; published: Apr. 18th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the 3D chaotic system and the 5D hyperchaotic system are synchronized via the center translation method, where the variable coefficient in the nonlinear part of the 3D chaotic system is taken as the uncertainty in the synchronization. The center of the state variables of the response 3D chaotic system is translated to the assigned state variables of the drive 5D hyperchaotic system, such that the model of the error system is the same as that of the response system. Thus, synchronization of different systems is converted to stability control of the error system. This method can effectively simplify the design procedure for synchronization controller, and it can be applied to the study of drive system with uncertainty, so long as the synchronized state variables of the drive system and their derivatives are known or can be estimated by state observer.
Keywords:Synchronization via Center Translation Method, Synchronization of Different Systems, Nonlinear Control, Uncertainty

具有可变系数的三维混沌系统与五维超混沌系统的同步问题研究
牛弘
天津科技大学电子信息与自动化学院,天津

收稿日期:2016年3月17日;录用日期:2016年4月15日;发布日期:2016年4月18日

摘 要
本文基于中心平移同步法,研究非线性部分具有可变系数,即非线性部分系数具有不确定性的三维混沌系统与五维超混沌系统的同步问题。通过将响应三维混沌系统状态变量的中心平移至驱动五维超混沌系统的指定状态变量,将异结构系统的状态同步问题转化为与响应系统模型相同的误差系统的稳定性控制问题。该方法可有效简化同步控制器的设计过程,并可应用于驱动系统模型具有不确定性但其需同步状态及其导数已知或可通过状态观测器估算的同步问题研究中。
关键词 :中心平移同步法,异结构同步,非线性控制,不确定性

1. 引言
对于异结构系统的混沌同步或超混沌同步研究,如文献 [1] [2] 中所示,结构补偿还是相对常用的设计思路。结构补偿的作用是补偿响应系统与驱动系统在结构上的差异,以使两系统在同步控制器的作用下达到同步。如何设计出合适的结构补偿器值得研究。本文作者于文献 [3] 中提出中心平移同步法,该法通过将响应系统状态变量的中心平移至驱动系统需同步的状态变量,将结构补偿器的设计过程隐含于误差系统的建模中,将异结构系统的状态同步问题转化为非线性系统的稳定性控制问题。该方法为结构补偿器的设计提供了一种新思路。
对于具有不确定性系统的混沌同步或超混沌同步研究,如文献 [4] - [7] 中所示,自适应同步法仍是主流方法。文献 [8] 将扩张状态观测器和自抗扰控制器(ADRC)应用于混沌系统的观测和控制。考虑到扩张状态观测器不依赖于对象模型,因此自抗扰控制也可应用于具有不确定性系统的混沌同步研究中,如文献 [9] 中所示。在具有可变系数的三维混沌系统与五维超混沌系统的同步中,本文将三维混沌系统中的可变系数作为具有不确定性的参数,基于中心平移同步法设计同步控制器,使三维混沌系统的状态变量在可变参数的变化范围内均可与五维超混沌系统中的指定状态变量达到同步。该方法可应用于驱动系统模型具有不确定性但需同步状态及其导数可测和(或)响应系统模型确定但其包含变化范围已知的不确定参数的同步问题研究中。
2. 误差系统建模与同步控制器设计
2.1. 五维超混沌系统
五维超混沌系统的模型如下所示 [10]
 (1)
(1)
其中,a = 23,b = 3,c = 18,m = 12,h = 4。
令五维超混沌系统(1)的初值为 ,此时系统的Lyapunov指数分别为
,此时系统的Lyapunov指数分别为 ,
,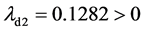 ,
,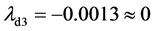 ,
, ,
, ,有两个大于0的Lyapunov指数,说明系统是超混沌的。
,有两个大于0的Lyapunov指数,说明系统是超混沌的。
2.2. 三维混沌系统
三维混沌系统的模型如下所示 [11]
 (2)
(2)
其中,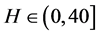 为可变系数。系统(2)随H变化的Lyapunov指数谱如图1中所示。当
为可变系数。系统(2)随H变化的Lyapunov指数谱如图1中所示。当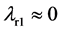 ,
, 时,系统(2)处于周期运动状态;当
时,系统(2)处于周期运动状态;当 ,
,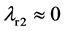 ,
, 时,系统(2)处于混沌运动状态。
时,系统(2)处于混沌运动状态。
2.3. 误差系统建模
令同步误差为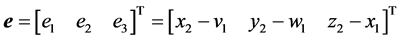 ,根据文献 [3] ,误差系统的模型可表示为
,根据文献 [3] ,误差系统的模型可表示为
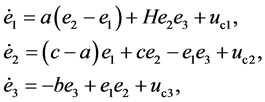 (3)
(3)
未加入同步控制器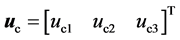 时,系统(3)等价于将三维混沌系统(2)中的状态变量
时,系统(3)等价于将三维混沌系统(2)中的状态变量 的中心平移至驱动系统(1)的指定状态变量
的中心平移至驱动系统(1)的指定状态变量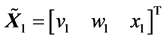 。现只需设计同步控制器
。现只需设计同步控制器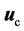 ,使同步误差
,使同步误差 全局渐近收敛于原点,即可使三维响应混沌系统(2)的状态变量在
全局渐近收敛于原点,即可使三维响应混沌系统(2)的状态变量在 内无论处于周期运动状态或是混沌运动状态,均可与五维驱动超混沌系统(1)中的指定状态变量达到同步。
内无论处于周期运动状态或是混沌运动状态,均可与五维驱动超混沌系统(1)中的指定状态变量达到同步。

Figure 1. Lyapunov exponent spectrum of the response system (2) versus increasing H
图1. 响应系统(2)随H变化的Lyapunov指数谱
2.4. 同步控制器设计
文献 [12] 中针对形如误差系统(3)的具有可变系数的三维混沌系统的稳定性控制问题,通过先对被控系统进行线性化,消去可变系数,求出使被控系统渐近稳定的控制参数范围,而后构造Lyapunov函数,基于线性化所得控制参数范围,采用试探法,求解可使被控系统在可变系数范围内全局渐近稳定的控制参数,有效的简化了控制参数的求解过程,且所得控制器可以是线性的。由于误差系统(3)与文献 [12] 中被控系统的模型完全相同,故可将同步控制器 设计为
设计为
 。 (4)
。 (4)
将式(4)代入式(3),取径向无界的正定函数
 ,
,
作为误差系统(3)的Lyapunov函数,其导数为
 , (5)
, (5)
其中,矩阵Q的各阶顺序主子式分别为

要使矩阵Q是负定的,即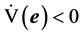 ,只需
,只需 。文献 [12] 中已证明,当
。文献 [12] 中已证明,当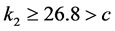 时,在
时,在 内,
内, ,此时矩阵Q是负定的,则
,此时矩阵Q是负定的,则 。又因为
。又因为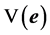 是径向无界的,则误差系统(3)在原点处是全局渐近稳定的。现取
是径向无界的,则误差系统(3)在原点处是全局渐近稳定的。现取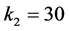 ,则同步控制器
,则同步控制器 可表示为
可表示为
 (6)
(6)
3. 数值仿真
中心平移同步法的实质是将不易直观设计出的结构补偿器
 , (7)
, (7)
及同步控制器 加入到三维混沌系统(2)中。令五维超混沌系统(1)作为驱动系统,可得响应系统的模型为
加入到三维混沌系统(2)中。令五维超混沌系统(1)作为驱动系统,可得响应系统的模型为
 (8)
(8)
式(8)与式(3)等价。
定义1 加入同步控制器与结构补偿器后,响应系统(8)的Lyapunov指数称为条件Lyapunov指数 [13] [14] 。
定理1(同步定理) 只有当响应系统(8)的所有条件Lyapunov指数都是负值时,才能达到响应系统(8)与驱动系统(1)的同步 [13] [14] 。
令响应系统(8)的初值为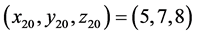 ,将式(6)及式(7)代入式(8)中,可得响应系统(8)随H变化的条件Lyapunov指数谱如图2中所示。从图2中可以看出,不同H值下系统(8)的条件Lyapunov指数均为负值,说明在
,将式(6)及式(7)代入式(8)中,可得响应系统(8)随H变化的条件Lyapunov指数谱如图2中所示。从图2中可以看出,不同H值下系统(8)的条件Lyapunov指数均为负值,说明在 内,响应系统(8)与驱动系统(1)中的对应状态变量可以达到同步。
内,响应系统(8)与驱动系统(1)中的对应状态变量可以达到同步。
4. 算例
令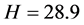 。未加入同步控制器
。未加入同步控制器 和结构补偿器
和结构补偿器 时,响应系统(8)的Lyapunov指数分别为
时,响应系统(8)的Lyapunov指数分别为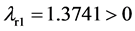 ,
, ,
, ,说明系统是混沌的。此时响应系统(8)与驱动系统(1)各对应状态变量的误差及同步曲线分别如图3(a)和图3(b)中所示。图中横轴t表示式(8)的求解区间,为一无量纲量,后文各图中横轴t的定义与此处相同。从图3中可以看出,状态变量
,说明系统是混沌的。此时响应系统(8)与驱动系统(1)各对应状态变量的误差及同步曲线分别如图3(a)和图3(b)中所示。图中横轴t表示式(8)的求解区间,为一无量纲量,后文各图中横轴t的定义与此处相同。从图3中可以看出,状态变量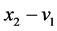 、
、 、
、 的差异很大。
的差异很大。
现将式(6)及式(7)代入式(8)中,可得响应系统(8)的条件Lyapunov指数分别为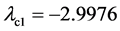 ,
,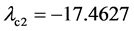 ,
,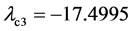 ,均为负值,说明响应系统(8)与驱动系统(1)中的对应状态变量可以达到同步。
,均为负值,说明响应系统(8)与驱动系统(1)中的对应状态变量可以达到同步。
加入同步控制器 和结构补偿器
和结构补偿器 后,响应系统(8)与驱动系统(1)各对应状态变量的误差及同步曲线分别如图4(a)和图4(b)中所示。从图4中可以看出,误差
后,响应系统(8)与驱动系统(1)各对应状态变量的误差及同步曲线分别如图4(a)和图4(b)中所示。从图4中可以看出,误差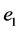 、
、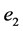 、
、 分别渐近收敛于0,且收敛速度很快,
分别渐近收敛于0,且收敛速度很快,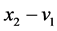 、
、 、
、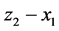 均可以很好的达到同步。这说明将中心平移同步法应用于对异结构系统指定状态变量间的同步控制是可行的与有效的。
均可以很好的达到同步。这说明将中心平移同步法应用于对异结构系统指定状态变量间的同步控制是可行的与有效的。

Figure 2. Sub-Lyapunov exponent spectrum of the response system (8) versus increasing H
图2. 响应系统(8)随H变化的条件Lyapunov指数谱

 (a) (b)
(a) (b)
Figure 3. Error and synchronization curves of the corresponding state variables of the response and the drive systems before adding uc and us to the response system: (a) Error curves; (b) Synchronization curves
图3. 未加入uc和us时响应系统与驱动系统对应状态变量的误差及同步曲线:(a) 误差曲线;(b) 同步曲线
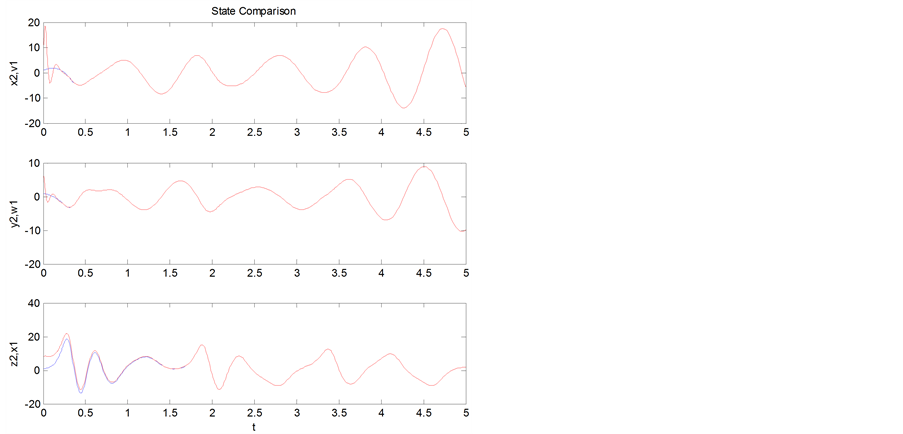
 (a) (b)
(a) (b)
Figure 4. Error and synchronization curves of the corresponding state variables of the response and the drive systems after adding uc and us to the response system: (a) Error curves; (b) Synchronization curves
图4. 加入uc和us后响应系统与驱动系统对应状态变量的误差及同步曲线:(a) 误差曲线;(b) 同步曲线
5. 中心平移同步法的优点
中心平移同步法的实质是将结构补偿器的设计过程隐含在误差系统的建模过程中,将混沌同步问题转化为非线性系统的稳定性控制问题。因此无需确定驱动系统的模型,只需驱动系统中各需同步状态变量及其导数已知或可通过状态观测器估算,即可通过搭建结构已知的响应系统模型完成对同步控制器的设计以及对驱动系统中需同步状态变量的同步跟踪。这有效的消除了驱动系统中的不确定性对同步控制器设计的影响。
6. 结论
本文基于中心平移同步法,通过将响应系统中待同步状态变量的中心平移至驱动系统中的指定状态变量,构造误差系统,使误差系统与响应系统具有相同的模型结构,这样便可将异结构系统的状态同步问题转化为非线性系统的稳定性控制问题。中心平移同步法可有效简化同步控制器中控制参数的求解过程。本文通过数值仿真验证了该同步方法的可行性与有效性。该方法为具有不确定性的异结构混沌、超混沌系统的同步问题提供了一种新的解决思路。但该方法的电路可实现性需进一步研究,即如何在不构建结构补偿器的基础上将中心平移同步法直接应用于待同步系统的电路实现中有待解决。
文章引用
牛 弘. 具有可变系数的三维混沌系统与五维超混沌系统的同步问题研究
On Synchronization of 5D Hyperchaotic System and 3D Chaotic System with Variable Coefficient[J]. 动力系统与控制, 2016, 05(02): 41-47. http://dx.doi.org/10.12677/DSC.2016.52005
参考文献 (References)
- 1. Liu, Y.Z., Jiang, C.S., Lin, C.S., et al. (2007) Chaos Synchronization between Two Different 4D Hyperchaotic Chen Systems. Chinese Physics, 16, 660-665. http://dx.doi.org/10.1088/1009-1963/16/3/017
- 2. 牛弘, 张国山. 一类具有可变系数的混沌系统的同步[J]. 物理学报, 2013, 62(13): 105-115.
- 3. Niu, H., Zhang, G.S. and Wang, J.K. (2014) Chaos Synchronization of Chua’s Circuit and Lorenz System Based on Strictly Positive Realness. Proceedings of the 33th Chinese Control Conference, CCC 2014, Nanjing, 28-30 July 2014, 1972-1976. http://dx.doi.org/10.1109/chicc.2014.6896932
- 4. Salarieh, H. and Shahrokhi, M. (2008) Adaptive Synchroniza-tion of Two Different Chaotic Systems with Time Varying Unknown Parameters. Chaos, Solitons & Fractals, 37, 125-136. http://dx.doi.org/10.1016/j.chaos.2006.08.038
- 5. Zhu, C.X. (2009) Adaptive Synchronization of Two Novel Different Hyperchaotic Systems with Partly Uncertain Parameters. Applied Mathematics and Computation, 215, 557-561. http://dx.doi.org/10.1016/j.amc.2009.05.026
- 6. Fu, G.Y. and Li, Z.S. (2010) Adaptive Synchronization of a Hyperchaotic Lü System Based on Extended Passive Control. Chinese Physics B, 19, 060505-1-5.
- 7. Kuntanapreeda, S. and Sangpet, T. (2012) Synchronization of Chaotic Systems with Unknown Pa-rameters Using Adaptive Passivity-Based Control. Journal of the Franklin Institute, 349, 2547-2569. http://dx.doi.org/10.1016/j.jfranklin.2012.08.002
- 8. 张文革, 韩京清. 一类混沌系统的状态观测与控制[J]. 控制与决策, 2000, 15(3): 301-304.
- 9. 张国山, 李思瑶, 王江. 基于自抗扰控制的2个耦合神经元间的混沌同步[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(3): 263-268.
- 10. 牛弘. 混沌及超混沌系统的分析、控制、同步与电路实现[D]: [博士学位论文]. 天津: 天津大学, 2014.
- 11. 张国山, 牛弘. 一个基于Chen系统的新混沌系统的分析与同步[J]. 物理学报, 2012, 61(11): 137-147.
- 12. 牛弘. 具有可变系数的三维混沌系统的稳定性控制与电路实现[J]. 动力系统与控制, 2016, 5(1): 31-40.
- 13. Pecora, L.M. and Carroll, T.L. (1990) Synchronization in Chaotic Systems. Physical Review Letters, 64, 821-824. http://dx.doi.org/10.1103/PhysRevLett.64.821
- 14. 刘秉正, 彭建华. 非线性动力学[M]. 北京: 高等教育出版社, 2007.