Dynamical Systems and Control
Vol.06 No.02(2017), Article ID:20311,8
pages
10.12677/DSC.2017.62005
Pseudospectral Mesh Refinement Algorithm Based on Density Function and Its Application
Liying Wang1, Jie Huang2, Gang Zhang3
1Institute of Systems Science and Mathematics, Naval Aeronautical and Astronautical University, Yantai Shandong
2Naval Aeronautical and Astronautical University, Qingdao Branch, Qingdao Shandong
3Naval Aviation Academy, Huludao Liaoning

Received: Apr. 4th, 2017; accepted: Apr. 25th, 2017; published: Apr. 28th, 2017

ABSTRACT
For the defects of pseudospectral method in solving discontinuous and non-smooth optimal control problems, a pesudospectral mesh refinement algorithm based on density function was proposed. The continuous-time optimal control problem was converted into nonlinear programming problems by using Radau pesudospectral method. The midpoints of adjacent collocation points were used as sample points, and the residuals of the dynamics constraints at these points were used as the assessment of approximation solution. The intervals where solution needs to be improved were divided into new subintervals by using the properties of curvature density function and corresponding cumulative distribution function. The algorithm can capture any discontinuities and smoothness in state and control variables, and improve the accuracy of the solution in a computational efficient manner. Simulation examples demonstrated the validity of the algorithm.
Keywords:Optimal Control Problems, Radau Pseudospectral Method, Mesh Refinement, Density Function
基于密度函数的伪谱网格细化算法及应用
王丽英1,黄诘2,张刚3
1海军航空工程学院系统科学与数学研究所,山东 烟台
2海军航空工程学院青岛分院,山东 青岛
3海军航空兵学院,辽宁 葫芦岛
收稿日期:2017年4月4日;录用日期:2017年4月25日;发布日期:2017年4月28日

摘 要
本文针对伪谱方法在求解不连续或非光滑最优控制问题上的缺点,提出了一种基于密度函数的伪谱网格细化算法,即利用Radau伪谱方法将原连续时间最优控制问题转化为非线性规划问题,取相邻配点的中点作为采样点,将动态约束在采样点上的残差作为近似解的误差评估准则;对于不满足求解精度要求的区间,利用轨迹曲率密度函数及其累积分布函数的性质将该区间进行细化。该算法能够捕捉到状态变量和控制变量的任意不连续性和非平滑性,通过有效的计算方式改进解的精度。仿真算例验证了算法的有效性。
关键词 :最优控制问题,Radau伪谱方法,网格细化,密度函数

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,伪谱法在求解无穷光滑问题时的指数收敛速度 [1] [2] 吸引了大量学者的关注,尤其是在航空航天领域,如高超声速飞行器再入轨迹快速优化 [3] 、固体运载火箭上升段轨迹优化 [4] 、再入预测校正制导 [5] 等。伪谱方法属于传统优化方法——配点法的一种。随着对配点法的深入研究,学者们逐渐发现,解的精度不仅与节点的个数、分布形状相关,还与其配置方式有关。伪谱法虽然在节点的分布形状上比传统的局部配点法(h法)具有优势——两端密集、中间稀疏的分布特点能够避免龙格现象的发生,但其配置方式是固定的(单区间分布),不能够有效地捕捉解的不连续性和非平滑特性。这种固定的节点分布方式导致了其在求解不连续或非光滑最优控制问题时,可能会出现得不到最优解或使用高维数的插值多项式也得不到理想近似解的情况发生。针对这种情况,文献 [6] 提出了一种伪谱法节点法,通过将时间区间在不连续点或奇点处划分为多个小块,在每个区间内采用全局插值多项式近似函数,但对于大多数最优控制问题来说,不连续点和奇点的个数及位置是不可能提前获知的。因此,有必要对伪谱网格细化算法进行研究。
目前,关于网格细化算法的研究主要集中在h法上,大量的学者对静态网格细化算法和动态网格细化算法进行了深入研究。文献 [7] 针对多目标优化提出了一种基于代理模型的自适应网格细化算法;文献 [8] 针对再入飞行器提出了一种基于自适应可变伪谱插值法的在线轨迹优化算法。文献 [9] [10] 提出了一种基于节点密度函数的网格细化算法,虽然避免了传统h法的等间距节点分布方式,一定程度上提高了近似解的精度和计算效率,但达不到伪谱方法的收敛速度。
本文将密度函数引入伪谱方法中,提出了一种基于密度函数的伪谱网格细化算法。利用轨迹曲率在一定程度上反映了解的平滑性的特点,基于轨迹曲率密度函数及其累积分布函数的性质来捕捉解的不连续性和非光滑性,定义新增区间网点的位置,将区间做进一步细化,利用Radau伪谱法将多区间非线性最优控制问题转化为非线性规划问题,采用SNOPT求解。
2. 多区间连续时间最优控制问题的一般性描述
传统的单区间连续时间最优控制问题是指,定义状态变量和控制变量,使如式(1)所示的Bolza型代价函数在满足各种约束的条件下达到最小化
 (1)
(1)
约束条件
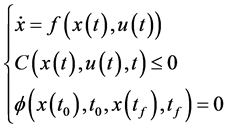 (2)
(2)
式中,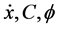 分别表示动态约束、路径约束、边界约束;
分别表示动态约束、路径约束、边界约束; 表示Mayer型代价函数,
表示Mayer型代价函数, 表示Lagrange型代价函数。
表示Lagrange型代价函数。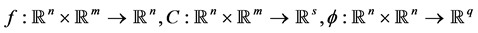 。
。
多区间非线性最优控制问题是指将问题(1)~(2)的时间区间划分为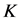 个网格子区间
个网格子区间 。令
。令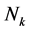 表示第
表示第 个子区间内的配点,
个子区间内的配点, 表示
表示 个网点。
个网点。
首先,通过如式(3)所示的时域转换关系,将每个网格子区间的时域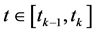 转变为
转变为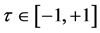
 (3)
(3)
逆转换形式为 ,于是
,于是 。
。
接着,进一步利用式(4)将网点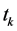 表示为初始时间
表示为初始时间 ,末端时间
,末端时间 和常数
和常数 的函数
的函数
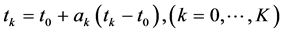 (4)
(4)
其中,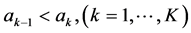 且
且 。
。
注1:通过式(4)的变换后,可将由式(1)~(2)所描述的单区间最优控制问题转化为由式(5)~(6)所描述的多区间最优控制问题。即最小化多区间Bolza型代价函数
 (5)
(5)
满足约束条件
 (6)
(6)
注2:对于由式(5)~(6)所描述的多区间最优控制问题,在每个区间内采用Radau伪谱方法将其转化为相应的非线性规划问题。
3. 伪谱网格细化算法
实施网格细化策略的第一步是要确定解的某种误差评估准则,然后根据这一准则判断需要进一步改进求解精度的区间,并在该区间实施网格细化策略。伪谱方法在离散化过程中是采用Lagrange插值多项式作为基函数来近似状态变量和控制变量的,其优点在于插值点上函数的近似值与实际值相等。因此,在优化求解过程中,若能得到原连续时间最优控制问题的确切解,则动态约束方程应该在配点间的任意点上得到满足。
本文将动态约束方程在配点间的被满足程度作为解的误差判定准则。下面,以第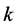 个网格子区间
个网格子区间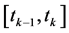 为例,对伪谱法网格细化算法的流程加以说明。
为例,对伪谱法网格细化算法的流程加以说明。
3.1. 解的误差判定准则
令 (Lagrange多项式的维数)表示区间的配点数,取相邻配点的中点
(Lagrange多项式的维数)表示区间的配点数,取相邻配点的中点 作为采样点。将动态约束方程在采样点上的残差作为解的误差评估准则,如式(7)所示:
作为采样点。将动态约束方程在采样点上的残差作为解的误差评估准则,如式(7)所示:
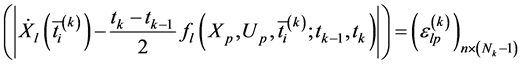 (7)
(7)
设 为给定的误差门限值。当式(7)中的每个元素都比小时,认为满足求解精度要求;否则,将该区间做进一步的细化,以改进求解精度。
为给定的误差门限值。当式(7)中的每个元素都比小时,认为满足求解精度要求;否则,将该区间做进一步的细化,以改进求解精度。
3.2. 基于曲率密度函数的细化策略
3.2.1. 密度函数的定义
若函数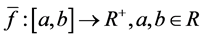 为一个非负Lebesgue可积函数,且满足
为一个非负Lebesgue可积函数,且满足 ,则称
,则称 为密度函数。与其对应的累积分布函数
为密度函数。与其对应的累积分布函数 可表示为
可表示为 。任意给定的的非负函数
。任意给定的的非负函数 都可以通过式(8)转化为密度函数
都可以通过式(8)转化为密度函数
 (8)
(8)
根据密度函数及其累积分布函数的性质可知: 若在区间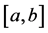 内插入
内插入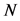 个点
个点 ,其中,
,其中,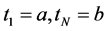 ,则如果知道第
,则如果知道第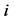 个点
个点 的位置,那么第
的位置,那么第 个点
个点 的位置可由式(9)确定
的位置可由式(9)确定
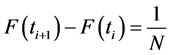 (9)
(9)
文献 [9] 指出,基于曲率的密度函数能够生成所求函数曲线的最佳分段线性近似。同时,曲线的曲率在一定程度上还反映了曲线的平滑性。因此,以下选取经过插值后得到的状态轨迹的曲率函数作为进一步细化区间所需的密度函数,通过轨迹曲率密度函数所对应的累积分布函数确定新增加网点的位置。
3.2.2. 新增区间位置的确定
设 表示第
表示第 个子区间内,优化得到的离散状态变量经过lagrange插值后得到的状态轨迹,则轨迹曲率函数定义如下:
个子区间内,优化得到的离散状态变量经过lagrange插值后得到的状态轨迹,则轨迹曲率函数定义如下:
 (10)
(10)
则由式(10)所定义的曲率函数而构成的密度函数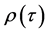 可表示为
可表示为 ,其中
,其中 为一选定的常数,满足
为一选定的常数,满足 。于是,与其对应的累积分布函数为
。于是,与其对应的累积分布函数为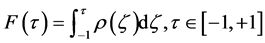 。
。
参考式(9),通过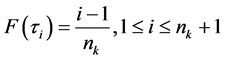 确定新增网点的位置,其中,
确定新增网点的位置,其中, 可取大于1的任意整数。本章算例中取
可取大于1的任意整数。本章算例中取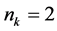 ,对于新增加的子区间,同样使用
,对于新增加的子区间,同样使用 维的插值多项式来近似状态变量和控制变量。
维的插值多项式来近似状态变量和控制变量。
3.3. 算法流程
注3:图1中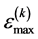 表示
表示 中的最大值,且在算法实施过程中,若
中的最大值,且在算法实施过程中,若 ,则
,则 取值应偏大;若
取值应偏大;若 ,则
,则 取值应偏小。注4。由算法流程可以看出该算法属于一种偏h的伪谱细化过程,为叙述方便用自适应h伪谱法代替伪谱网格细化。
取值应偏小。注4。由算法流程可以看出该算法属于一种偏h的伪谱细化过程,为叙述方便用自适应h伪谱法代替伪谱网格细化。
4. 验证算例
下面,以月球着陆的轨迹优化问题 [11] 为例,对自适应h伪谱法和自适应p伪谱法的优化性能进行比较分析。
最小化代价函数

满足如下的动态约束、边界条件和控制路径约束

优化结束时自适应h伪谱法和自适应p伪谱法优化策略的节点分布方式如图2所示,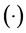 表示程序初始化时对应的子区间个数和每个区间内的配点数。
表示程序初始化时对应的子区间个数和每个区间内的配点数。
图3为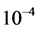 精度要求下,采用两种算法在求解上述最优控制问题优化结束时的控制变量和状态变量随时间的变化曲线。结合三图可知:(1) 自适应p伪谱法的节点分布保持两端密集、中间稀疏的特点;而自适应h-Radau伪谱法的节点分布不具备这一特点,它将时间区间进行了划分,图中靠近的三个点属于同一个子区间;(2) 在控制变量表现出不连续性、控制变量表现出非光滑性的位置附近,自适应h伪谱法节点分布比较密集。
精度要求下,采用两种算法在求解上述最优控制问题优化结束时的控制变量和状态变量随时间的变化曲线。结合三图可知:(1) 自适应p伪谱法的节点分布保持两端密集、中间稀疏的特点;而自适应h-Radau伪谱法的节点分布不具备这一特点,它将时间区间进行了划分,图中靠近的三个点属于同一个子区间;(2) 在控制变量表现出不连续性、控制变量表现出非光滑性的位置附近,自适应h伪谱法节点分布比较密集。
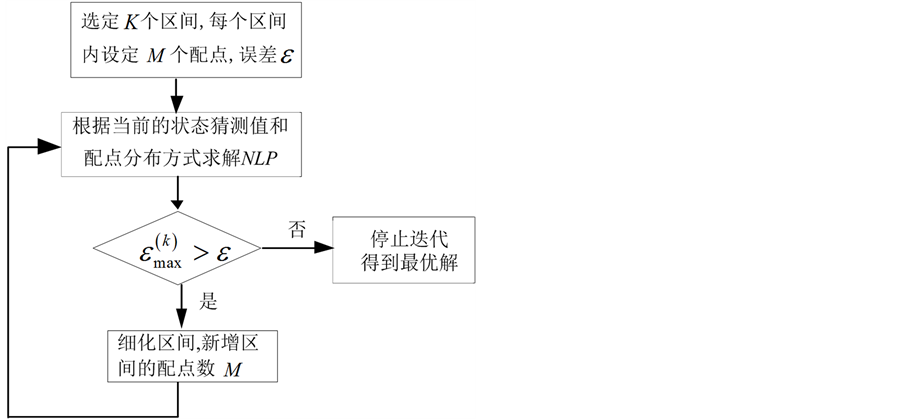
Figure 1. Algorithm flow
图1. 算法流程

Figure 2. Nodes distribution pattern of different pseudospectral methods
图2. 不同伪谱法的节点分布方式
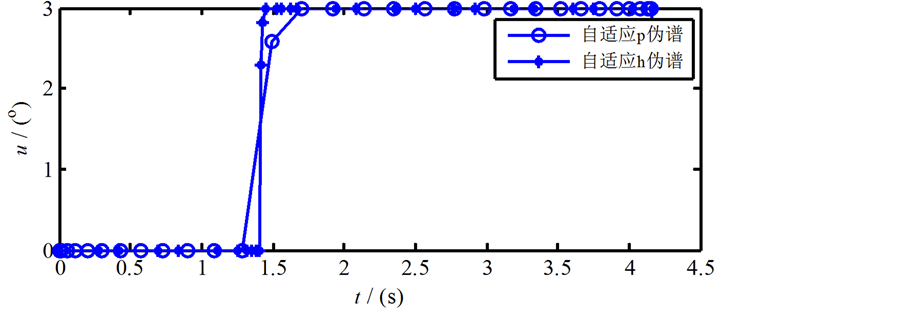

Figure 3. Control and state curves of different pseudospectral methods with times
图3. 不同伪谱法下的控制、状态变量随时间变化曲线
上述分析过程表明,对于不连续或非光滑的最优控制问题,自适应h伪谱法能够精确的捕捉状态变量和控制变量的非平滑性和不连续性,自适应p伪谱方法不具备这一特点。
表1 (Ap代表自适应p伪谱法,Ah代表自适应h伪谱法)给出了两种方法在不同精度要求下的仿真结
Table 1. Comparision of optimization result of difference accuracy
表1. 不同精度下的优化结果比较
果。从优化时间、节点数、迭代次数和代价函数上对两种方法的进行了比较。分析表1可得到以下结论:(1) 两种方法均能求解相应的最优控制问题,不同精度要求下的代价函数值在8.2458~8.2498之间,相差不大;(2) 随着精度要求的提高,优化所需的节点数、优化时间及迭代次数都在增大,这符合伪谱法求解最优控制问题的特点;(3) 所有精度下,自适应h伪谱法的优化时间均小于自适应p伪谱法;随着求解精度要求的提高,自适应p伪谱方法需要双倍的计算代价才能达到自适应h伪谱法的求解精度。
整个分析过程表明,对于非光滑最优控制问题的求解,自适应h伪谱法能够较精确的捕捉状态变量和控制变量的不连续性及非平滑性,并以较少的计算代价得到较高精度的解。
5. 结论
本文针对具有不连续性或非平滑性的最优控制问题,给出了一种新的自适应伪谱离散化解法——伪谱网格细化算法,并通过设定解的误差准则,在不满足精度要求的区间引入轨迹曲率密度函数将区间细化。这一自适应过程避免了对解的不连续点和奇点的先验知识。最后通过实例验证了该算法与自适应p伪谱法相比,能够精确的捕捉解的不连续性和非平滑性,以较少的计算代价得到较高精度的解。
基金项目
山东省自然科学基金(No.ZR2014AM006)。
文章引用
王丽英,黄 诘,张 刚. 基于密度函数的伪谱网格细化算法及应用
Pseudospectral Mesh Refinement Algorithm Based on Density Function and Its Application[J]. 动力系统与控制, 2017, 06(02): 35-42. http://dx.doi.org/10.12677/DSC.2017.62005
参考文献 (References)
- 1. Gong, Q., Kang, W. and Ross, I.M. (2006) A Pseudospectral Method for the Optimal Control of Constrained Feedback Linearizable Systems. IEEE Transactions on Automatic Control, 51, 1115-1129. https://doi.org/10.1109/TAC.2006.878570
- 2. Kang, W. (2010) Rate of Convergence for the Legendre Pseudo-spectral Optimal Control of Feedback Linearizable Systems. Journal of Control Theory and Applications, 8, 391-405. https://doi.org/10.1007/s11768-010-9104-0
- 3. 雍恩米, 唐国金, 陈磊. 基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J]. 宇航学报, 2008, 29(6): 1766-1772.
- 4. Guo, X. and Zhu, M. (2013) Direct Trajectory Optimization Based on a Mapped Chebyshev Pseudospectral Method. Chinese Journal of Aeronautics, 26, 401-402. https://doi.org/10.1016/j.cja.2013.02.018
- 5. 水尊师, 周军, 葛致磊. 基于高斯伪谱方法的再入飞行器预测校正制导方法研究[J]. 宇航学报, 2011, 32(6): 1249-1255.
- 6. Ross, I.M. and Fahroo, F. (2004) Pseudospectral Knotting Methods for Solving Optimal Control Problems. Journal of Guidance, Control, and Dynamics, 27, 397-405. https://doi.org/10.2514/1.3426
- 7. Chowdhury, S. and Mehmani, A. (2016) Adaptive Model Refinement in Surrogate-Based Multiobjective Optimization. 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Mate-rials Conference, San Diego, 4-8 January 2016, AIAA 2016-0417. https://doi.org/10.2514/6.2016-0417
- 8. Sa-gliano, M., Mooij, E. and Theil, S. (2016) Onboard Trajectory Generation for Entry Vehicles via Adaptive Multivariate Pseudospectral Interpolation. AIAA Guidance, Navigation, and Control Conference, San Diego, 4 January 2016, AIAA 2016-2115. https://doi.org/10.2514/6.2016-2115
- 9. Zhao Y. and Tsiotras P. (2009) Mesh Refinement Using Density-Function for Solving Optimal Control Problems. Infotech and Aerospace Conference, Seattle, 6-9 April 2009, AIAA Paper 2009-2019. https://doi.org/10.2514/6.2009-2019
- 10. Zhao Y. and Tsiotras P. (2011) Density Functions for Mesh Refinement in Numerical Optimal Control. Journal of Guidance, Control, and Dynamics, 34, 271-277. https://doi.org/10.2514/1.45852
- 11. Betts, J.T. (1998) Survey of Numerical Methods for Trajectory Optimization. Journal of Guidance, Control, and Dynamics, 21, 193-207. https://doi.org/10.2514/2.4231
