Dynamical Systems and Control
Vol.
11
No.
04
(
2022
), Article ID:
56872
,
9
pages
10.12677/DSC.2022.114017
含有动态参数不确定性的混合时滞复杂网络的完全同步
雷赫珊,贾 诺
哈尔滨师范大学,黑龙江 哈尔滨
收稿日期:2022年9月18日;录用日期:2022年10月8日;发布日期:2022年10月19日

摘要
本文研究了动态参数不确定性的复杂网络在混合时滞下的自适应完全同步。时变节点时滞、耦合时滞和分布时滞被添加到动态模型方程中用来研究混合时滞是如何影响网络的动态行为的。模型中动态参数的不确定性更符合实际系统并能更好地扩展其应用。应用了一个简单的自适应控制器便可处理网络之间的同步关系。最后通过数值模拟验证网络同步的可行性。
关键词
复杂网络,未知参数,混合时滞,自适应控制

Complete Synchronization of Complex Networks with Uncertain Parameters and Mixed Delays
Heshan Lei, Nuo Jia
Harbin Normal University, Harbin Heilongjiang
Received: Sep. 18th, 2022; accepted: Oct. 8th, 2022; published: Oct. 19th, 2022

ABSTRACT
In this paper, adaptive complete synchronization of complex networks with dynamic parameter uncertainties under mixed delays is investigated. Time-varying node delays, coupling delays and distributed delays are added to the dynamic model equations to study how mixed delays affect the dynamic behavior of the network. The uncertainty of dynamic parameters in the model is more consistent with the actual system and can extend its application better. A simple adaptive controller is applied to resolve the synchronization relationship between the networks. Finally, the feasibility of network synchronization is verified by numerical simulation.
Keywords:Complex Networks, Unknown Parameters, Mixed Delays, Adaptive Control

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
复杂网络技术的发展为语言研究提供了新的视角和手段 [1] ,对复杂网络的研究主要是从抽象的数学模型出发研究各种复杂网络所具有的共性以及对其加以控制利用的普遍方法 [2] 。网络中的节点构成迥异,数目众多,且节点间的耦合强度和耦合关系复杂,但大规模节点突然地一起运动或行动就会导致同步现象的出现 [3] ,因此网络同步现象在数学、医学等各种学科领域内不断被深入研究 [4] [5] [6] [7] 。时滞是网络化控制系统中时常会发生的一种不可避免的现象,针对这种现象,许多专家学者近年来提出了不同方法予以解决 [8] [9] [10] [11] 。文献 [12] 研究了一类在网络中含有服从二项分布的随机离散时滞项在带有时滞特性的脉冲控制器的影响下所产生的网络之间同步问题,在脉冲控制时滞下通过Lyapunov稳定性理论解决了网络中带有随机时变时滞这类特殊情形的同步问题。文献 [13] 研究了几类网络的外同步问题。针对普通复杂网络以及在复数域下的同步问题,给出了一个较为复杂的控制器,其控制器是非线性与自适应相互结合的一类混合设计,能用来更好地解决带有时滞和随机扰动的复杂网络或神经网络之间的同步问题。文献 [14] 研究了两个带有不确定参数、结构以及干扰的网络之间的同步问题。分别讨论了参数确定以及不确定、结构相同以及不同时下的两个网络之间的同步问题,给出了多种讨论方案用以验证网络之间在干扰下的同步问题,具有更好的现实性。因此基于网络中的多种情况,我们在下文中给出了带有未知参数以及混合时滞的一类复杂网络,来探究其同步问题。
2. 初步介绍和模型描述
根据网络动力学理论,网络中每个节点的行为或状态可以用一个动态方程
来描述。本文中我们考虑同时具有节点时滞、耦合时滞和分布时滞的耦合复杂网络,并将此网络作为驱动网络,其节点状态方程描述为:
(1)
式子中
表示第i个节点在t时刻的状态向量,其中
。向量函数
是驱动网络带有未知参数的动态方程,保证连续可微,满足
。
, 是驱动网络中的内部耦合矩阵。向量函数
是非线性光滑函数,同样满足连续且可微,表示网络的动态特性。
为节点的时变时滞,
为系统的耦合时滞以及
为系统的分布时滞。具有时滞的外部耦合矩阵
, 描述网络的拓扑结构,并且要求满足下面条件:如果节点i和j存在时滞耦合(
),那么
, 否则有
。此外矩阵L,D均需要满足耗散耦合条件(2):
(2)
在这里为了方便探究,我们默认耦合强度为1。基于混沌同步的驱动–响应概念,我们给出对应网络(1)的响应网络模型:
(3)
其中
为第i个节点的状态向量,
为响应网络节点的动态函数并且同样满足
。响应模型(3)中的
是响应系统中仍需要设计的控制器,并且有
。根据驱动–响应系统之间节点的状态误差向量来不断调整响应网络的节点的状态。其余表示方法均与式(1)表示相同,这里不再赘述。从本文的模型构建中可以看出,我们的模型考虑了混合时滞的影响,并且动态参数
是未知的,这样的网络模型能更好的反映出一般性。
接下来我们给出两个网络之间的节点状态误差向量,表示为:
, (4)
这里
。当网络(1)与网络(3)实现完全同步时,每个节点的状态误差向量需要满足以下条件:
, (5)
式(3)中的控制器
可以根据耦合结构和节点动态参数的变化而更新其参数。自适应控制器可视为是一种在线参数估计器与由参数已知时得出的控制律的一种组合。这种组合方法加上估计器和控制律的类型就提出了各种不同性质、不同类型的自适应控制器 [15] 。因此自适应控制器被重点应用于解决网络之间的同步问题。为了更好的研究问题,我们给出以下假设和引理:
假设1:
是连续可微的,并且满足
,。其中
假设2:
, 都是连续有界函数,对于任意向量
,存在正常数
满足
引理1 [16] :对于任意的
为n维实数矩阵,
为合适的正常数,则有
引理2 [17] :对于耦合矩阵
有
1)
且
,其中
,
2) 若矩阵L符合上述条件并且为不可约的,则通过L所求的任何一个非零特征值的实部均为负数。
3) 存在一个矩阵
,使得
成立,这里
是L的所有特征值。
这里的耦合矩阵D均有类似性质。
引理3 [18] :对于任意正定对称矩阵W,标度常量a和b (
),向量函数
有
成立。
3. 主要结论
节点动态参数
是具有未知参数的,因此在这种情况下我们可以把
分裂成为以下形式:
(6)
其中A和f是节点状态向量的两个函数,
是未知参数的向量,m是未知参数的个数。网络之间相应的节点状态误差向量的变化率表示为:
将网络(1)与(3)带入后可得到
(7)
其中有:
定理1:当网络中含有未知参数的动态函数存在时,驱动网络和响应网络可以取如下控制器实现网络之间的完全同步:
(8)
其中
,满足
为任意正常数。
是t时刻
的估计,并且
。从而得到网络之间相应节点状态误差向量的变化率为
(9)
证明:选取如下Lyapunov函数:
其中
(10)
这里
是一个不确定的非负数。对上述Lyapunov函数进行求导可得到
应用上述引理以及假设可得
同理可得到
上式
中,当
时,
;当
,。
将上述式子整理到一起得到
(11)
这里
。选取合适的值
以及
时,保证了Lyapunov函数为负定。根据Barbalat引理 [19] 可知,状态向量的极限误差值趋近于0,也就是说有
。因此在我们所设计的自适应控制器下,驱动网络与响应网络之间可以达到完全同步,并且其同步是全局稳定的。
4. 数值模拟
不失一般性,本章我们选取了一个具有四个节点的复杂网络,其驱动系统如下:
其中
是具有未知参数的并且有
,因而我们在数值模拟中设定其为
,,。这里
作为未知参数的向量估计,
其中标量值
,,,。参数设置保证了两个系统是混沌的并且有
,,
为了便于研究,我们选择了耦合时滞
。对应的响应系统为
类似的有
,。控制器中
。我们得到误差系统如下
仿真结果显示:驱动系统(1)与响应系统(3)的运动轨迹如下图1,图2所示。不受控制的误差系统的运动轨迹如图3所示。此外图4显示出了在我们所设计的控制器下,驱动系统与响应系统可以在一定时间内完成同步,因此可以反映出我们的理论结果是有效的。
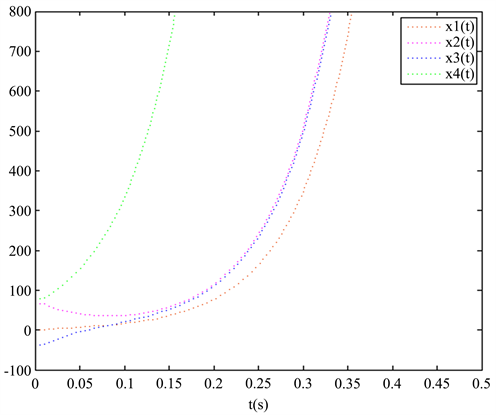
Figure 1. The trajectories of drive system
图1. 驱动系统的运动轨迹
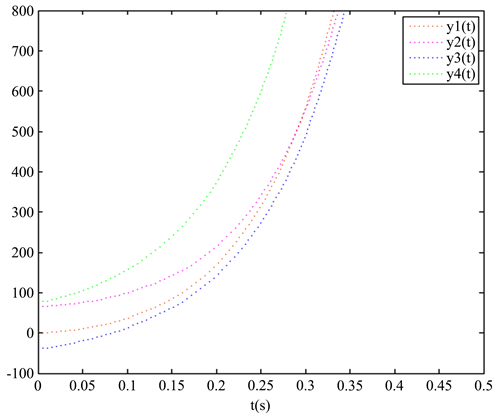
Figure 2. The trajectories of response system
图2. 响应系统的运动轨迹
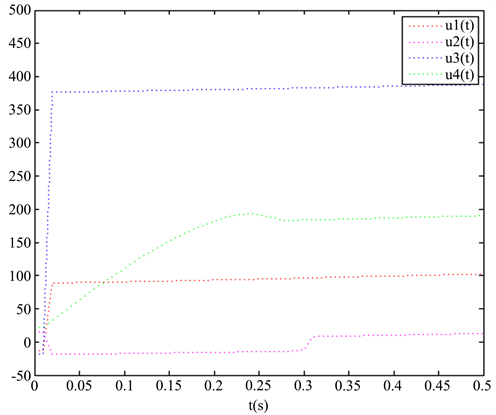
Figure 3. The trajectories of error system without controller
图3. 无控制器作用的误差系统轨迹

Figure 4. The trajectories of error system under controller
图4. 有控制器作用的误差系统轨迹
5. 结论
本文我们研究了一类带有动态参数不确定性的混合时滞复杂网络。通过设计一种适应模型本身的自适应控制器通过对混合时滞以及未知参数不确定的针对性处理,有效且简单的解决了网络之间的同步问题,并且通过数值模拟也有效地验证了文章的合理性。因此自适应控制器是解决网络之间完全同步的一种重要方法,正在被广泛使用。因此我们将应用自适应方法去解决未来更多的网络中的问题。
文章引用
雷赫珊,贾 诺. 含有动态参数不确定性的混合时滞复杂网络的完全同步
Complete Synchronization of Complex Networks with Uncertain Parameters and Mixed Delays[J]. 动力系统与控制, 2022, 11(04): 151-159. https://doi.org/10.12677/DSC.2022.114017
参考文献
- 1. 赵怿怡, 刘海涛. 语言网络研究的数学模型——从复杂网络、社会网络到语言网络[J]. 中文信息学报, 2015, 29(6): 46-53.
- 2. 贾兴, 孙海义. 复杂网络同步控制研究方法综述[J]. 动力系统与控制, 2018, 7(4): 318-327.
https://doi.org/10.12677/DSC.2018.74036
- 3. 杨彦清. 时变耦合复杂网络同步的自适应控制[J]. 微计算机信息, 2010, 26(4): 205-206.
- 4. 毛北行, 李巧利. 复杂网络同步时间可控的投影同步[J]. 安徽大学学报(自然科学版), 2019, 39(2): 13-16.
- 5. 张峥, 朱炫颖. 复杂网络同步控制的研究进展[J]. 信息与控制, 2017, 46(1): 103-112.
- 6. 李帆, 程云章, 边俊杰, 耿晓斌. 基于PPG信号LSTM网络同步动脉血压预测[J]. 软件导刊, 2020, 19(8): 44-48.
- 7. Atiyeh, B., Sajad, J. and Hamed, A. (2022) Explosive Synchronization: From Synthetic to Real-World Networks. Chinese Physics B, 31, Article ID: 020504.
https://doi.org/10.1088/1674-1056/ac3cb0
- 8. 郑晓军, 谭平, 姚洪灿. 基于遗传算法优化的Elman网络时滞补偿研究[J]. 广州建筑, 2022, 50(1): 3-10.
- 9. 张伟, 佟绍成. 基于事件触发的模糊网络时滞系统的容错控制[J]. 模糊系统与数学, 2019, 33(3): 19-28.
- 10. 王宇娟, 涂俐兰, 宋帅, 李宽洋. 耦合含时滞的相互依存网络的局部自适应异质同步[J]. 物理学报, 2018, 67(5): 60-70.
- 11. 梁义, 王兴元. 结点含时滞的具有零和非零时滞耦合的复杂网络混沌同步[J]. 物理学报, 2013, 62(1): 516-521.
- 12. 杨尚霖, 杨宇璐, 陈珂熙. 随机时滞复杂网络的脉冲滞后同步[J]. 中国科技信息, 2018(17): 70-73.
- 13. 张雅美. 几类时滞复杂网络的外同步控制研究[D]: [硕士学位论文]. 大连: 大连理工大学, 2016.
- 14. Wang, G., Lu, S.W., Liu, W.B., and Ma, R.N. (2022) Adaptive Complete Synchronization of Two Complex Networks with Uncertain Parameters, Structures and Disturbances. Journal of Computational Science, 54, Article ID: 101436.
- 15. 赵英, 刘鹏, 刘荣. 自适应控制器概述[J]. 中国集体经济, 2008(6): 157-158.
- 16. Zhao, C.D., He, P., Nik, H.S. and Ren, J.C. (2015) Robust Adaptive Synchronization of Uncertain Complex Networks with Multiple Time-Varying Coupled Delays. Complexity, 20, 62-73.
https://doi.org/10.1002/cplx.21531
- 17. 张川. 复杂网络的若干控制同步问题研究[D]: [博士学位论文]. 大连: 大连理工大学, 2018.
- 18. Zheng, C.D., Qi, H.S. and Wei, Z.P. (2018) Stochastic Synchronization for an Array of Hybrid Neural Networks with Random Coupling Strengths and Unbounded Distributed Delays. Neurocomputing, 273, 22-36.
https://doi.org/10.1016/j.neucom.2017.07.062
- 19. 孟晓玲, 毛北行. 含对数阶分数阶T混沌系统的滑膜同步[J]. 山东大学学报(工学版), 2020, 50(5): 7-12.









