Hans Journal of Civil Engineering
Vol.05 No.05(2016), Article ID:18355,10
pages
10.12677/HJCE.2016.55023
Study on the Constitutive Model of Rock Damage Based on Intermediate Principal Stress Criterion
Siqi Liu, Yonglai Zheng, Shuxin Deng
College of Civil Engineering, Tongji University, Shanghai

Received: Aug. 1st, 2016; accepted: Aug. 19th, 2016; published: Aug. 22nd, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
By discussing the form of new rock micro-unit strength based on intermediate principal stress criterion, which satisfies Weibull random distribution, and introducing a damage correction factor q, a statistical constitutive model of rock damage was developed based on the stress-strain curve of tri-axial tests for rocks. Moreover, the effect of the parameters of Weibull distribution and the damage correction factor on the model was studied. The model was rectified according to the properties of tri-axial stress-strain test curve of rock. Compared with the existing research results, this model can better simulate the rock strain softening under low confining pressure. Therefore, this model has broad prospects for application.
Keywords:Rock Failure, Damage, Intermediate Principal Stress, Constitutive Model

基于中主应力强度准则岩石损伤本构模型研究
刘斯奇,郑永来,邓树新
同济大学土木工程学院,上海

收稿日期:2016年8月1日;录用日期:2016年8月19日;发布日期:2016年8月22日

摘 要
从探讨基于中主应力效应的新的岩石微元强度表示方法及其服从Weibull随机分布的特点出发,并引入损伤修正系数 ,基于岩石三轴应力应变试验曲线,建立了岩石损伤统计本构模型。在此基础上,重点研究了Weibull分布参数以及损伤修正系数对岩石损伤本构统计模型的影响,并结合岩石三轴应力应变试验曲线的特点,对岩石损伤本构统计本构模型进行了合理修正。与试验结果及前人研究结果比较,该模型可以更好地模拟岩石在低围压下应变软化的情况,具有广阔的应用前景。
,基于岩石三轴应力应变试验曲线,建立了岩石损伤统计本构模型。在此基础上,重点研究了Weibull分布参数以及损伤修正系数对岩石损伤本构统计模型的影响,并结合岩石三轴应力应变试验曲线的特点,对岩石损伤本构统计本构模型进行了合理修正。与试验结果及前人研究结果比较,该模型可以更好地模拟岩石在低围压下应变软化的情况,具有广阔的应用前景。
关键词 :岩石破裂,损伤,中主应力,本构模型

1. 引言
天然岩石由于成岩作用和成岩环境的不同导致其内部往往含有大量的孔隙、裂隙等缺陷,这些缺陷一般分布在整个岩石材料之中。在外部荷载作用下,材料的细观结构中可以发生缺陷的形核、长大等不可逆的热力学耗散过程,在宏观上通常表现为材料力学性能的裂化直至破坏,而这种过程称为材料的损伤 [1] 。针对这些损伤,学者们提出了各种损伤模型 [2] - [6] 。
纵观现有强度模型研究,最常用的是Mohr-Coulomb准则和Drucker-Prager准则,前者因没有考虑中主应力的影响,计算结果偏于保守,而后者视中主应力与最小主应力对强度的影响一样,计算结果而又偏于危险 [7] [8] 。因此,本文建立了基于中主应力强度准则的岩石微元强度表示方法。同时引入损伤修正系数q,来反映岩石的非均匀性、非线性特征。考虑岩石微元强度服从Weibull分布的特点,建立了模拟岩石破裂全过程的损伤统计本构模型,并在此基础上,重点探讨了本构模型参数与围压的关系,并对模型进行相应的修正。通过试验及前人研究结果验证了模型的正确性,该研究具有重要的理论与实用意义。
2. 岩石损伤本构模型的建立
2.1. 基本假设
岩石材料内部构造的极不均质,含有不同程度的缺陷,各微元强度也就不相同,为了方便分析,做以下假设:
1) 在宏观上,微元体及其损伤均表现为各向同性;
2) 在微元破坏前服从虎克定律,即微元体具有线弹性性质,破坏后不具备承载能力;
3) 各微元弹性体的强度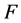 服从概率统计规律。本文选用Weibull分布来描述各微元体强度
服从概率统计规律。本文选用Weibull分布来描述各微元体强度 的分布规律,其概率密度函数为:
的分布规律,其概率密度函数为:
 (1)
(1)
式中:F为微元强度随机分布的分布变量;m和F0为Weibull分布参数。
2.2. 岩石损伤本构关系
根据Lemaitre教授提出的应变等效原理 [9] ,即损伤材料在有效应力作用下产生的应变与同种材料无损时发生的应变等价。根据这一原理,用损伤后的有效应力替换无损材料本构关系中的名义应力,就可以推导出受损材料的任何应变本构关系。在此基础上,建立如下的岩石损伤本构关系式为 [9]
 (2)
(2)
式中: 为材料的弹性矩阵,
为材料的弹性矩阵,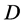 为损伤变量,
为损伤变量, 为名义应力矩阵,
为名义应力矩阵,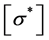 为有效应力矩阵,
为有效应力矩阵,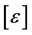 为应变矩阵。
为应变矩阵。
在三维情况下的损伤变量为一个代表性体积单元内损伤的等效面积与该截面总面积的比值 [10] 。当此比值不受截面的方位影响时,就是各向同性损伤,即各个方向的损伤变量都为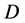 。但多数岩石类材料并非如此,岩石存在初始孔隙,同时破裂后的岩石还存在剩余强度。按照以上假设的Weibull分布是不能反映岩石的剩余强度特征的。损伤力学最初是为了分析受拉金属损伤现象引入有效应力的,假设通过损伤不能传播力。然而在岩石受压过程中,岩石微元破坏后还可以传递部分压应力和剪应力。考虑以上因素,本文沿用文献 [11] 的方法,引入损伤修正系数
。但多数岩石类材料并非如此,岩石存在初始孔隙,同时破裂后的岩石还存在剩余强度。按照以上假设的Weibull分布是不能反映岩石的剩余强度特征的。损伤力学最初是为了分析受拉金属损伤现象引入有效应力的,假设通过损伤不能传播力。然而在岩石受压过程中,岩石微元破坏后还可以传递部分压应力和剪应力。考虑以上因素,本文沿用文献 [11] 的方法,引入损伤修正系数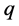 ,
,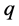 为从0到1变化的系数。系数
为从0到1变化的系数。系数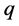 在一定程度上表征了岩石材料的不均匀性、各向异性和初始孔隙的存在,即反映了岩石的非均匀性、非线性特征。
在一定程度上表征了岩石材料的不均匀性、各向异性和初始孔隙的存在,即反映了岩石的非均匀性、非线性特征。
按照损伤变量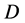 的定义及引入的初始损伤系数
的定义及引入的初始损伤系数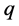 ,将式(2)修正为如下岩石损伤的本构关系:
,将式(2)修正为如下岩石损伤的本构关系:
 (3)
(3)
2.3. 统计损伤演化方程
应力随应变的变化实质上是一个材料内部损伤不断累积直至材料破坏的过程。损伤的演化发展使得本构关系呈现出非线性。岩石材料的损伤是由微元体的不断破坏引起的,设在某一级荷载作用下已破坏的微元体数目为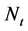 ,定义统计损伤变量为
,定义统计损伤变量为 为岩石中已经破坏的微元数目与总微元数目
为岩石中已经破坏的微元数目与总微元数目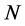 之比 [12] ,即:
之比 [12] ,即:
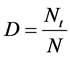 (4)
(4)
岩石内部微元的破坏在不同荷载作用下是随机的,因此岩石微元破坏的概率与其应力应变状态密切相关。为了充分反映岩石微元强度随应力状态而变化的特点,应将一个与岩石的应力应变有关的量作为去分布变量。
定义损伤变量为:
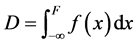 (5)
(5)
式中: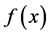 为Weibull概率密度函数。
为Weibull概率密度函数。
在任意区间 内已经破坏的微元数目为
内已经破坏的微元数目为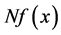 ,当加载到某一水平
,当加载到某一水平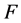 时,已经破坏的微元体数目
时,已经破坏的微元体数目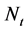 可以表示为:
可以表示为:
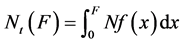 (6)
(6)
将(5)和式(1)代入到式(4)中,得到损伤变量为:
 (7)
(7)
式(7)为岩石材料在受荷载时的统计损伤演化方程。
2.4. 岩石微元强度的表征
如何确定表示式(7)中的分布变量 是推导上述演化方程的一个重要问题。文献 [13] 采用单轴应变作为分布变量,虽然取得了较好的效果,但它存在以下几个方面的问题:首先,微元破坏分布无法通过岩石单轴应变来反映;其次,岩石损伤受单轴应变和其应力应变状态的双重影响;再者,岩石损伤软化的三维本构关系无法通过由单轴应变得到的损伤本构方程全面描绘。为此,曹文贵等 [14] [15] 提出基于岩石破坏准则的岩石微元强度的表征方法,其合理性得到大大改善。文献 [11] [14] - [17] 关于岩石损伤本构模型的推导均采用了以岩石破坏准则作为微元强度度量的方法。
是推导上述演化方程的一个重要问题。文献 [13] 采用单轴应变作为分布变量,虽然取得了较好的效果,但它存在以下几个方面的问题:首先,微元破坏分布无法通过岩石单轴应变来反映;其次,岩石损伤受单轴应变和其应力应变状态的双重影响;再者,岩石损伤软化的三维本构关系无法通过由单轴应变得到的损伤本构方程全面描绘。为此,曹文贵等 [14] [15] 提出基于岩石破坏准则的岩石微元强度的表征方法,其合理性得到大大改善。文献 [11] [14] - [17] 关于岩石损伤本构模型的推导均采用了以岩石破坏准则作为微元强度度量的方法。
Mohr-Coulomb准则没有考虑强度的中主应力效应,而Drucker-Prager准则则高估了强度的中主应力效应,因此本文引用ZHENG Y等 [18] 提出的能更准确反映中主应力效应的强度准则,采用该强度准则来表征微元体的强度。岩石微元强度表示为:
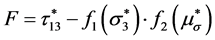 (8)
(8)
式中:
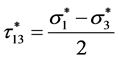 (9)
(9)
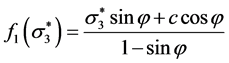 (10)
(10)
 (11)
(11)
 (12)
(12)
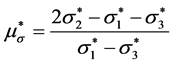 (13)
(13)
根据前文假设,由虎克定律及式(3)可以得到:
 (14)
(14)
 (15)
(15)
则用名义应力表示的岩石微元强度可表示为:
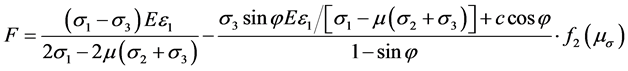 (16)
(16)
式中: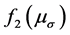 的表达式和式(11)一样,只需将Lode参数
的表达式和式(11)一样,只需将Lode参数 换成
换成 即可。
即可。
2.5. 本构关系的确立
将式(7)代入式(15),再代入式(14),得到岩石损伤统计本构模型为:
 (17)
(17)
3. 模型参数的确定
在本文建立的损伤统计本构模型的求解过程中,需要确定8个参数:两个弹性模量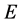 和
和 ,三个强度准则参数
,三个强度准则参数 、
、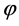 和
和 ,Weibull分布参数
,Weibull分布参数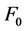 和
和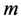 ,损伤修正系数
,损伤修正系数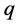 。
。 和
和 可以根据岩石的应力应变曲线的初始上升斜率来获得,表示材料未损伤时的初始弹性模量。三个强度准则参数
可以根据岩石的应力应变曲线的初始上升斜率来获得,表示材料未损伤时的初始弹性模量。三个强度准则参数 、
、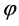 和
和 可以通过拟合岩石材料在三轴压缩条件下的强度包络线获得。下面介绍Weibull分布参数
可以通过拟合岩石材料在三轴压缩条件下的强度包络线获得。下面介绍Weibull分布参数 和
和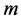 的确定方法。
的确定方法。
文献 [11] [14] [15] 采用作图法和线性回归来求解,这种方法过程过于复杂,而且需要依赖大量的试验数据,在数据不足时容易引起较大的误差。所以本文采用文献 [17] 建议的利用多元函数极值理论来求解。
如图1所示为典型的岩石三轴压缩应力应变曲线,在曲线的应力峰值点处斜率应为零:
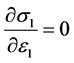 (18)
(18)
由式(17),峰值应力点还应该满足:
 (19)
(19)
对式(17)求偏微分有:
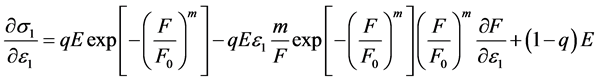 (20)
(20)
由式(7)和式(18),式(20)可变为:
 (21)
(21)
式中:
 (22)
(22)
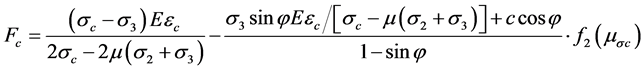 (23)
(23)
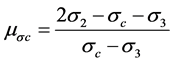 (24)
(24)
对式(16)求偏微分,并结合式(18)可得:
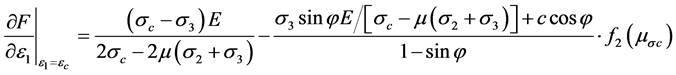 (25)
(25)
将式(25)代入式(21)可得:
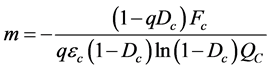 (26)
(26)
式中: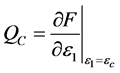 。
。
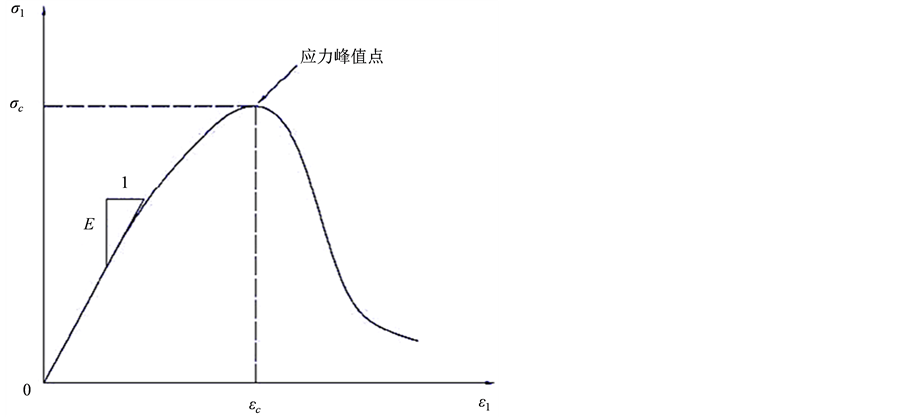
Figure 1. Stress strain curve of typical rock in three axis
图1. 典型岩石三轴压缩应力应变曲线
由式(7)得:
 (27)
(27)
下面引用文献 [19] 的试验数据资料,来进行模型拟合参数的确定。单轴压缩曲线如图2所示。通过数据处理可以得到该岩石弹性模量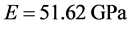 ,泊松比
,泊松比 ,内摩擦角
,内摩擦角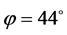 ,粘聚力
,粘聚力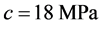 ,先设定损伤修正系数
,先设定损伤修正系数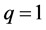 ,考虑
,考虑 情况,此时
情况,此时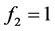 。将应力峰值点应力值
。将应力峰值点应力值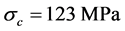 和应变值
和应变值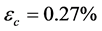 代入到式(22)和式(23)求解得到
代入到式(22)和式(23)求解得到 、
、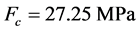 。由式(24)求解得到
。由式(24)求解得到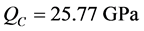 。将所得各变量代入式(27)得到
。将所得各变量代入式(27)得到 ,
, 。将参数代入式(16),再利用式(17)可计算得到应力应变曲线,在图2中用红色实线表示。由图2可知,通过上述方法确定的模型参数,计算得出曲线在峰前阶段以及应力峰值位置都和试验结果拟合得很好。
。将参数代入式(16),再利用式(17)可计算得到应力应变曲线,在图2中用红色实线表示。由图2可知,通过上述方法确定的模型参数,计算得出曲线在峰前阶段以及应力峰值位置都和试验结果拟合得很好。
4. 模型参数分析
沿用上节得到的模型参数,保持除m外的所有参数不变,将m值设定为2、3、4、5,曲线的变化如图3所示。随着m的增大,应力应变曲线的峰后软化现场越来越明显,材料的脆性增加;反之,材料的延性增大,因此参数m一定程度上反映了岩石的脆性度。m值越大,微元强度分布越集中,当材料屈服破坏时,越多的岩石微元同时破坏,所以材料将表现出更加明显的脆性特征。固定除F0外参数不变,将F0的值设定为40、50、60、70,曲线的变化如图4所示。由图4可知,当F0增大,岩石峰值应力增大,相对应的峰值应变也增大。F0反映的是岩石微元强度分布的平均值,影响岩石材料的宏观平均强度的大小,而对峰后应力跌落影响较小。固定除q外的其余参数不变,改变q的值设定为0.7、0.8、0.9、1.0,曲线的变化如图5所示。由图5可知,当q减小,岩石的应力峰值略微增大,而峰后延性增强较明显,残余强度显著增大。这说明了本文模型引入的损伤修正系数在一定程度上影响了岩石的残余强度。因此通过选择更好的修正系数值,可以更好地模拟出包括残余强度和软化特征在内的应力应变全过程曲线 [20] 。参数m、F0和q的变化对应力应变曲线的峰前线性部分没有影响,而对曲线的非线性部分的影响较为显著。

Figure 2. The curve of stress and damage variable change with strain
图2. 应力和损伤变量随应变变化曲线
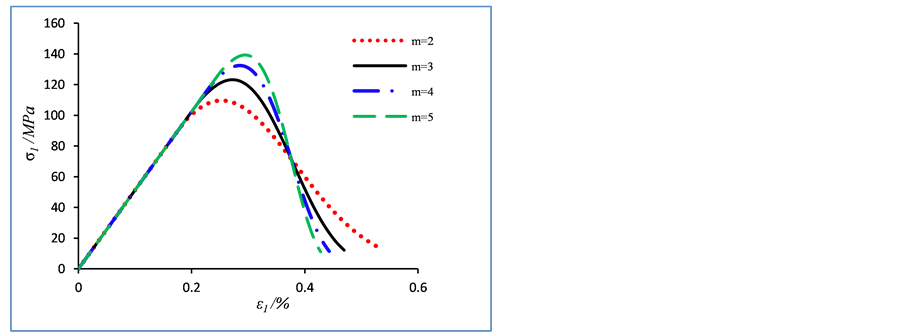
Figure 3. The influence of parameter m on the damage constitutive model of rock
图3. 参数m对岩石损伤本构模型的影响
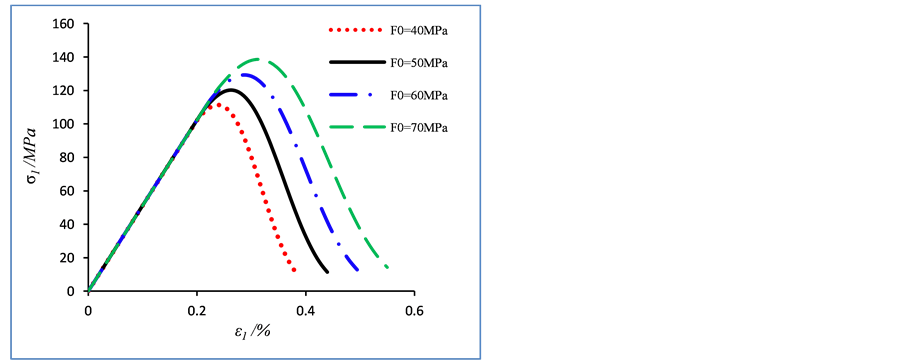
Figure 4. The influence of parameter F0 on the damage constitutive model of rock
图4. 参数F0对岩石损伤本构模型的影响
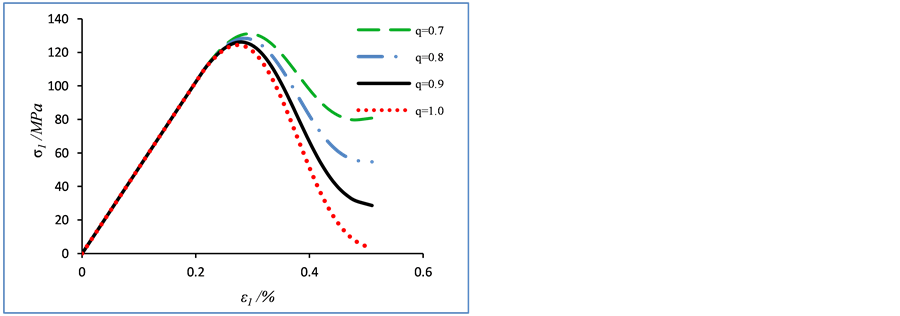
Figure 5. The influence of parameter q on the damage constitutive model of rock
图5. 参数q对岩石损伤本构模型的影响
5. 模型的验证
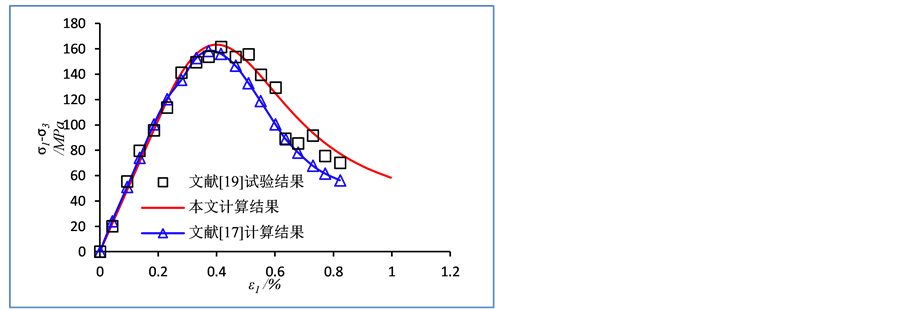
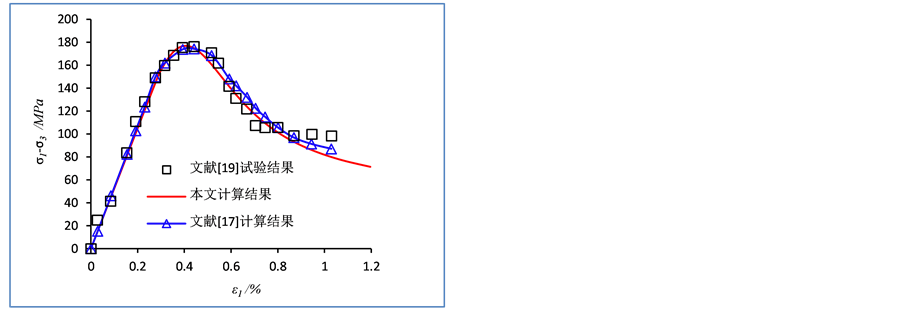
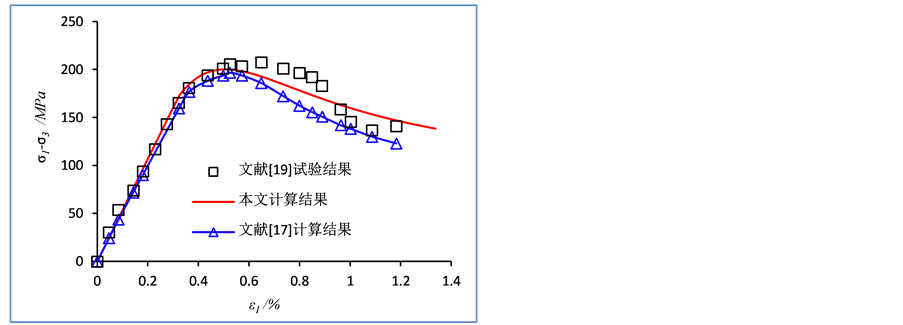
为了验证本文建立的岩石损伤统计本构模型,引用文献 [19] 的试验资料,参数的确定见3节。模型参数根据不同应力状态下残余强度和软化特征,对m、F0和q进行了调整。单轴压缩条件下的计算结果如图2所示,其余应力状态下计算结果如图6所示。本文还引入文献 [17] 的计算结果进行比较,在图2和图6中都用三角形标记表示。由图2和图6可知,本文建立的模型与试验曲线及文献 [17] 理论曲线拟合良好。在破坏前区,本文与文献 [17] 的理论曲线都和试验曲线非常一致,而在岩石破坏后的软化阶段,本文建立的模型与试验结果拟合得更好,更加符合工程实际。
图2和图7中还给出了损伤变量随应变的变化曲线。图2和图7中初始阶段模型损伤变量为零,当荷载达到一定值之后损伤突然大幅增长,而且随着围压的增大,损伤变量突然增长时刻对应的应变值增大,但是其增长的速率变缓。突然增长的应变值增大说明需要更大的应力使得材料屈服破坏,这导致材料强度的上升。损伤增长速率变缓,说明围压越大,微元体屈服破坏的速率放缓,这导致了宏观岩石材料延性的增强。
脆性岩石材料损伤的过程,可以看作是岩石内部微裂纹萌生和扩展的过程,因此在颗粒离散元数值模拟中可以用微裂纹数目的变化来表示岩石材料损伤的演化。相对于文献 [14] - [16] 中建立的模型损伤从加载的初始阶段就开始大幅增长,显然本文的模型更加合理。
6. 结语
本文将宏观方法及统计学方法相结合,基于Lemaitre应变等价原理的岩石损伤模型研究的基础上,以反映中主应力影响的强度准则作为岩石微元体强度随机分布变量,并引入损伤修正系数,建立了岩石损伤本构模型。得出的主要结论如下:
1) 所建立的模型的主要特点是能够反映三维应力状态下岩石的变形全过程,反映了岩石的破裂不仅受岩石微元强度的变化,而且受岩石应力状态的影响。采用基于破坏准则的岩石微元强度度量方法,引入反映中主应力影响的强度准则来表征岩石微元的强度,使得计算结果更加接近实际。
2) 引入损伤修正系数,使得Lemaitre应变等价性假说与损伤统计分布很好地衔接,通过调整损伤修正系数也使得本构模型的精度大为提高。
3) 与基于微裂纹变形和扩展的岩石细观损伤模型相比,本文建立的模型忽略了细观物理过程,避免了细观力学繁琐的计算,因此更容易在工程实际问题中得到应用。

(a) 围压3.5 MPa ( ) (b) 围压7.0 MPa (
) (b) 围压7.0 MPa ( )(c) 围压14.0 MPa (
)(c) 围压14.0 MPa (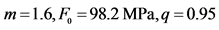 ) (d) 围压21.0 MPa (
) (d) 围压21.0 MPa ( )
)
Figure 6.The comparison between the model calculation results in this paper and the experimental results
图6. 本文模型计算结果和试验结果对比
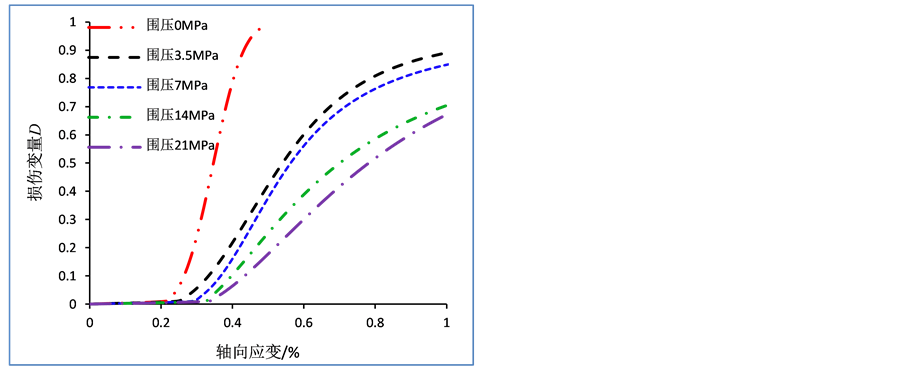
Figure 7. Rock damage evolution curve
图7. 岩石损伤演化曲线
4) 本文建立的模型参数较少,而且物理意义明确,应用方便。弹性模量参数可以通过应力应变曲线的初始段上升斜率来获得,强度准则参数可以通过拟合强度包络线来获得,Weibull分布参数可以通过多元函数极值理论来求解。
文章引用
刘斯奇,郑永来,邓树新. 基于中主应力强度准则岩石损伤本构模型研究
Study on the Constitutive Model of Rock Damage Based on Intermediate Principal Stress Criterion[J]. 土木工程, 2016, 05(05): 171-180. http://dx.doi.org/10.12677/HJCE.2016.55023
参考文献 (References)
- 1. 冯西桥, 余寿文. 准脆性材料细观损伤力学[M]. 北京: 高等教育出版社, 2002.
- 2. Kachanov, L. (2013) Introduction to Con-tinuum Damage Mechanics. Springer Science & Business Media, Berlin.
- 3. Krajcinovic, D. (2000) Damage Mechanics: Accomplishments, Trends and Needs. International Journal of Solids and Structures, 37, 267-277. http://dx.doi.org/10.1016/S0020-7683(99)00081-5
- 4. 余寿文, 冯西桥. 损伤力学[M]. 北京: 清华大学出版社, 1997.
- 5. Krajcinovic, D. (1996) Damage Mechanics. Elsevier, Amsterdam.
- 6. 谢和平. 岩石混凝土损伤力学[M]. 徐州: 中国矿业大学出版社, 1990.
- 7. 俞茂宏. 岩土类材料的统一强度理论及其应用[J]. 岩土工程学报, 1994(2): 1-10.
- 8. Ewy, R.T. (1999) Well Bore-Stability Predictions by Use of a Modified Lade Criterion. SPE Drilling and Completion, 14, 85-91. http://dx.doi.org/10.2118/56862-PA
- 9. Lemaitre, J., Sermage, J.P. and Desmorat, R. (1999) A Two Scale Damage Concept Applied to Fatigue. International Journal of Fracture, 97, 67-81. http://dx.doi.org/10.1023/A:1018641414428
- 10. 杨光松. 损伤力学与复合材料损伤[M]. 北京: 国防工业出版社, 1995.
- 11. 许金余, 范建设, 吕晓聪. 围压条件下岩石的动态力学特性[M]. 西安: 西北工业大学出版社, 2012.
- 12. Krajcinovic, D. and Silva, M.A.G. (1982) Statistical Aspects of the Continuous Damage Theory. International Journal of Solids and Structures, 18, 551-562. http://dx.doi.org/10.1016/0020-7683(82)90039-7
- 13. 唐春安. 岩石破裂过程中的灾变[M]. 北京: 煤炭工业出版社, 1993.
- 14. 曹文贵, 方祖烈. 岩石损伤软化统计本构模型之研究[J]. 岩石力学与工程学报, 1998, 17(6): 628-633.
- 15. 曹文贵, 张升. 基于Mohr-Coulomb准则的岩石损伤统计分析方法研究[J]. 湖南大学学报: 自然科学版, 2005, 32(1): 43-47.
- 16. 蒋维, 邓建, 李隐. 基于对数正态分布的岩石损伤本构模型研究[J]. 地下空间与工程学报, 2010, 6(6): 1190-1194.
- 17. 赵衡. 岩石变形特性与变形全过程统计损伤模拟方法研究[D]: [博士学位论文]. 长沙: 湖南大学, 2011.
- 18. Zheng, Y. and Deng, S. (2015) Failure Probability Model considering the Effect of Intermediate Principal Stress on Rock Strength. Mathematical Problems in Engineering, 2015, Article ID: 960973. http://dx.doi.org/10.1155/2015/960973
- 19. Kawamoto, T., Ichikawa, Y. and Kyoya, T. (1988) Deformation and Fracturing Behaviour of Discontinuous Rock Mass and Damage Mechanics Theory. International Journal for Numerical and Analytical Methods in Geomechanics, 12, 1-30. http://dx.doi.org/10.1002/nag.1610120102
- 20. 薛云亮, 李庶林, 徐宏斌, 等. 考虑残余强度的岩石损伤统计本构模型[C]//中国水利学会. 第二届中国水利水电岩土力学与工程学术讨论会论文集: 2008年卷. 武汉: 武汉大学学报: 工学版: 2008, 7.