Hans Journal of Civil Engineering
Vol.07 No.04(2018), Article ID:25251,8
pages
10.12677/HJCE.2018.74064
Study on the Influence of Force on Cement Asphalt Pavement Asphalt Pavement
Yanchang Yang1, Hongtao Li2, Liang Li3
1Luohe Highway Administration Bureau, Luohe Henan
2Luohe Highway Engineering Construction Corporation, Luohe Henan
3Changsha University of Science and Technology, Changsha Hunan

Received: May 12th, 2018; accepted: May 25th, 2018; published: Jun. 1st, 2018

ABSTRACT
This article has taken the example of the asphalt pavement of the Shanglin Interchange over the Mabin (Laibin-Mashan) Expressway as an example to establish a finite element model of the beam. The calculation is based on the tensile stress at the top of the pavement and the shear stress between the layers. Comparing three different pavement schemes, the effects of different driving conditions and temperatures on the asphalt pavement stress were analyzed. The results show that the advantages of the tensile structure of flip-type structure and flip-type resistance to thermal stress are better than other structures.
Keywords:Bridges, Cement Concrete Bridge Pavement, Stress
水泥砼桥面沥青铺装受力影响研究
杨彦昌1,李红涛2,李良3
1漯河市公路管理局,河南 漯河
2漯河市公路工程建设总公司,河南 漯河
3长沙理工大学,湖南 长沙

收稿日期:2018年5月12日;录用日期:2018年5月25日;发布日期:2018年6月1日

摘 要
本文以来马(来宾–马山)高速公路上林互通式立交桥沥青铺装工程为例,建立梁体有限元模型,以铺装层层顶拉应力和层间剪应力为计算指标,通过对比三种不同铺装方案,分析不同行车状况、温度对沥青铺装受力的影响。结果表明倒装式结构抗拉的优点以及倒装式抵抗温度应力效果较其他结构好。
关键词 :桥梁,水泥砼桥面铺装,应力

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前,桥面铺装层的损坏引起人们的广泛关注,如何提高水泥混凝土桥面铺装层结构的力学性能和耐久性能,成为一个亟待解决的问题 [1] 。桥面铺装层在车辆荷载、自然环境和自身材料等多重因素影响下,处于复杂的应力应变状态中,同时沥青混凝土与桥面板之间粘结力过小,剪应力超过层间最大剪应力时,使铺装层在水平方向产生相对位移从而产生剪切破坏 [2] 。沥青混凝土为柔性材料,而水泥混凝土为刚性材料,性质上的差异导致二者的受力状态具有显著的间断性 [3] 。为使准确的模拟沥青铺装体系在服役期间的受力特性,本文采用有限元软件,建立箱梁桥混凝土桥面沥青铺装体系实体模型,分析车辆荷载、刹车情况和温度变化对沥青铺装体系受力情况的影响。
2. 有限元模型的建立
上林互通式立交桥上部结构采用预应力砼箱梁,分左右两幅,每幅由4个小箱室组成。箱梁高1.5 m,上开口宽1.75 m,下开口宽1 m,两相邻箱室中心距为3 m,肋板厚0.18~0.20 m。跨径为25 m,在支座处设置横隔板。设计采用双层式沥青铺装。
横向选取一幅桥面,纵向选取两跨建立三维有限元模型(见图1)。受力所关注的沥青铺装层、砼现浇调平层和砼面板采用八节点单元,箱室和横隔板采用四节点单元,以减少单元数量,提高计算效率。在轮载作用区域及其附近细化网格尺寸,其余区域网格尺寸较粗。建模时作如下假定:各结构层之间完全连续,不计结构自重的影响;所有材料均为均匀且各向同性的线弹性材料;对箱梁底部支座进行约束,无横桥向(X向)、纵桥向(Y向)和竖向(Z向)位移。
依照现行规范,采用公路-I级荷载,考虑超载因素的影响,取 30%冲击系数,轮载接地压力为0.91 Mpa。取双矩形均布荷载模拟单轴双轮荷载,单轮接地面积为0.20 × 0.25 m2,两轮间距为0.10 m,轮载模型见图2。
桥面板上的铺装结构分为水泥砼调平层、沥青混合料铺装下层及上层。铺装体系各结构层计算参数见表1。

Figure 1. Finite element model
图1. 有限元模型

Figure 2. Double wheel uniform load (unit: cm)
图2. 双轮均布荷载(单位:cm)
Table 1. Bridge deck pavement system material parameters
表1. 桥面铺装体系材料参数
3. 行车状况对沥青铺装体系受力的影响
双层式沥青铺装所选用沥青混合料各不相同,根据所选沥青混合料种类,可将铺装结构组合分为:正装式结构、倒装式结构和等厚结构,研究这三种组合形式在不同行车状况下各自组合方案的受力特点的参数取值如表2所示。
3.1. 车辆超载对沥青铺装体系受力的影响
在考虑30%冲击系数的基础上 [4] ,对比分析不超载、超载20%、40%、60%、80%和100%条件下,沥青铺装体系受力情况。
在有限元计算中模拟超载现象,不但要增加垂直荷载,还应增加轮载作用面积。根据式(2.1)计算不同超载率的轮胎接地压力,再由式(2.2)确定轮载作用面积,因轮载横向边长不会变化仍为20 cm,据此即可求得纵向边长 [2] [3] 。计算结果如表3所示。
(2.1)
式中: ——超载车辆轴载(kN);
——超载车辆轮胎接地压强(MPa);
——标准轴载(kN);
——标准轴载轮胎接地压力(MPa)。
(2.2)
式中:s——轮载作用面积(cm2)。
不同超载率条件下,各方案沥青铺装体系受力情况,计算结果如图3、图4所示。
由图3、图4分析可知,随着超载率的增加,各项应力与超载率较好的线性增加。其中,层顶最大拉应力大小为:方案一 > 方案三 > 方案二,并且随着超载率的增加,同等情况下各方案间差异又继续扩大的趋势,在超载率到达100%时,层顶最大拉应力达到了0.5488 MPa;界面最大剪应力大小为:
Table 2. Different paving structure composite material parameters
表2. 不同铺装结构组合材料参数
Table 3. Load calculation parameters corresponding to different overload rates
表3. 不同超载率对应的荷载计算参数

Figure 3. Effect of overload rate on the maximum tensile stress at the top of three kinds of schemes
图3. 超载率对三种方案层顶最大拉应力的影响
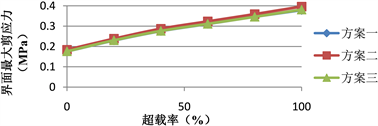
Figure 4. Effect of overload rate on the interface maximum shear stress of three schemes
图4. 超载率对三种方案界面最大剪应力的影响
方案二 > 方案三 > 方案一,但是同等情况下各方案间差距较小,最大不过4.4%。因此,采用铺装方案一(即正装式结构)时需要特别注意铺装上层沥青混合料抗拉强度,而不论何种方案都需注意界面抗剪。
通过计算结果,拟合得到车辆超载时三种不同铺装方案应力变化曲线公式,如式(2.3)~式(2.8)。
方案一(即正装式结构):
(2.3)
(2.4)
方案二(即倒装式结构):
(2.5)
(2.6)
方案三(即等厚式结构):
(2.7)
(2.8)
式中:X——超载率(%)。
3.2. 车辆刹车对沥青铺装体系受力的影响
车辆刹车通常会导致产生铺装层变形类病害以及防水粘结层粘结失效 [5] 。在建模时同时考虑垂直和水平荷载,这里引入水平摩阻系数,由式2.9可求得水平荷载。
(2.9)
式中:F——水平荷载(kN);
P——车辆垂直荷载(kN);
f——水平摩阻系数。
水平摩阻系数跟桥面的粗糙程度、汽车的速度、汽车的轮胎样式等因素有关 [6] 。为分析车辆刹车对沥青铺装体系受力的影响,分别考虑水平摩阻系数为0、0.1、0.2、0.3、0.4和0.5条件下,各方案沥青铺装体系受力情况,计算结果如图5、图6所示。
由图5、图6分析可知,当水平摩阻系数超过0.2之后,层顶最大拉应力迅速增加,三种不同方案之间差别较大,大小排序为:方案一 > 方案三 > 方案二;而界面最大剪应力与水平摩阻系数呈较好的线性相关,并且三种方案相差较小,最大仅2.7%,尤其是方案一与方案三几乎没有差别,大小排序为:方案二 > 方案三 > 方案一。
通过计算结果,拟合得到车辆刹车时三种不同铺装方案应力变化曲线公式,如式2.10~式2.15。
方案一(即正装式结构):
(2.10)
(2.11)
方案二(即倒装式结构):
(2.12)
(2.13)
方案三(即等厚式结构):
(2.14)
(2.15)

Figure 5. Effect of horizontal friction coefficient on the maximum tensile stress at the top of three kinds of schemes
图5. 水平摩阻系数对三种方案层顶最大拉应力的影响
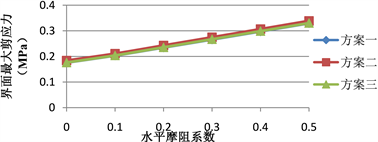
Figure 6. Effect of horizontal friction coefficient on the interface maximum shear stress of three schemes
图6. 水平摩阻系数对三种方案界面最大剪应力的影响
4. 温度变化对沥青铺装体系受力的影响
沥青混凝土属于粘弹性材料,当温度缓慢变化时,温度应力会出现应力松弛现象 [7] ;但短时温度急剧变化会增大温度应力,可能会导致铺装层开裂。
4.1. 温度传递基本理论和边界条件
依照傅里叶定律,建立空间坐标系下热传导微分方程如下:
(3.1)
式中:q——热流密度(W/m2);
∆T——温度梯度(℃/m);
k——导热系数(W/m℃);
t——作用时间(s)。
具体展开来有:
(3.2)
式中: ——分别为沿 方向的单位向量。
将上式简化为各方向分量形式:
(3.3)
假设无内热源存在,依照能量守恒定律得出导热系数k为常数时热传导微分方程:
(3.4)
式中:α——导热系数(m2/s)。
即:
(3.5)
对于第一类边界条件,在边界Si上有:
(3.6)
其中, 可看作是与坐标有关或时间t有关的函数,或者为某一常数,当这一常数为0时,称之为第一类边界条件。
4.2. 温度应力分析
选用温度传导的第一类边界条件,计算了温度变化分别为−5℃、−10℃、−15℃和−20℃时,各方案沥青铺装体系受力情况,计算结果如图7、图8所示。
由图7、图8分析可知,各方案层顶最大拉应力随着温度减低而增大,都呈较好的线性关系,这也表明了在低温季节铺装结构顶面承受着较大拉应力,一旦超过铺装材料强度容许值,就会产生开裂。综合计算结果来看,各方案所受温度应力排序为:方案一 > 方案三 > 方案二,说明在这三种方案中,方案二(即倒装式结构)抵抗温度应力效果较好。
通过计算结果,拟合得到温度变化时三种不同铺装方案应力变化曲线公式,如式3.7~式3.12。
方案一(即正装式结构):
(3.7)
(3.8)
方案二(即倒装式结构):
(3.9)
(3.10)
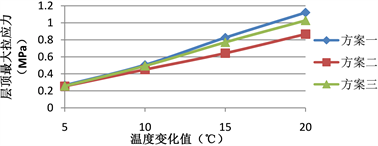
Figure 7. Effect of temperature change on the maximum tensile stress at the top of three kinds of schemes
图7. 温度变化对三种方案层顶最大拉应力的影响

Figure 8. Effect of temperature change on the interface maximum shear stress of three schemes
图8. 温度变化对三种方案界面最大剪应力的影响
方案三(即等厚式结构):
(3.11)
(3.12)
式中:T——温度变化值(℃)。
5. 结论
通过建立有限元实体模型,对比行车状况和温度变化因素作用下对箱梁桥混凝土桥面沥青铺装体系受力的影响。通过分析,得出如下结论:
1) 超载作用对铺装层顶影响较大,应严格控制超载现象的发生;
2) 当水平摩阻系数超过0.2之后,层顶最大拉应力迅速增加;而界面最大剪应力与水平摩阻系数呈较好的线性相关,并且三种方案相差较小;
3) 各方案层顶最大拉应力随着温度减低而增大,都呈较好的线性关系,这也表明了在低温季节铺装结构顶面承受着较大拉应力,一旦超过铺装材料强度容许值,就会产生开裂。
考虑三种不同铺装方案在车辆超载、车辆刹车时以及温度急剧降低时的受力情况,表明倒装式结构抗拉的优点,同时倒装式结构抵抗温度应力效果较好。
文章引用
杨彦昌,李红涛,李 良. 水泥砼桥面沥青铺装受力影响研究
Study on the Influence of Force on Cement Asphalt Pavement Asphalt Pavement[J]. 土木工程, 2018, 07(04): 559-566. https://doi.org/10.12677/HJCE.2018.74064
参考文献
- 1. 朱敏清. 水泥混凝土桥梁铺装层受力特性分析[J]. 桥隧工程, 2017(3): 10.
- 2. 王光谱. 混凝土箱梁桥面铺装力学行为与结构优化设计[D]: [硕士学位论文]. 西安: 长安大学, 2017.
- 3. 杨坤. 沥青混凝土桥面铺装力学分析与试验研究[D]: [硕士学位论文]. 西安: 长安大学, 2015.
- 4. 孔铭. 水泥混凝土路面极限承载力研究[D]: [硕士学位论文]. 长沙: 湖南大学, 2006.
- 5. 李海军, 黄晓明. 重载条件下沥青路面按弯沉等效的轴载换算[J]. 公路交通科技, 2004(7): 5-8.
- 6. 黄晓明. 水泥混凝土桥面沥青铺装层技术研究现状综述[J]. 交通运输工程学报, 2014(1): 1-10.
- 7. 葛倩如. 玄武岩纤维高粘沥青桥面铺装层数值分析[D]: [硕士学位论文]. 杭州: 浙江大学, 2015.
