Open Journal of Transportation Technologies
Vol.
07
No.
06
(
2018
), Article ID:
27434
,
10
pages
10.12677/OJTT.2018.76045
Evaluation Method of Anti-Sliding Control Based on Analytic Hierarchy Process
Feng Diao, Wenliang Zhu, Lingguang Qin, Mengling Wu
Tongji University Railway and Urban Rail Traffic Academy, Shanghai

Received: Oct. 17th, 2018; accepted: Oct. 30th, 2018; published: Nov. 6th, 2018

ABSTRACT
Based on the HIL simulation platform and the research of existing WSP system evaluation, five design principles of WSP system performance evaluation method, including synthesis, comprehensiveness, adaptability, compulsion and repeatability, are put forward. Based on those principles, multi-index performance evaluation method of WSP system under different operating conditions as well as the standardization process of data processing is established.
Keywords:Train Anti-Skidding, AHP, Evaluation Method
基于层次分析法的列车防滑控制 评价方法
刁锋,朱文良,秦凌光,吴萌岭
同济大学铁道与城市轨道交通研究院,上海

收稿日期:2018年10月17日;录用日期:2018年10月30日;发布日期:2018年11月6日

摘 要
通过硬件在环仿真方法,基于对防滑系统评价研究现状的研究总结,提出了综合性、全面性、适应性、强制性、可重复性等五项防滑系统性能评价方法设计原则,并基于此设计了综合多个轮轨黏着工况下防滑系统性能表现的多指标评价方法,使用离差标准化的数据处理方法对各项指标值进行归一化处理,最后基于层次分析法确立了各黏着水平下指标值的权重取值,建立了完整的防滑系统性能评价各指标值量化计算过程,为防滑控制评价提供理论依据。
关键词 :列车防滑,层次分析法,评价方法

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前,对于列车防滑装置的性能评价,以各国法规为主,其中针对防滑器性能所提出的各类指标均为单一的合格性要求,无法利用其对防滑装置性能的优劣开展进一步分析与评价,且其多侧重对防滑装置工作时的制动距离进行评判,对于能体现制动过程经济性的耗风量、轮对磨损程度控制等指标多未进行综合考虑。
上海地铁一号线技术规格书中对地铁车辆防滑系统性能提出了防滑效率的概念。其防滑概念指在给定的工况下,防滑系统工作时的理想最短停车距离与实际运行停车距离的比值,效率越高,利用黏着的能力越强,防滑系统性能越优。关于防滑效率概念的实际应用,邬志伟、胡用生等人在其文章中提出了防滑效率几种不同的计算方法 [1] 。其中速度线性假设下的计算方法,比较接近实际,但实际上当滑行工况出现时,速度并非都随时间线性下降,基于此假设计算的防滑效率会比实际值偏大,甚至出现大于100%的情况,这显然是不科学的;基于线性假设下的计算方法用出现滑行时的黏着条件代表整个制动过程中的黏着水平进行计算,但由于实际工况中,轮轨黏着水平沿列车运行方向水平并不完全一致,因此用此种方法进行计算也存在一定的误差;平均加速度法中将轮轨黏着水平视为一个逐渐变化的物理量,将整个防滑过程的若干个减速度主峰值的平均值作为计算理想最短制动距离的基础,但这种选取方法仍存有大量的主观因素 [2] [3] 。
可见列车防滑器的工作性能评判标准仍较模糊,给防滑系统的设计、优化带来困难,本文拟提出一种列车防滑控制器性能评价方法,用于指导防滑器设计、改进其控制性能。
2. 硬件在环半实物仿真平台
列车防滑控制试验不同于正常工况制动试验,试验成本较高、可重复性差且安全系数较低,目前针对列车防滑控制的研究多基于硬件在环(HIL)半实物仿真方法,国内外已有诸多学者利用不同的模型和系统架构,开展了防滑控制试验研究,意大利的L. PUGI,M. MALVEZZI等人设计建造了MI-6测试装置 [4] [5] [6] ,韩国建国大学的Ho-Yeon Kim,Nam-Jin Lee等人也建立了基于dSPACE平台的防滑装置硬件在环仿真平台 [7] [8] 。
本文利用的防滑控制半实物仿真平台系统构架见图1,工作原理如下:试验开始前进行仿真工况、模型参数的设定,并将车辆纵向动力学模型、轮轨黏着力模型、气制动系统模型烧录至dSPACE实时仿真平台中,车辆载重信息经dSPACE平台发送给BCU (制动控制单元);司控器发出制动指令信息到BCU,BCU在接受到制动指令信息后根据当前制动级位信息及车辆载荷信息计算当前所需制动力及对应EP电流值发送至dSPACE平台,EP电流值经信号采集部分传输至气制动系统模型部分作为目标制动力控制制动缸压力上升;制动缸压力信息经基础制动装置模型换算为制动夹钳夹紧力施加于车轮;车辆纵向动力学模型负责模拟车辆实际运行中的各类制动状态信息,如车速、轴速等;模型中的轴速、制动缸压力等信息经dSPACE平台信号发生和信号调理模块传送至制动控制单元和操作台上位机人机交互界面以供运算及信息显示。BCU根据接受到的轴速信息判定当前车辆是否处于滑行状态,如判定发生滑行,则发出防滑阀控制信号,经dSPACE平台信号采集系统采集至气制动模型中,控制防滑阀动作,模拟制动缸排气、保压、充气动作,实现列车防滑控制。
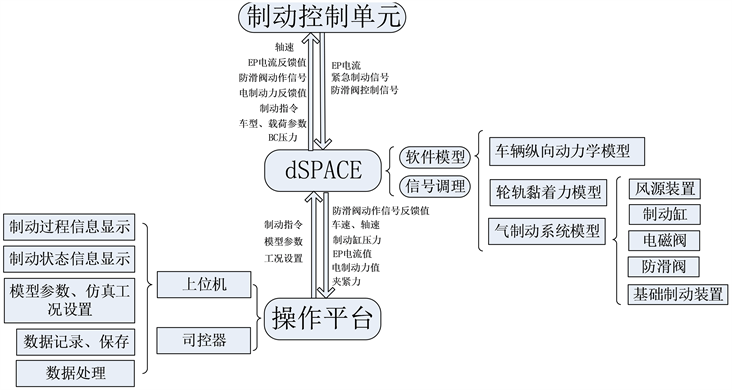
Figure 1. HIL simulation platform framework for anti-skid control
图1. 防滑控制半实物仿真平台架构
整个仿真平台从制动距离、速度曲线、各轴速度差分布三个方面与实车试验数据(制动初速103 km/h,制动级位为紧急制动,轨面喷洒防冻液)进行对比进行了验证:
1) 列车制动距离试验值为733米,制动距离仿真值为748米,误差约为2%,满足对试验中制动距离模拟的相关要求;
2) 制动过程中任一时刻仿真车速与试验车速最大差值为1.06 km/h,满足要求;
3) 各轴轴速仿真值与试验值对比分析结果见表1,其中第3轴防滑判据较为特殊,不同于其他三根轴,在此不作分析。速度差均值统计误差最大为2.91%,标准差统计误差最大为4.81%,模型性能满足要求。
Table 1. Statistical comparison between simulation values and experimental values
表1. 各轴速度差仿真值与试验值统计对比
3. 评价方法设计原则
目前列车气制动防滑控制系统的工作原理为在轮轨黏着条件变差、列车发生滑行时,降低制动力,减少轮轨滑行的产生。这种控制方式的关键在于滑行状态判别阈值及防滑阀动作参数的选取。本文从综合性、全面性、适应性、强制性、可重复性等原则出发,建立列车防滑性能评价方法。
1) 综合性原则
列车防滑控制系统的性能体现在各个方面,除了制动距离、制动减速度等安全性指标,还有对风源系统的负载、对轮轨磨耗的控制、防滑阀寿命的合理利用等经济性指标,当前实际应用中较多关注制动距离这一单一指标,不能全面体现防滑系统性能好坏。
2) 全面性原则
轮轨间黏着条件受雨、雪、树叶、油等污染物影响较大,且不同污染物造成影响差别较大,目前列车上应用的多为单一无针对性的控制策略,未对不同轮轨工况进行区别控制,同一个防滑控制器,在不同轮轨黏着条件下,其控制效果有较大差别。因而某一种轮轨黏着条件下的性能表现不能完整反映,对于防滑系统性能的评价应是对其不同轮轨黏着水平条件下性能表现的综合评价。
3) 适应性原则
列车运行线路所处地域、气候的不同,导致列车不同轮轨黏着水平分布不同。多雨的江南地区和多冰雪的东北高寒地区相比,东北高寒地区的轮轨黏着水平相对更为恶劣,这也决定了不能对所处不同运营环境的防滑控制系统应用同一种评判标准,防滑系统性能评价方法基于用户的需求和偏好及列车所处实际运营环境建立,具备一定的适应性。
4) 强制性原则
当前世界各国的标准和规范文件,都对列车制动系统中防滑装置的性能做了部分强制性要求,防滑系统性能的评价方法中应能体现相关标准对其的强制性要求。
5) 可重复性原则
基于实车试验的防滑系统性能测试成本高,试验过程中各参数如轮轨间实际黏着系数、实际利用黏着系数、耗风量、黏着力等参数不易测量;受实际条件影响,试验环境的可重复性较差,难以提供较为标准统一的测试环境,而可重复性是系统性能测试和评价的前提,故防滑系统性能评价的试验基础应满足可重复性原则。
4. 防滑控制系统性能评价方法建立
从以上几个原则出发,基于防滑控制半实物仿真平台,建立图2的防滑系统性能评价方法,并使用图3的数据采集处理过程。在0.05~0.08不同黏着水平(因轮轨黏着系数并非定值,而是随车速、滑移率等参数变化的变化值,因此无法用具体数值进行描述,本文中均以最大黏着水平代替,最大黏着指当前条件下可能出现的最大轮轨黏着水平)下开展相关测试试验,从列车制动全过程黏着系数利用率、耗风量扩大比、轮对滑移做功、防滑阀动作次数等四个角度对防滑性能进行评价,综合反映其各方面性能,利用离差标准化的处理方法将各指标归一化,使用层次分析法确定不同轮轨黏着水平下各指标值的权重系数,最终得到能够反映防滑系统不同方面性能的指标值。
4.1. 防滑系统性能评价指标设计
4.1.1. 黏着系数利用率指标
防滑控制黏着系数利用率是列车对轮轨黏着条件利用情况的最本质体现,直接影响了列车制动距离、平均减速度、轮对滑移率控制等,利用防滑控制半实物仿真平台,建立轮轨黏着力模型模拟轮轨接触情况 [9] [10] ,可使得列车制动全过程中的黏着系数参数变得可控且可重复,使得制动全过程的黏着系数利用率的计算成为可能。

Figure 2. Schematic diagram of performance evaluation method for WSP system
图2. 防滑系统性能评价方法示意图
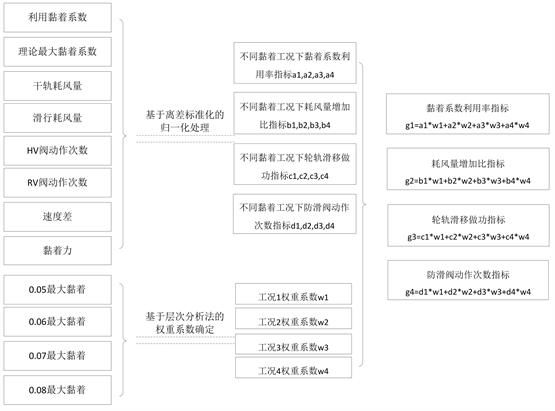
Figure 3. Data acquisition process for evaluation method
图3. 防滑评价方法数据采集处理过程
不同于实车线路试验,在仿真平台试验中,轮轨间实际黏着系数和最大黏着系数均为可测可知量,通过计算最大黏着利用时的制动距离,实际制动距离,则列车制动全过程黏着系数利用率为:
(1)
4.1.2. 耗风量增加比指标
在滑行工况制动过程中,由于防滑阀的不断动作,制动缸不断在排气、保压、充气状态间切换,压缩空气消耗量会急剧上升,因此制动过程的耗风量可以作为评判防滑系统性能的一个重要指标。但制动过程中的耗风量受制动缸体积、管路、目标制动缸压力等因素影响,为排除由系统本身固有特性造成的影响,采用滑行工况时相对于干轨制动工况的耗风量的增加比进行评价,同一黏着水平下耗风量增加比越少,耗风量则相对较少,认为其经济性越高。
以中继阀输出的气体体积作为耗风量,制动过程耗风量的计算公式如下:
(2)
其中 为气体体积流量;干轨工况下耗风量为 ,滑行工况下耗风量为 ,则耗风量增加比 的计算公式为:
(3)
4.1.3. 轮对滑移做功指标
当速度一定时,轮轨间黏着系数是随滑移率变化的一条曲线,并存在峰值点,合理的控制轮对滑移能更大地利用黏着。干轨工况下,轮速与车速间速度差较小,轮对滑移率值较小,因轮轨相对速度产生的滑移做功也较小;在滑行工况中,轮对滑移率可能达到20%甚至更高,也使得轮对滑移做功值急剧上升,单个滑行周期内的轮对滑移做功值直接影响着轮对和轨面的磨耗水平,如控制不当甚至可能导致轮对抱死和擦轮,相关标准中也有对于单个滑行阶段内轮对滑移做功值的要求 [11] ,因此可以将轮对滑移做功作为一个防滑系统性能指标。通过轮对速度差、黏着力建立轮对滑移功率表达式:
(4)
其中 为实际利用黏着系数, 为轮轨间正压力, 为轮轨间速度差,滑移做功 为:
(5)
以防滑阀开始动作为开始信号,防滑阀停止动作为结束信号确定列车当前是否处于滑行状态,分别计算每次滑行周期内的轮对滑移做功 及整个制动过程中的轮对滑移做功平均值 作为轮对滑移做功指标值:
(6)
其中 为滑行阶段次数。
4.1.4. 防滑阀动作次数指标
防滑阀的性能好坏直接决定了BCU的防滑控制指令能否被准确执行,一次滑行工况中防滑阀的动作次数可能有数十次甚至上百次,动作次数直接影响着电磁阀寿命,因此制动过程中的防滑阀动作次数可以作为一个防滑系统性能指标。以电磁阀控制信号由低到高(0~1)记为动作一次,分别统计一次滑行工况制动全过程中一节车各轴排气电磁阀和保压电磁阀的动作次数 ,取各轴防滑阀的平均动作次数作为防滑动作次数指标值:
(7)
4.2. 评价指标的归一化处理
不同评价指标具有不同的量纲和量级,对数据进行归一化处理来消除指标之间的量纲影响。Z-score标准化方法是基于原始数据的均值和标准差进行数据的标准化,经过处理的数据符合标准正态分布 [12] ;Min-Max标准化方法也叫离差标准化,是对原始数据进行线性变换;Logistic标准化通过以10为底的log函数转换,实现数据标准化 [13] 。本文选用离差标准化方法作为各性能指标的归一化处理方法,使其结果映射到0~1之间,转换公式如下:
(8)
对于黏着系数利用率指标,取最小值 ,最大值 。当指标值为0时,说明列车制动距离无限长,即车辆无法停止;当指标值为1时,表示在当前黏着工况下,防滑系统对于轮轨黏着完全利用,制动距离为理论最短制动距离,归一化后指标 为:
(9)
对于耗风量增加比指标,取最小值 ,最大值 。当指标值小于等于0时,表明制动耗风量不符合EN15595标准对防滑器模拟台架试验120 km/h初速工况下耗风量扩大比最高为25的规定;当指标值为1时,表明相对干轨工况,在发生滑行时未产生额外的空气消耗,归一化后指标 为:
(10)
对于滑移做功指标,取最小值 ,最大值 。当指标值小于等于0时,轮对滑移做功值不符合EN15595对于单个滑移阶段内轮轨间滑移做功不大于26 kJ的规定;指标值越高则说明轮轨间滑移做功越小,轮轨磨耗和发生擦轮的风险也较小,归一化后指标 为:
(11)
对于防滑阀动作次数指标,取最小值 ,最大值 ,相关国家标准中暂无对于滑行过程中防滑阀动作次数的规定,该项指标参数的选取参考仿真试验及部分实车试验数据防滑阀动作情况,当指标值小于等于0时,说明防滑阀动作次数过多,有过热损坏的风险,指标值越高则说明防滑系统性能表现越好,归一化后指标 为:
(12)
4.3. 基于层次分析法的各黏着水平指标值权重确立
层次分析法应用的关键在于根据应用对象的特点和性质将问题层次化,将分层后的应用对象分解为不同的元素,再根据各层因素之间的关联性按不同的层次聚集组合,最终构建出一个多层次的分析结构模型,进而把复杂的系统分析过程转换为各层之间重要程度的排序。
为了将各层元素之间的相互比较判断程度定量化,层次分析法中引入了1~9的比率标度方法如表2,将判断结果以矩阵的形式呈现出来,即判断矩阵。判断矩阵构建完成,通过计算判断矩阵的最大特征根及其对应的特征向量,即可得到某层元素相对于其上一层元素的相对重要性权重值。但在构建判断矩阵时,决策者一般不可能给出完全精确的比较判断,因此在层次分析法中,引入了对判断矩阵的一致性校验步骤,可以将决策者判断的不一致性检验出来,以达到检查和保持决策者判断过程一致性的目的 [14] [15] 。基于以上原理,对于防滑系统在各黏着水平下的指标值确立应用层次分析法,层次结构如图4。
Table 2. Judgement matrix scale and its meaning
表2. 判断矩阵标度及其含义

Figure 4. Hierarchical structure establishment
图4. 层次结构建立
本文对基于不同轮轨黏着水平构建的判断矩阵中各元素标度值的选择遵循以下原则:以列车实际运行中可能遇到相应黏着水平工况概率的高低作为比较的依据,参考可能导致轮轨低黏着条件的各类天气出现的概率,调研听取专家意见。各元素标度值的选择体现了对于不同轮轨黏着条件的偏好程度,可根据实际应用情况和需求进行调整。各元素标度值填充完整后的判断矩阵如下:
其中B1,B2,B3,B4依次表示0.05最大轮轨黏着水平、0.06最大轮轨黏着水平、0.07最大轮轨黏着水平、0.08最大轮轨黏着水平等试验工况。
层次分析法的应用中选择判断矩阵元素标度值时,为保持决策者判断思维的一致性,需对判断矩阵一致性进行检验,判断矩阵A需要满足如下关系:
根据矩阵理论,判断矩阵在满足上述完全一致性条件下,具有唯一非零的、最大的特征根 ,且除 外,其余特征根均为零。因此,层次分析法应用计其余特征根均为零。因此判断矩阵的特征根及特征向量的求解非常关键,本文采用方根法进行求解:
1) 计算判断矩阵每一行元素的积,其中 为矩阵阶数:
(13)
2) 计算各行的 次方根值: ;
3) 将向量 归一化,计算如下,即为所求各指标的权重系数:
(14)
4) 判断矩阵的最大特征根为:
(15)
计算一致性指标 及一致性比率 校验判断矩阵是否具有满意的一致性。其中 , , 为平均随机一致性指标,其取值见表3,当 时,即可以认为判断矩阵具有满意的一致性,否则需要调整判断矩阵,以使之具有满意的一致性。
Table 3. Mean random consistency index RI
表3. 平均随机一致性指标RI
根据上述计算步骤,得出 ,一致性校验结果 ,通过校验,即判断矩阵具有满意的一致性。计算得出上述判断矩阵下的各轮轨黏着工况下的指标权重值依次为: 。
5. 结束语
1) 基于综合性、全面性、适应性、强制性、可重复性等原则,从列车制动全过程黏着系数利用率、耗风量扩大比、轮对滑移做功、防滑阀动作次数等四个角度建立列车防滑系统评价方法;
2) 从多种轮轨黏着水平下对其性能进行考虑,使用min-max离差标准化及层次分析法对各指标进行归一化和标准化处理;
3) 确立了各性能指标所需采集量、计算方法以及数据归一化过程中各参数值的选取;
4) 完成层次分析法判断矩阵的建立及各指标权重的计算和一致性校验。
基金项目
国家自然科学基金资助项目(U1534205)。
文章引用
刁 锋,朱文良,秦凌光,吴萌岭. 基于层次分析法的列车防滑控制评价方法
Evaluation Method of Anti-Sliding Control Based on Analytic Hierarchy Process[J]. 交通技术, 2018, 07(06): 371-380. https://doi.org/10.12677/OJTT.2018.76045
参考文献
- 1. 邬志伟, 胡用生, 沈钢, 朱小娟. 城市轨道车辆牵引、制动与防滑系统的效率研究[J]. 城市轨道交通研究, 1998, 1(2): 32-36.
- 2. 陈伟, 周军, 王新海, 曹宏发, 韩晓辉. 和谐号动车组制动防滑控制理论和试验.[J]. 铁道机车车辆, 2011, 31(5): 32-37.
- 3. 李云峰. 城轨车辆空气制动防滑控制方法[J]. 铁道车辆, 2011, 49(12): 38-40+6.
- 4. Pugi, L., Malvezzi, M., Tarasconi, A., Palazzolo, A., Cocci, G. and Violani, M. (2006) Hil Simulation of WSP Systems on Mi-6 Test Rig. Vehicle System Dynamics, 44, 843-852.
- 5. Conti, R., Meli, E., Ridolfi, A. and Rindi, A. (2014) An Innovative Hardware in the Loop Architecture for the Analysis of Railway Braking under Degraded Adhesion Conditions through Roller-Rigs. Mechatronics, 24, 139-150. https://doi.org/10.1016/j.mechatronics.2013.12.011
- 6. Allotta, B., Meli, E., Ridolfi, A. and Rindi, A. (2014) Development of an Innovative Wheel-Rail Contact Model for the Analysis of Degraded Adhesion in Railway Systems. Tribology International, 69, 128-140. https://doi.org/10.1016/j.triboint.2013.09.013
- 7. Kang, C.-G., Kim, H.-Y., Kim, M.-S. and Goo, B.-C. (2009) Real-Time Simulations of a Railroad Brake System Using a dSPACE Board. IEEE ICCAS-SICE, Fukuoka, 18-21 August 2009.
- 8. Kang, C.-G. (2007) Analysis of the Braking System of the Korean High-Speed Train Using Real-Time Simulation. Journal of Mechanical Science and Technology, 21, 1048-1057. https://doi.org/10.1007/BF03027654
- 9. 曹宏发, 周军, 陈伟. 基于仿真技术的防滑试验方法研究[J]. 铁道机车车辆, 2015, 35(3): 11-16.
- 10. Polach, O. (2005) Creep Forces in Simulation of Traction Vehicle Running of Adhesion Limit. Wear, 258, 992-1000. https://doi.org/10.1016/j.wear.2004.03.046
- 11. European Committee for Standardization (2009) BS EN 15595. Railway Applications Braking Wheel Slide Protection. CEN Management Centre, London.
- 12. 吴云鼎, 解保生, 丁仲鹃. 实时定量PCR的数据归一化方法[J]. 昆明医科大学学报, 2013, 34(3): 160-164.
- 13. 汤荣志, 段会用, 孙海涛. SVM训练数据归一化研究[J]. 山东师范大学学报(自然科学版), 2016(4): 60-65.
- 14. 王丽. 基于AHP的城市旅游竞争力评价指标体系的构建及应用研究[J]. 地域研究与开发, 2014, 33(4): 105-108.
- 15. 田辉平. 基于层次分析法和聚类分析法相结合的评价方法[J]. 华东经济管理, 2007(8): 126-128.
