Advances in Energy and Power Engineering
Vol.03 No.04(2015), Article ID:16063,9 pages
10.12677/AEPE.2015.34011
Solution of Ill-Conditioned Load Flow for Power System and the Drawing of PV-Curve Based on Tensor Method
Shan Jiang1*, Yimeng Du2
1State Grid Shaanxi Economic Research Institute, Xi’an Shaanxi
2School of Electrical Engineering, Xi’an Jiaotong University, Xi’an Shaanxi
*通讯作者。
Email: *13193332511@163.com
Received: Aug. 25th, 2015; accepted: Sep. 15th, 2015; published: Sep. 21st, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper presents a new method called tensor method to solve the ill-conditioned load flow of power system and draw the PV-curve. The tensor method bases each iteration on the quadratic model of the nonlinear function. Compared to Newton method, the model requires hardly more storage or arithmetic operations per iteration. The tensor method is as effective as Newton method on well-conditioned problems, and performs better on ill-conditioned problems for drawing the PV-curve. IEEE-5, 11, 13 bus systems are calculated with both tensor method and Newton method. It is found that tensor method is better than Newton method.
Keywords:Power System, Ill-Conditioned Load Flow, Tensor Method, PV-Curve

基于张量法的电力系统病态潮流求解与PV曲线绘制
姜山1*,杜一盟2
1国网陕西省电力公司经济技术研究院,陕西 西安
2西安交通大学电气工程学院,陕西 西安
Email: *13193332511@163.com
收稿日期:2015年8月25日;录用日期:2015年9月15日;发布日期:2015年9月21日

摘 要
本文提出一种求解电力系统病态潮流并绘制PV曲线的新方法,称之为张量法。张量法基于非线性方程组的二次模型进行迭代。相对于传统牛顿法,张量法在每次迭代中几乎不需要更多的存储空间和运算量。对于良态系统潮流的计算,张量法的计算效率与传统牛顿法相差不多,对于病态的潮流问题,张量法绘制PV曲线的运算效率和可靠性都远高于牛顿法。对IEEE-5, 11, 13节点系统进行了潮流计算,结果表明张量法优于牛顿法。
关键词 :电力系统,病态潮流,张量法,PV曲线

1. 引言
潮流计算是分析电力系统稳态运行情况的一种基本电气计算,电力系统潮流的计算中普遍使用的方法为牛顿-拉夫逊法,此方法收敛速度快,但对迭代初值要求高[1] 。在绘制系统PV曲线时,随着功率P的增大,某些潮流计算使用常规方法可能会不收敛,成为病态潮流。
病态潮流的出现主要有以下两方面的原因:
1) 潮流计算的解远离平启动点,使得在平启动下使用常规潮流计算方法无法求出。
2) 在系统重负荷、接近功率极限点时,系统的雅克比矩阵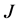 出现奇异或接近奇异 [2] 。
出现奇异或接近奇异 [2] 。
求解电力系统的病态潮流绘制PV曲线,需要特殊的计算方法。在牛顿–拉夫逊法的基础上,学者们已经提出了两种经典算法,即最佳乘子法和非线性规划法。
最佳乘子法由岩本伸一提出 [3] ,被认为是一种比较成功的求解病态潮流的方法。其基本原理是在每次迭代中使用牛顿法求解出修正量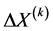 后,不直接去修正
后,不直接去修正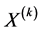 ,而是乘以最佳乘子
,而是乘以最佳乘子 再进行修正,
再进行修正,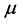 的取值要满足。
的取值要满足。

最佳乘子法具有如下优点:
1) 最佳乘子法可以作为一个子程序很容易的嵌入到牛顿法中。
2) 最佳乘子法是一种较为准确、实用的病态潮流计算方法,当潮流不收敛时, 趋向于零,保证了潮流计算的不发散。
趋向于零,保证了潮流计算的不发散。
尽管如此,最佳乘子法还是没有从本质上解决算法对初值的敏感,此外,当潮流方程无可行解时,虽然最佳乘子法适当地停止了计算,但并不能给出节点功率不平衡的信息,最佳乘子法存在缺陷。
对于病态的潮流问题,可以将其转化为求解一个非线性规划的问题 [4] 。通常将目标函数定义为
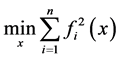 。当潮流有解时,目标函数趋向于零,如果无解,则目标函数停留在一个不为零的正值上,
。当潮流有解时,目标函数趋向于零,如果无解,则目标函数停留在一个不为零的正值上,
得到的是最小二乘解。
计算的关键在于求解构造的非线性规划问题,但总的说来,非线性规划法求解病态潮流计算量较大,求解复杂,因而实用性不强。
2. 张量法简介
基于以上分析,本文提出了一种新的求解病态潮流并绘制PV曲线的方法,叫做张量法。张量法在每次迭代计算中使用了非线性方程组的二次展开项,适合计算由于雅克比矩阵奇异所引起的病态潮流问题。相对于传统的线性模型,张量模型在每次迭代中几乎不需要更多的存储空间和计算量,而且无论在计算奇异或非奇异问题时,效率都高于传统的线性模型 [5] 。
张量模型基于 在当前迭代点
在当前迭代点 的二次展开项来建立模型,即:
的二次展开项来建立模型,即:

其中 为一个三维数组,
为一个三维数组, 通常被成为张量,张量法的名称由此而来。而
通常被成为张量,张量法的名称由此而来。而 ,
,
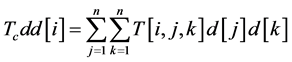
显然我们可以选取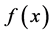 在
在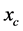 处的二阶泰勒展开项
处的二阶泰勒展开项 作为
作为 [6] 。然而这样做会使得计算量和存储量大幅增加,因此,用
[6] 。然而这样做会使得计算量和存储量大幅增加,因此,用 作为张量
作为张量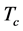 不具有可行性,我们需要一个简单实用的张量模型。
不具有可行性,我们需要一个简单实用的张量模型。
为得到合适的张量模型,需要内插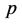 个已经求出的迭代点
个已经求出的迭代点 ,每个点都满足等式:
,每个点都满足等式:
 (1)
(1)
其中: 。
。
通常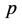 取1,实际经验表明,当
取1,实际经验表明,当 大于1时,对计算的改进作用不大,反而增加了数据存储量。
大于1时,对计算的改进作用不大,反而增加了数据存储量。
令 ,则可以构造
,则可以构造 满足下式:
满足下式:
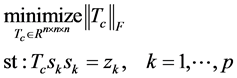 (2)
(2)
可以证明,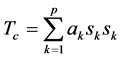 满足(2)式[5]
,其中定义矩阵
满足(2)式[5]
,其中定义矩阵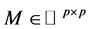 ,矩阵元素满足
,矩阵元素满足 ,定义矩阵
,定义矩阵 ,向量
,向量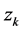 为其第k列元素,
为其第k列元素, 。定义矩阵
。定义矩阵 ,则
,则 的每一列即为向量
的每一列即为向量 ,
, 。
。 表示一个秩一向量,它满足等式:
表示一个秩一向量,它满足等式:

所以张量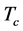 由
由 个秩一向量相加构成,将
个秩一向量相加构成,将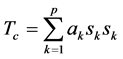 带入式(1),得到张量模型:
带入式(1),得到张量模型:
 (3)
(3)
式(3)是可以有效的形成、存储、计算的张量模型。相对于经典的线性模型,其仅需要额外存储2p个n维向量ak、sk,以及2p个n维向量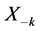 、
、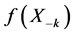 。计算速度方面,相对于线性模型每次迭代至少所需的n3/3次加法和乘法运算,张量法每次迭代仅需要n2.5次加法和乘法。
。计算速度方面,相对于线性模型每次迭代至少所需的n3/3次加法和乘法运算,张量法每次迭代仅需要n2.5次加法和乘法。
3. 张量法在电力系统潮流计算中的应用
在本章中,我们将提出一种实用算法来使用张量法进行电力系统潮流与绘制PV曲线。在计算中,我们使用直角坐标,平启动计算,得到计算结果后作为下次计算的初值从而绘制PV曲线。
令 (母线数),定义
(母线数),定义 为电压实部,虚部组成的向量,
为电压实部,虚部组成的向量,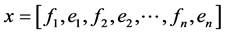 。定义
。定义 为功率适配量,
为功率适配量, 为
为 节点数,
节点数, 。
。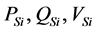 为母线
为母线 的设定有功,无功,电压。
的设定有功,无功,电压。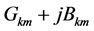 为导纳矩阵的第
为导纳矩阵的第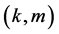 元素,我们可以得到直角坐标下的潮流方程为
[1] :
元素,我们可以得到直角坐标下的潮流方程为
[1] :
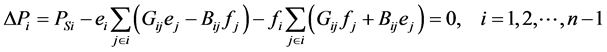


定义 =
当前迭代点,
=
当前迭代点, = 上次迭代点,
= 上次迭代点,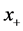 = 下次迭代点,
= 下次迭代点, 为当前雅克比矩阵
为当前雅克比矩阵 ,定义
,定义 为修正向量,即
为修正向量,即 。在计算中,取
。在计算中,取 ,则在(3)中,
,则在(3)中,
 ,
, .
.
最终我们可以使用张量法建立潮流修正方程,即:
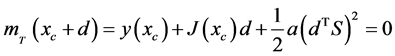 (4)
(4)
接下来,本文将论述如何计算式(4)的根,即:寻找 ,满足
,满足

如果方程没有解,将求出其最小二乘意义下的解。为了有效的求解(4)式,我们可以用两次正交变换将(4)式转换为含 个未知量的
个未知量的 个方程
个方程
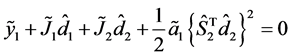 (5)
(5)
和含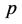 个未知量的
个未知量的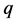 个方程
个方程
 (6)
(6)
可以通过求(6)式最小二乘意义下的解得到 ,通过回代(5)式解出
,通过回代(5)式解出 ,从而求出张量模型的解
[7] 。具体算法见流程图1及附录A。
,从而求出张量模型的解
[7] 。具体算法见流程图1及附录A。
将计算出的结果作为初值,继续计算,获得系统的PV曲线。
4. 算例及分析
在本章中,我们将使用IEEE-5, 11, 13节点系统进行张量法与牛顿法潮流计算的对比测试 [8] ,测试结果如下:
4.1. IEEE-5节点系统重负荷下的潮流计算
对于IEEE-5节点系统,同时增加系统的所有的有功和无功负荷到功率极限点,即原始负荷的1.28
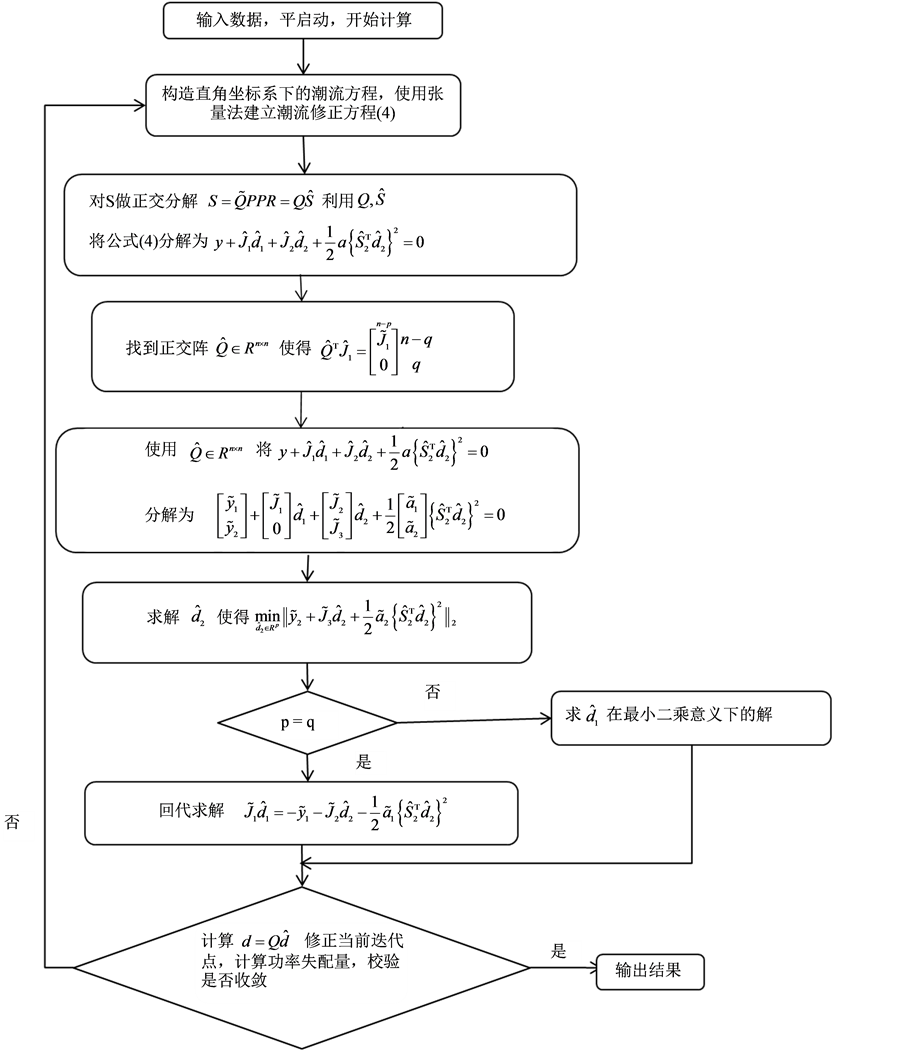
Figure 1. The calculation flow chart of tensor method
图1. 张量法计算流程图
倍 [9] 。使用牛顿法和张量法计算潮流,计算采用平启动,收敛条件为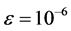 ,结果如表1所示。
,结果如表1所示。
从表1中我们可以看出,在良态系统中,张量法的效率和牛顿法大致相同。
4.2. IEEE-11节点系统
对于IEEE-11节点系统,使用张量法和牛顿法计算潮流,令最大迭代次数为30,收敛条件为 ,计算结果两种方法都不收敛。以迭代次数为X轴,最大误差为Y轴,绘制图2,图3。
,计算结果两种方法都不收敛。以迭代次数为X轴,最大误差为Y轴,绘制图2,图3。
表1. IEEE-5节点重负荷潮流计算结果

Figure 2. The iterative error of IEEE-11 with tensor method
图2. IEEE-11节点系统张量法迭代误差

Figure 3. The iterative error of IEEE-11 with Newton method
图3. IEEE-11节点系统牛顿法迭代误差
由以上两图可以看出,对于在潮流不收敛的时候,张量法可以将误差限制在0.005724以下,而牛顿法的误差振荡,潮流计算发散。可见张量法可以保证潮流不发散。如果把收敛条件改为 ,则张量法收敛,而牛顿法仍然发散。张量法计算的潮流结果见表2。
,则张量法收敛,而牛顿法仍然发散。张量法计算的潮流结果见表2。
4.3. IEEE-13节点系统
4.3.1. 重负荷下的潮流计算
IEEE-13节点系统为一个病态系统 [8] 。将系统中所有节点的负荷有功和无功增加到10倍的初始负荷,使用张量法和牛顿法计算潮流,平启动,收敛条件为 ,结果见表3。
,结果见表3。
由表3知,对于IEEE-13节点系统,在重负荷时,张量法计算潮流仍然收敛,而牛顿法计算结果发散,误差振荡。可见,在病态潮流计算中,张量法比牛顿法稳定,可靠。
4.3.2. 绘制PV曲线
以1为步长,只增加IEEE-13节点系统所有负荷的有功,使用张量法和牛顿法绘制PV曲线。以负荷为X轴,10号节点电压为Y轴,使用上次计算的值作为下次迭代的初值进行计算,每次迭代收敛条件为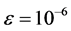 ,结果见图4、图5。
,结果见图4、图5。
表2. IEEE-11节点潮流计算结果
表3. IEEE-13节点系统重负荷下潮流计算结果

Figure 4. The PV-curve of IEEE-13 system with tensor method
图4. IEEE-13节点系统张量法计算PV曲线
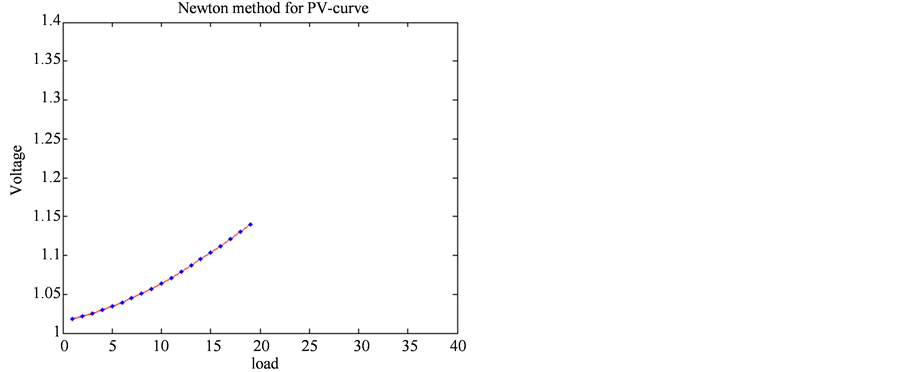
Figure 5. The PV-curve of IEEE-13 system with Newton method
图5. IEEE-13节点系统牛顿法计算PV曲线
由图4、图5中知,当系统有功负荷达到19倍的初始负荷,如果继续增大负荷,牛顿法将发散,但张量法在达到38倍的额定负荷时依然收敛。这又一次证明了再计算病态潮流问题时,张量法的可靠性高于牛顿法。
5. 结论
由以上结果我们可以得出以下结论:
1) 对于良态的潮流问题,张量法的运算效率和可靠性与牛顿法大致相同。
2) 对于病态潮流问题,张量法的可靠性远高于牛顿法。
3) 对于不收敛的潮流问题,张量法能够保证潮流计算的不发散。
4) 由于使用内插 个已求点来拟合张量模型
个已求点来拟合张量模型 ,使得张量法所需要的存储空间和计算量同牛顿法相比并无太大的增加,因而张量法是一种比较实用的病态潮流计算方法。
,使得张量法所需要的存储空间和计算量同牛顿法相比并无太大的增加,因而张量法是一种比较实用的病态潮流计算方法。
5) 在绘制PV曲线的过程中,张量法比牛顿法具有更高的可靠性
因此,张量法适合求解电力系统病态潮流与绘制系统PV曲线。
文章引用
姜 山,杜一盟, (2015) 基于张量法的电力系统病态潮流求解与PV曲线绘制
Solution of Ill-Conditioned Load Flow for Power System and the Drawing of PV-Curve
Based on Tensor Method. 电力与能源进展,04,69-78. doi: 10.12677/AEPE.2015.34011
附录A:张量法求解详细推导过程
1) 做正交分解 ,取置换阵
,取置换阵

则 ,
, 是
是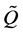 的列的置换,
的列的置换, 是
是 的行的置换。
的行的置换。
2) 计算 ,
, ,
,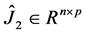 ;定义
;定义 ,
,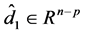 ,
, ,则
,则
 (A-1)
(A-1)
3) 找到正交阵 ,使得
,使得

式中 为对角元素非零的上三角阵。由于
为对角元素非零的上三角阵。由于 可能是列亏秩的,因而
可能是列亏秩的,因而 。
。
4) 计算
 ,
, ,
, ,则(A-1)式可变为:
,则(A-1)式可变为:
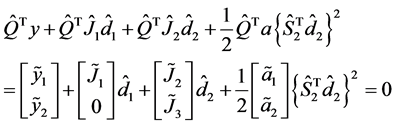
5) 在最小二乘意义下求解:
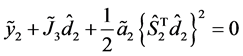
找到 ,即
,即

6) 当 时,回代求解,即求解
时,回代求解,即求解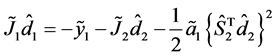
得到 。当
。当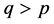 时,需要求
时,需要求 在最小二乘意义下的解。
在最小二乘意义下的解。
7) 计算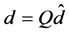 ,得到
,得到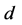 。
。
当计算出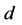 后,可以修正当前迭代点
后,可以修正当前迭代点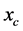 ,即
,即 ,得到下一个迭代点
,得到下一个迭代点 。计算功率失配量,
。计算功率失配量,
如果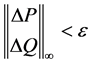 ,则停止计算,否则,重复计算直到收敛。
,则停止计算,否则,重复计算直到收敛。
参考文献 (References)
- 1. 夏道止 (2004) 电力系统分析. 中国电力出版社, 北京.
- 2. 李渊 (2009) 现代电力系统病态潮流算法的研究. 华电技术, 5, 24-27.
- 3. Iwamoto, S. and Tamura, Y. (1986) A load flow calculation method for ill-conditioned power systems. IEEE Transactions on Power Apparatus and Systems, 100, 1736-1743.
- 4. Sasson, A.M. (1971) Improved Newton’s load flow through a minimization technique. IEEE Transactions on Power Apparatus and Systems, 90, 1974-1981.
- 5. Schnabel, A.B.R. (1994) TENSOLVE—A software package for solving systems of nonlinear equations and nonlinear least squares problems using Tensor methods. CRPC-TR94586 August 1994.
- 6. 王绵森, 马知恩 (1998) 工科数学分析基础(上). 高等教育出版社, 北京, 8.
- 7. Schnabel, R.B. and Frank, P.D. (1983) Tensor methods for nonlinear equations. Department of Computer Science University of Colorado Boulder, Colorado 80309. Cu-Cs-243-83 April, 1983.
- 8. Tripathy, S.C., Prasad, G.D., Malik, O.P. and Hope, G.S. (1982) Load-flow solutions for ill-conditioned power systems by a newton-like method. IEEE Transactions on Power Apparatus and Systems, PAS-101, 3648-3657. http://dx.doi.org/10.1109/TPAS.1982.317050
- 9. 蔡晔, 徐政 (2002) 基于PSS/E 的节点静态电压稳定极限计算. 华东电力, 9, 27-29.
