Advances in Energy and Power Engineering
Vol.
07
No.
02
(
2019
), Article ID:
29270
,
9
pages
10.12677/AEPE.2019.72003
Lattice Boltzmann Simulation of Flow and Heat Transfer in Porous Media
Wei Tian, Zhichun Liu, Wei Liu
School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan Hubei

Received: Feb. 21st, 2019; accepted: Mar. 8th, 2019; published: Mar. 15th, 2019

ABSTRACT
In this paper, a digital model of porous media is obtained by four-parameter stochastic generation method. And an improved lattice Boltzmann method is used to simulate the flow and heat transfer problems in this porous media. The distribution of velocity and temperature is obtained at different porosity. On the basis of the results, the effective thermal conductivity of porous media is calculated. And the value is affected by the flow state in porous media. A reliable simulation method for study flow and heat transfer in porous media can be obtained in this paper.
Keywords:Porous Media, Lattice Boltzmann Method, Heat Transfer, Flow
LBM方法模拟多孔介质流动与传热问题
田巍,刘志春,刘伟
华中科技大学能源与动力工程学院,湖北 武汉

收稿日期:2019年2月21日;录用日期:2019年3月8日;发布日期:2019年3月15日

摘 要
多孔介质在诸多领域有着广泛应用,了解其特性具有重要意义。为对多孔介质中相关流动与传热特性进行研究。本文通过四参数随机生成法获得多孔介质数字模型,在此基础上利用改进的格子Boltzmann方法对多孔介质内部的流动与传热问题进行了数值模拟。得到了不同孔隙条件下,多孔介质内部温度场、速度场以及有效导热系数。结果显示,在内部流体工质流动状态下,多孔介质导热系数会受到流体流动影响,有所提高。本文为多孔介质相关流动与传热特性提供了一种可靠的模拟方法。
关键词 :多孔介质,格子Boltzmann方法,传热,流动

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在油藏开采、化学化工、航天航空、地质科学及生命科学等诸多领域,都有着多孔介质的存在或应用。因此对于多孔介质动量、质量和能量等方面的基础研究工作具有重要的意义。传热传质与流动现象经常涉及从宏观到微观多个尺度范围,尺度相差可以达到20个数量级,这种涉及到多个尺度的物理问题,我们将其统称为多尺度问题。多孔介质的流动与传热问题就是一种多尺度问题。因此,为了更准确地观察了解多孔介质内部流动与传热规律,必需从多个尺度对多孔介质进行研究。
对于多孔介质的数值模拟工作,已有学者从不同的尺度和研究方法做出了成果。但是我们可以发现,通常的研究工作多是从宏观尺度展开,求解纳维–斯托克斯方程组。这种研究方式具有很大的局限性,难以捕捉大量微小、分散的界面,无法了解多孔介质内部具体的流动传热现象。因此,一种更小尺度的数值模拟方法显得十分必要。
格子Boltzmann方法是一种基于分子动理学的介观研究方法,能够很好地描述多孔介质内部复杂、细小的界面。由于格子Boltzmann方法的介观特性,以及边界条件处理简单、计算效率高、可并行计算、代码简单易行的优点,被广泛应用于多孔介质等具有复杂界面结构对象的小尺度数值模拟工作中 [1] [2] 。在此基础上,Guo等人对多孔介质中的流动问题做了大量的工作 [3] ,Wang等人 [4] 对多孔介质结构的有效导热系数进行了相关研究。现有的研究工作多是对多孔介质的流动或者导热问题进行研究 [5] [6] 。但是,实际应用中,往往需要分析内部伴随流体流动的多孔介质传热传质过程。因此,本文采用格子Boltzmann方法,结合四参数随机生成法(QSGS)生成具有内部随机结构的多孔介质,对多孔介质内部传热与流动现象做了模拟研究工作,并计算了相应条件下的有效导热系数,为多孔介质内部流动与传热现象的介观研究提供了一种可行的思路。
2. 计算模型
2.1. 四参数随机生成方法(QSGS)
本文采用Wang等人 [7] 提出的四参数随机生成方法,通过控制四个参数的大小,随机生成多孔介质的内部结构,获得具有内部随机结构的多孔介质数字模型。并根据应用条件,对这种方法做了相应改进,使其更好适应本文研究内容。具体的生成方法如下:
1) 根据生长核分布概率密度数,在计算区域中选取随机格点作为生长相的生长核,该概率数小于固体骨架体积分数。
2) 根据生长概率密度数,令固体骨架由生长核向四周生长。
3) 重复步骤2,直到当固体骨架体积分数达到给定值时,停止生长。
4) 最后未被生长相占据的空间代表了孔隙空间。
通过QSGS方法我们可以获得随机多孔介质数字模型,这类多孔介质内部边界通过随机数生成,具有与实际相似的随机结构特征。
2.2. 格子boltzmann模型
本文对于多孔介质内部流动与传热现象格子Boltzmann模拟选用了Guo等人提出的基于Boussinesq假设的耦合双分布函数模型 [8] [9] 。并进行了相应的改进工作,对密度和温度分布函数的计算均采用D2Q9的速度离散格式。相应的分布函数演化方程可以表示为如下形式:
(1)
(2)
其中δt为时间步长,ei为格子离散速度。τf为密度分布计算的弛豫时间,τg为温度密度函数计算的弛豫时间。宏观温度、热流密度可通过以下公式获得:
(3)
(4)
其中ρcp为相应的物性参数,τT为温度分布弛豫时间,δt为时间步长。同时在得到稳态条件下热流密度的情况下,根据傅里叶导热定律,可以获得有效导热系数的计算公式:
(5)
其中δ为导热方向的距离,∆T为定温条件下导热方向壁面温差,A为垂直于导热方向的面积。
2.3. 边界条件
根据研究经验,在保证计算准确的条件下,为提高计算效率,本文选用200 × 200的格点区域进行计算,其中空间步长δx = 1,时间步长δt = 1,密度分布函数计算弛豫时间τf = 1.5,计算边界条件上下边界为绝热壁面边界条件,保证边界速度及边界热流密度为零,采用反弹边界条件格式,出口边界选择非平衡态外推格式。入口边界根据计算条件需求,流体密度边界设置为恒定速度边界,温度边界设置为定温边界或定热流边界条件。
对于多孔介质内部不同组分之间的作用处理方式是模拟的研究重点。在流动过程中固体骨架内部不参与流动,密度分布函数分布为零,流固作用的界面采用相应的反弹格式,使固相边界能够在计算过程中落在格点中间位置。传热过程中,本文选用局部热平衡模型,界面处不同相之间温度与热流密度相同,如下所示:
 (6)
(6)
 (7)
(7)
同时温度分布函数计算时,流固界面处选用耦合弛豫时间,保证在计算过程中演化方程的一致性 [7] 。
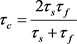 (8)
(8)
2.4. 模型验证
通过对不同材料串联模型的传热模拟计算,我们验证了所选数值模型以及相应计算公式的准确性。根据理论分析我们可以知道,在串联条件之下,如图1,温度分布可以通过下列公式计算:
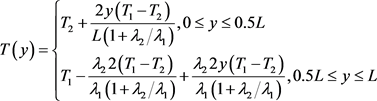 (9)
(9)

Figure 1. Series models
图1. 串联模型
在模型验证中,两种不同物质导热系数比值被设定为1:10,1:100,1:1000,并选用了与前文相同的格子Boltzmann模型与边界格式。通过图2结果我们可以发现数值模拟温度分布结果与理论分析结果具有良好的一致性,我们可以认为所采用的模型及相关的边界条件是准确可靠的。

Figure 2. Temperature distribution of series models
图2. 串联模型温度分布
3. 结果与讨论
3.1. 多孔介质传热数值计算
3.1.1. 随机多孔介质构建
为了对多孔介质相关性质进行研究,我们首先利用QSGS法构建了具有内部随机结构的多孔介质数字模型。获得结果如图3所示。
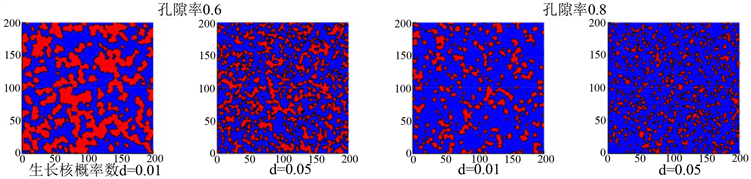
Figure 3. Digital porous media generated by QSGS
图3. QSGS法生成多孔介质
在之后的模拟计算过程中发现原始QSGS方法构建的随机多孔介质在较小孔隙率条件下,内部往往会出现被固相包围的孔隙区域,减小多孔介质整体的有效孔隙率。为保证在较低孔隙率下的模拟效果,我们对原始的QSGS方法做了调整,将初始生长相由固相骨架更改为孔隙区域,增大了多孔介质模型的有效孔隙率。改进后的模型如下图4所示。
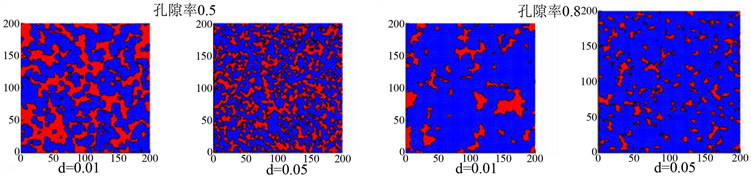
Figure 4. Digital porous media generated by improved QSGS
图4. 改进QSGS方法生成多孔介质
3.1.2. 多孔介质传热流动过程数值计算
获取随机多孔介质以后,我们利用改进的D2Q9耦合双分布函数模型,对多孔介质内部孔隙空间有流体工质流动的条件下,其流动与传热问题进行了数值模拟分析。研究对象是孔隙率为0.8的多孔介质,左边入口边界分别采用了2.225e-3 lu (lu为格子单位)定热流边界条件与310 K定温边界条件,右边出口边界为300 K定温边界。其他边界条件与前文相同,骨架与流体之间温度分布函数计算采用耦合弛豫时间,数值计算结果如下图5、图6及图7所示。
通过对定温边界与定热流边界条件的具体分析,可以获知,在定热流条件下达到稳态后,形成了稳定的温度梯度,与定温情况相似。定热流条件下,多孔介质两端温差为10.487 K,有效导热系数为2.883 W/m∙K。定温条件下,多孔介质两端温差为10 K,有效导热系数为2.888 W/m∙K。两者计算结果之间相对误差为0.17%,进一步验证了计算模型的可靠性。
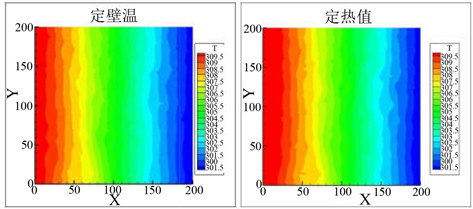
Figure 5. Temperature distribution in porous media
图5. 温度场分布

Figure 6. Temperature of central at different boundary
图6. 不同壁面条件中心高度

Figure 7. Velocity distribution in porous media
图7. 速度场分布
3.2. 多孔介质有效导热系数计算
完成对多孔介质内部流动传热过程的数值模拟之后,我们利用该模型对不同孔隙率条件下的随机多孔介质有效导热系数进行了分析计算。其中相应的计算条件为,进出口边界为等温边界条件,高温壁面310 K,低温壁面为300 K,流体流动方向与热量传递方向相同。本文研究分别选取了孔隙率为0.6、0.7、0.75、0.8、0.85、0.9的随机多孔介质进行了有效导热系数计算,并将计算结果同相应经验公式 [10] 进行了对比,结果如下图8所示。

Figure 8. Effective thermal conductivity of porous media at different porosity
图8. 不同孔隙率多孔介质有效导热系数
我们可以发现数值模拟计算的多孔介质有效导热系数随着孔隙率地增加而逐渐降低,这种变化趋势与经验公式相吻合,这是由于固相骨架的热导率明显高于流体介质,在传热过程中占据了主导地位。同时我们可以发现经验公式有效导热系数降低同孔隙率呈线性关系,但是模拟计算值有效导热系数降低幅度在逐渐减小。我们分析认为这是因为经验公式主要应用于多孔毛细芯等低流速场景,没能充分考虑流体介质流动对传热产生的影响。我们猜想在高孔隙率条件下,流体工质在多孔介质内的流动变得剧烈,对整个传热过程的影响变得不可忽略,这也正是本文研究同已有研究的不同点。为了验证这个猜想,我们对高孔隙率条件下的多孔介质进行了进一步的模拟研究。获得了相应的有效导热系数和速度场,并同之前模拟结果进行了比较。结果如下表1所示。
Table 1. Effective thermal conductivity of porous media at different porosity
表1. 不同孔隙率多孔介质有效导热系数
通过表我们可以发现随着多孔介质孔隙率的进一步增加,随机多孔介质的有效导热系数不在继续下降,保持在2.6 W/m∙K附近,并有升高的趋势。其内部流动状况如下图速度场图9所示。

Figure 9. Velocity distribution in porous media at different porosity
图9. 不同孔隙率多孔介质内部流场图
通过高孔隙率条件下多孔介质内部流场图,我们可以清晰发现在孔隙率0.9以上时,多孔介质内部流动明显较低孔隙率情况下(孔隙率0.8以下)更为强烈,此时流体介质的流动对整个多孔介质传热特性的影响不容忽视,流体的强烈的对流效应对多孔介质传热性能强化作用削弱了由于固体骨架体积分数减小的影响,提高了多孔介质整体的有效导热系数。
4. 结论
通过四参数随机生成方法我们获得了具有内部随机结构的多孔介质数值模型。在此基础上我们将D2Q9离散格式应用于格子Boltzmann双分布函数模型,并对流固界面的传热问题进行了耦合求解,得到了以下结果:
1) 本文采用的改进多孔介质LBM模拟方法可以有效地对多孔介质内部的流动与传热问题进行模拟研究,通过与理论分析解的对比,该计算方法在变化趋势及数值精度上都具有较好的可靠性。
2) 通过进一步应用这种计算模型分析了不同孔隙率条件下的多孔介质流动传热现象,发现了在高孔隙率条件下,多孔介质有效导热系数会受到内部流体工质流动的影响,相对于静止状态有所提高。通过对比分析经验关联式对多孔介质有效导热系数的计算结果,本文采用的计算方法能更好地预测多孔介质有效导热系数随孔隙率的变化情况。
基金项目
本研究受国家自然科学基金面上项目(NO. 51776079)资助。
文章引用
田 巍,刘志春,刘 伟. LBM方法模拟多孔介质流动与传热问题
Lattice Boltzmann Simulation of Flow and Heat Transfer in Porous Media[J]. 电力与能源进展, 2019, 07(02): 23-31. https://doi.org/10.12677/AEPE.2019.72003
参考文献
- 1. Zhou, P., Liu, W. and Liu, Z. (2019) Lattice Boltzmann Simulation of Nucleate Boiling in Micro-Pillar Structured Surface. International Journal of Heat and Mass Transfer, 131, 1-10. https://doi.org/10.1016/j.ijheatmasstransfer.2018.11.038
- 2. Zhou, P., Ma, L., Liu, W., et al. (2018) Study on Thermal Con-ductivities of Si Thin Films and Porous Si Structures Based on a Modified Lattice Boltzmann Method. Journal of Applied Physics, 124, Article ID: 104302. https://doi.org/10.1063/1.5040127
- 3. Guo, Z.-L. and Zhao, T.-S. (2002) Lattice Boltzmann Model for Incompressible Flows through Porous Media. Physical Review E, 66, Article ID: 036304. https://doi.org/10.1103/PhysRevE.66.036304
- 4. Wang, M.-R., Wang, J.-K., Pan, N., et al. (2007) Mesoscopic Predictions of the Effective Thermal Conductivity for Microscale Random Porous Media. Physical Review E, 75, Article ID: 036702. https://doi.org/10.1103/PhysRevE.75.036702
- 5. Wang, M.-R., He, J.-H., Yu, J.-Y., et al. (2007) Lattice Boltzmann Modeling of the Effective Thermal Conductivity for Fibrous Materials. International Journal of Thermal Sciences, 46, 848-855. https://doi.org/10.1016/j.ijthermalsci.2006.11.006
- 6. Xu, R.-N. and Jiang, P.-X. (2008) Numerical Simulation of Fluid Flow in Microporous Media. International Journal of Heat and Fluid Flow, 29, 1447-1455. https://doi.org/10.1016/j.ijheatfluidflow.2008.05.005
- 7. Guo, Z.-L., Shi, B.-C. and Zheng, C.-G. (2002) A Coupled Lattice BGK Model for the Boussinesq Equations. International Journal for Numerical Methods in Fluids, 39, 325-342. https://doi.org/10.1002/fld.337
- 8. He, X.-Y., Chen, S.-Y. and Doolen Gary, D. (1998) A Novel Thermal Model for the Lattice Boltzmann Method in Incompressible Limit. Journal of Computational Physics, 146, 282-300. https://doi.org/10.1006/jcph.1998.6057
- 9. Wang, D.-D., Liu, Z.-C., Shen, J., et al. (2015) Lattice Boltzmann Simulation of Effective Thermal Conductivity of Porous Media with Multiphase. Journal of Porous Media, 18, 929-939. https://doi.org/10.1615/JPorMedia.2015012117
- 10. Hanlon, M. and Ma, H. (2003) Evaporation Heat Transfer in Sintered Porous Media. Journal of Heat Transfer, 125, 644-652.
