Open Journal of Circuits and Systems
Vol.05 No.04(2016), Article ID:19200,9
pages
10.12677/OJCS.2016.54007
Low-Area and Low-Power Circuit Implementation of Color Space Conversion between RGB and YCbCr
Fei Lu1, Hu Cao2
1Shanghai IC Technology Industry Promotion Center, Shanghai
2Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai

Received: Nov. 21st, 2016; accepted: Dec. 9th, 2016; published: Dec. 13th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper presents a low-area and low-power circuit implementation of high-precision color space conversion from RGB to YCbCr. Firstly, an efficient circuit implementation combining common-subexpression-elimination (CSE) with reduced-adder-graph (RAG) is presented. Secondly, a compensation method is proposed to enhance the precision. Finally, the synthesized results of a TSMC 0.18 um standard cell library are given. By using the proposed circuit implementation of color space conversion from RGB to YCbCr combining CSE and RAG without compensation, the results show that the area and power are reduced by about 20% than the traditional Canonic Signed Digital (CSD) method. With the compensation algorithm, the precision is much higher.
Keywords:RGB, YCbCr, Common-Subexpression-Elimination (CSE), Reduced-Adder-Graph (RAG), Compensation

一种低面积低功耗RGB到YCbCr色彩空间转换电路实现方法
陆斐1,曹虎2
1上海集成电路技术与产业促进中心,上海
2中国科学院上海高等研究院,上海

收稿日期:2016年11月21日;录用日期:2016年12月9日;发布日期:2016年12月13日

摘 要
本文提出了一种低面积低功耗RGB与YCbCr色彩空间转换的电路实现方法。首先提出一种结合简化加法器图(Reduced Adder Graph, RAG)的公共子表达式消除(Common Subexpression Elimination, CSE)的电路实现,然后提出一个提高精度的补偿方法。最后采用TSMC 0.18um工艺对所提出的算法进行综合和布局布线。仿真和综合结果表明相比于传统的正则有符号数字(Canonic Signed Digit, CSD)编码系统,采用本文提出的结合CSE和RAG的RGB到YCbCr空间转换电路实现方法面积和功耗减小了20%,补偿算法提高了系统精度。
关键词 :RGB,YCbCr,公共子表达式消除(CSE),简化加法器图(RAG),补偿

1. 引言
随着移动互联网的发展,视频播放器和智能手机等移动多媒体设备已经成为市场上的主流产品。低面积和低功耗是影响专用集成电路(Application Specific Integrated Circuits, ASICs)性能的关键因素,低面积可减小成本而低功耗直接增加电池寿命。对显示设备来说,RGB [1] 是最主流的颜色空间。但是分离的R、G、B无法直接展现色调、饱和度以及亮度等信息,往往不适合各种视频应用场合。而YcbCr [2] 作为RGB的线性转换空间,为大部分显示器所采用,其中Y代表亮度,CbCr分别代表蓝偏和红偏分量。因此研究RGB到YCbCr颜色空间转换的硬件电路实现是很有必要的,这也是多常数乘法器(Multiple constant Multiplication, MCM) [3] 的一个研究问题。
乘法器可以分解为加法器、减法器、移位寄存器来实现。减法器和加法器具有相似的实现复杂度,在本文都称作加法器。单常数乘法问题的优化对编译器和综合工具都是至关重要的,应用CSD [4] 编码方式可以有效降低乘法电路面积,因为CSD编码的非零元素是最少的。在一个n位CSD数中非零位的数量近似为n/3 + 1/9。例如,为了实现乘法器运算{D = 13A + 59B + 75C},转换各个系数的二进制编码为{13:1101, 59:111011, 75:1001011},传统的移位相加运算方法是分别实现A,B,C的乘法系数再相加{D = A<<3 + A<<2 + A + B<<5 + B<<4 + B<<3 + B<<1 + B + C<<6 + C<<3 + C<<1 + C},需要九个移位寄存器和11个加法器。CSD编码优化后为{D = A<<3 + A<<2 + A + B<<6 − B<<2 − B + C<<6 + C<<3 + C<<1 + C},需要7个移位寄存器和9个加法器,比传统的二进制编码节约了2个加法器和2个移位寄存器。
CSE [5] 算法和基于图(Graph-dependence, GD)的算法是更为高效的算法,CSE算法的思想是找到系数集的公共子表达式,为实现上文的乘法器运算,令{E = A − B},那么表达式变成{D = A<<3 + E<<2 + E + B<<6 + C<<6 + C<<3 + C<<1 + C},需要6个移位寄存器和8个加法器,比CSD编码方式节省了1个移位寄存器和1个加法器。而GD算法中的n维简化加法器图(n-dimensional reduced adder graph, RAG-n) [6] [7] 算法用最少的加法器数量产生乘法器。例如为了实现乘法器集合{F1 = 13A; F2 = 59A; F3 = 75A},基于CSD编码的一般方法表示为{13A = A<<3 + A<<2 + A},{59A = A<<6 − A<<2 − A}和{75A = A<<6 + A<<3 + A<<1 + A},需要四个移位寄存器和7个加法器。2005年改进的算法RAG-05选择将中项{15A = A<<4 − A}表示为{13A = 15A − A<<1},{59A = (15A)<<2 − A}和{75A = (15A)<<2 + 15A},只需要3个移位寄存器和4个加法器,相比CSD编码方式节省了1个移位寄存器和3个加法器。RAG算法虽然高效,但找到最优解却非常困难,尤其系数比较大的时候。
2. 改进方法
本节提出了一种有效的RGB到YCbCr颜色空间转换的低面积低功耗电路实现方法,同时提出了一个提高精度的补偿方法。
2.1. RGB到YCbCr的颜色空间转换
在视频处理中,YCbCr是最常使用的颜色空间之一。Y代表亮度,Cb、Cr分别代表蓝偏和红偏分量,YCbCr颜色空间与视觉属性更紧密的联系使YCbCr比RGB更便于运用到影像处理中。
YCbCr与RGB之间的转换公式 [8] 定位为:
 (1)
(1)
首先,需要实现的浮点运算被转化成乘法和移位。一般采用的策略是将浮点系数乘以2^n,然后取整,最后将结果又移n位(n为精度宽度)。对于精确度的判断标准一般是均方误差MSE (Mean Square Error) [9] 。均方误差代表数据整体均值的偏移量,常常用于判断统计数据的误差率。MSE的定义如下:
 (2)
(2)
其中S是像素的个数,p是浮点运算得到的Y,Cb,Cr的精确值,p’是浮点系数乘以2^n,取整右移n位实现的近似值。MSE与n的关系如图1所示,可以看到当n增大的时候精确度增加。
假设R,G,B,Y,Cb,Cr为8位二进制数,n取12,那么RGB到YCbCr的空间转换操作如下:
 (3)
(3)
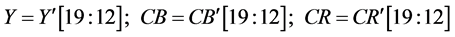 (4)
(4)
2.2. 寻找显著的公共子表达式
CSD编码具有最小数量的1(-1),因此,第一步是把所有系数转换成CSD编码格式。文献 [10] 主要考虑输入信号的组合,然后尝试找到一种使用最少加法器数量的方法。对于一个乘法器集,加法器的数量减少大概50%。虽然有研究尝试找出最优公共子表达式,但是当系数很大的时候是很难找出最优公共子表达式的。在本文提出的算法中,只需要找出显著的公共子表达式。
如图2所示有三个显著的子表达式,定义如下:
 (5)
(5)
2.3. RAG-05算法
加法器图的概念是Bull和Horrocks提出的,Bull和Horrocks [6] 在1995年发表了在FIR数字滤波器中运用的最少加法器的乘法器模块,称为RAG-95。其算法流程如下:
(i) 将输入集合中的所有系数简化为正奇基数,将结果保存到输入集;
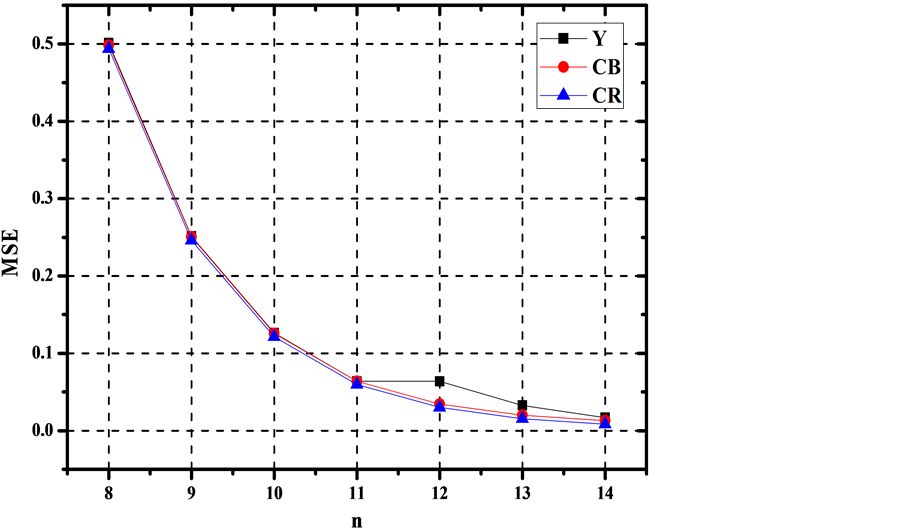
Figure 1. Relationship between MSE and n
图1. MSE与n的关系

Figure 2. CSD coding and common sub expressions of coefficients
图2. 系数的CSD编码及公共子表达式
(ii) 利用MAG表来计算所有系数的单系数的加法器成本;
(iii) 删除输入集合中所有2的幂的值和重复的基数;
(iv) 创建能用一个用加法器构造的所有系数图集,然后从输入集合中删除这些满足条件的系数;
(v) 检查图集中是否有一对基数用一个加法器在输入集合生成一个系数;
(vi) 重复步骤v,知道没有系数添加到图集中为止。
相比于RAG-95,2005年发表的RAG-05 [7] 已经有了一些改进。首先使用的MAGLUT表已经扩展到14位,并且当计算最小NOF累加和时,考虑所有32MAG加法器成本为4的图。然后考虑所有加法器成本为2的图,最后的改进基于加法器成本为2的选项,当必须实现多个加法器成本为2的系数时,在RAG-95算法中通常生成次最优结果。例如对于乘法器集{F1 = 13A; F2 = 59A; F3 = 479A},RAG-95所用的最小NOF值为{3; 5; 7},因为{13 = 4 × 3 − 1; 59 = 64 − 5; 479 = 59 × 8 + 7},结果是6加法器组成的一幅图。在RAG-05中,选择NOF {15},那么所有系数{13A = 15A − A<<1; 59A = (15A)<<2 − A; 479 = (15A)<<5 − A}只需要4个加法器。所以,除了为最小加法器成本为2的系数选择最小NOF,可以为所有与加法器成本为2的系数寻找最佳NOF。
本文把RAG-05算法运用到R,G,B和所有公共子表达式,最佳结果如表1所示。
2.4. 提高精度的补偿方法
如上所述,浮点系数乘以2^n,然后取整不可避免地损失了精度。例如n = 8,Y’的精确表达式和近似表达式分别为{76.544R + 150.272G + 29.184B}和{76R + 150G + 29B},可以看出损失了{0.544R + 0.272G + 0.184B}。因为{R[7]≈R/128; R[7:6]≈R/64; R[7:5]≈R/32; R[7:4]≈R/16; R[7:3]≈R/8; R[7:2]≈R/4; R[7:1]≈R/2},G和B具有相同的性质,上文中的一些表达式可以被选择来作为损失精度的补偿。然而过多的加法器会导致过高的面积和功耗。因此每项的表达式被限制为2个加数和1个加法器,补偿的近似表达式如下:
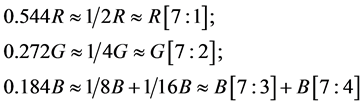 (6)
(6)
对Cb和Cr采用相同的补偿方法,没有补偿的均方误差MSEs (n = 10/11/12/13/14)和n = 8时有补偿的均方误差如图3所示。可以看到n = 8时带补偿的均方误差明显低于n = 12时不带补偿的均方误差,证明了所提出的补偿方法是有效的。
Table 1. Realization of coefficients based on RAG-05 algorithm
表1. 基于RAG-05算法的系数实现

Figure 3. Original color space conversion MSE and MSE with compensation
图3. 原始的颜色空间转换MSE和带补偿的MSE
2.5. 专用电路实现
带补偿方法的电路实现流程图如图4所示,Y/Cr/Cb的值就可以由联合RAG-05和CSE算法的取整电路和补偿电路以及移位寄存器组成的电路求得。
3. 实验结果
在TSMC 0.18 um工艺下,采用DC工具对本文所提出的结合CSE和RAG-05算法和带补偿的色彩空间转换电路进行综合验证。电路输入和输出数据为8位,为了更有效地对比面积和功耗的优化,时钟约束到250 MHz。综合所得到的面积和功耗如下。
3.1. 联合CSE和RAG-05不带补偿下的实验结果
精度宽度的值为12,用二进制编码、CSD编码、RAG算法、CSE算法和不带补偿的结合CSE和RAG的算法分别实现电路所需的加法器数量如表2所示,面积和功耗对应的综合结果如图5所示,结果表示所提算法比传统的方法明显节约了加法器的数量。
基于CSD编码和不带补偿的结合CSE和RAG的算法的面积与功耗如图6所示,从图7可以看出面积与功耗减少了大约20%。
3.2. 补偿方法的实验结果
n值设为8,每一项的补偿限制为两个加数和一个加法器,原始的颜色空间转换如下所示:
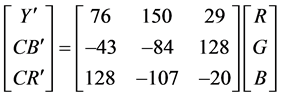 (7)
(7)
补偿部分的实现如下所示:
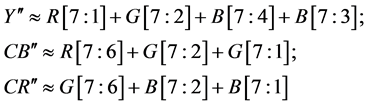 (8)
(8)
合并结果如下:

Figure 4. Flow chart of color space conversion from RGB with compensation to YCbCr
图4. 带补偿的RGB到YCbCr颜色空间转换流程图
Table 2. The traditional method and the proposed algorithm circuit to achieve the required number of adder
表2. 传统方法和所提算法电路实现所需加法器数量

Figure 5. The comprehensive results of the area and power consumption of binary coding, CSD, RAG, CSE, and the proposed algorithm
图5. 二进制编码、CSD、RAG、CSE、所提算法的面积与功耗综合结果

Figure 6. The area and power consumption of the proposed algorithm with CSD coding and without compensation
图6. CSD编码和不带补偿的所提算法的面积与功耗

Figure 7. The area and power consumption of the proposed algorithm with CSD coding
图7. 基于CSD编码和所提算法的面积与功耗
Table 3. Results with/without compensation
表3. 带/不带补偿结果
 (9)
(9)
n = 12不带补偿的综合结果和n = 8带补偿的综合结果如表3所示,可以看到带补偿的精度大幅度提高。虽然加法器的数量增加了,但是不带补偿的Y’/CB’/CR’为20位而带补偿的Y’ + Y’’/CB’ + CB’’/CR’ + CR’’只有16位。更重要的是,补偿部分使用非常简单的加法器,使得带补偿的电路面积和功耗甚至更为低一些。
4. 结论
传统的CSE和RAG-05虽然有效,但是仍然难以求取最优解。本文提出了一种RGB与YCbCr颜色空间转换的高精度低面积低功耗电路实现方法,结合CSE和RAG-05实现低面积低功耗电路,并提出了提高精度的补偿方法,综合结果表明带补偿的电路实现精度明显优于不带补偿的电路。
基金项目
上海市科学委员会资助项目(14511102300)。
文章引用
陆 斐,曹 虎. 一种低面积低功耗RGB到YCbCr色彩空间转换电路实现方法
Low-Area and Low-Power Circuit Implementation of Color Space Conversion between RGB and YCbCr[J]. 电路与系统, 2016, 05(04): 51-59. http://dx.doi.org/10.12677/OJCS.2016.54007
参考文献 (References)
- 1. ElDahshan, K.A., Yourself, M.I., Masameer, E.H. and Hassan, M.A. (2015) Comparison of Segmentation Framework on Digital Microscope Images for Acute Lymphoblastic Leukemia Diagnosis Using RGB and HSV Color Spaces. Journal of Biomedical Engineering and Medical Imaging, 2, 26.
- 2. Naskar, R. and Chakraborty, R.S. (2013) Histo-gram-Bin-Shifting-Based Reversible Watermarking for Colour Images. IET Image Processing, 7, 99. https://doi.org/10.1049/iet-ipr.2012.0232
- 3. Logeshwari, N., Aarthi, B., Manikandan, K., Yogeswari, K., Vishnupriya, M. and Priya, S. (2015) Optimization of Area in Digit Serial Multiple Constant Multiplication at Gate Level. Digital Siginal Processing, 7, 50.
- 4. Kim, S.M., Chung, J.G. and Parhi, K.K. (2003) Low Error Fixed-Width CSD Multiplier with Efficient Sign Extension. IEEE Transactions on Circuits and Systems II, 50, 984. https://doi.org/10.1109/TCSII.2003.820231
- 5. Yao, C.Y., Chen, H.H., Lin, T.F., Chien, C.J. and Hsu, X.T. (2004) A Novel Common-Subexpression-Elimination Method for Synthesizing Fixed-Point FIR Filters. IEEE Transactions on Circuits and Systems I, 51, 2215. https://doi.org/10.1109/TCSI.2004.836853
- 6. Dempster, A.G. and Macleod, M.D. (1995) Use of Minimum-Adder Multiplier Blocks in FIR Digital Filters. IEEE Transactions on Circuits and Systems II, 42, 569. https://doi.org/10.1109/82.466647
- 7. Wang, Y. and Roy, K. (2005) CSDC: A New Complexity Reduction Technique for Multiplierless Implementation of Digital FIR Filters. IEEE Transactions on Circuits and Systems I, 52, 1845. https://doi.org/10.1109/TCSI.2005.852208
- 8. Yang, Y., Peng, Y.H. and Liu, Z.G. (2007) A Fast Algorithm for YCbCr to RGB Conversion. IEEE Transactions on Consumer Electronics, 53, 1490. https://doi.org/10.1109/TCE.2007.4429242
- 9. Wang, Z. and Bovik, A.C. (2002) A Universal Image Quality Index. IEEE Signal Processing Letters, 9, 81. https://doi.org/10.1109/97.995823
- 10. Hartley, R.I. (1996) Subexpression Sharing in Filters Using Canonic Signed Digit Multipliers. IEEE Transactions on Circuits and Systems II, 43, 677. https://doi.org/10.1109/82.539000
