Biophysics
Vol.06 No.03(2018), Article ID:26553,7
pages
10.12677/BIPHY.2018.63004
Modulation of Ion Concentration of Isolate Cell Exposed to the Electric Field of High-Voltage Transmission Line
Xiaodi Zhang, Qing Ma, Yongjun Zhou, Hui Zhang*
College of Physics & Electronic Engineering, Xianyang Normal University, Xianyang Shaanxi
Received: Jul. 26th, 2018; accepted: Aug. 16th, 2018; published: Aug. 23rd, 2018

ABSTRACT
The bio-effect of the high-voltage transmission line is one of the hot issues in the study of biological electromagnetics. In this paper, the single cell model and the calculation of the electric field of the high-voltage transmission line with charge simulation method are given. And based on the Nernst formula and the Boltzmann formula, the relative change rate of the ion concentration on the cell surface and its numerical solution are analyzed. The result shows that the higher of the high-voltage transmission line to ground, the smaller the electric field near by the transmission line. The positions of the maximum value and the minimum of the relative change rate of the ion concentration change with the distance change to the under the transmission line. The high-voltage transmission line will produce the bio-effect.
Keywords:High-Voltage Transmission Line, Electric Field Intensity, Ion Concentration, Cell Membrane
高压输电线路对细胞膜一侧离子浓度影响分析
张小娣,马晴,周永军,张辉*
咸阳师范学院物理与电子工程学院,陕西 咸阳
收稿日期:2018年7月26日;录用日期:2018年8月16日;发布日期:2018年8月23日

摘 要
高压输电线路产生的生物学效应是生物电磁学研究的热点问题之一。本文在建立单细胞模型,给出模拟电荷法求解220 KV同塔双回三相高压输电线路产生电场基础上,基于能斯脱公式和玻尔兹曼公式给出电场作用下的细胞膜一侧离子量相对变化公式,并进行数值分析。结果显示:高压输电线路距离地面高度越高,在地面附近产生的电场强度越小;距离输电线铁塔中垂线距离不同,在细胞膜一侧引起的离子跨膜迁移量的变化最大值、最小值位置也不同。高压输电线路将引起细胞生物学效应。
关键词 :高压输电线,电场强度,离子浓度,细胞膜

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着我国经济的快速发展,高压输变电工程日益向人口密集地区深入,输变电工程产生的电磁场对生物体有没有影响,以及如何影响就日益成为人们的关注的问题之一 [1] 。
作为构成生物体的单元——细胞,目前,电磁场对细胞影响的研究有很多报道。如对神经元细胞,王江等 [2] [3] [4] [5] [6] 研究了直流电场和低频交流电场对神经元膜电位的影响,马军等 [7] 根据电磁感应原理和量纲一致原理,建立了一类可以描述电磁感应和电磁辐射效应的神经元模型,牛中奇 [8] 、张辉 [9] [10] [11] [12] 等也分别基于能斯托公式和玻尔兹曼公式分析了电磁波、脉冲波对细胞膜内外离子浓度的影响。但高压输电线路产生的电磁场对细胞作用进而影响细胞两侧离子浓度变化的研究仍是需要关注的问题。基于此,本文以220 KV同塔双回三相输电线路为例,在建立单细胞模型、给出模拟电荷法求解高压输电线路产生电场方法的基础上,基于能斯脱公式和玻尔兹曼公式给出电场作用下细胞膜一侧离子浓度相对变化公式,并通过数值方法进行求解。
2. 理论模型
高压输电线路产生电磁场,处于该电磁环境下的生物体将与电磁场相互作用。从生物物理学角度看,细胞可看成是电磁场作用的目标体。正常情况下,细胞膜内、外维持有一定的静息电位,形成势垒。当外加电磁场作用于细胞时,在细胞膜上产生附加电压,使势垒发生变化,变化的势垒影响粒子对膜的通透性,从而使膜两侧离子的平衡浓度发生变化,引起细胞生命状态的变化,进而产生生物学效应 [8] [9] [11] 。
2.1. 单细胞模型
本文生物细胞采用如图1模型。其中细胞半径为R,细胞膜厚度为 ,细胞内、外和细胞膜的介电常数和电导率电参数分别为: 、 和 。以球形细胞球心为原点 ,垂直地面方向为 轴,与地面平行且垂直高压输电线传输方向为 轴建立坐标系。假设细胞体积很小,高压输电线路在单细胞膜上每点 产生的电场强度相同,该点电场强度沿x方向、y方向电场强度分量分别为 和 , 点与垂直地面y轴夹角为 。
2.2. 高压输电线产生的电场
高压输电线产生的电场可由模拟电荷法 [13] 计算,其基本思想是将到导线表面连续分布的自由电荷或介质分界面上连续分布的束缚电荷用一组离散化的模拟电荷来等效,然后应用叠加原理将离散的模拟电
荷在空间中产生的电场叠加,可得到原连续分布电荷所产生的空间电场分布。
由模拟电荷法有:
(1)
式中, 是各导线对地电压单列矩阵, 是各导线上等效电荷密度的单列矩阵, 是电位系数组成的矩阵。其中,电位系数 可由下式求得:
, (2)
如图2,式(2)中 为i根导线离地高度, 为i、j导线之间的距离, 从为i、j' (j导线的镜像)导线之间的距离, 为i根导线的半径, 为空气介电常数。

Figure 1. Single cell model
图1. 单细胞模型

Figure 2. Sketch map of calculating potential coefficient
图2. 计算电位系数示意图
由叠加原理,空间任意点 电场强度 分量 、 分别为:
、 (3)
式中:以输电线铁塔中垂线与地面交点为坐标原点,垂直地面方向为y轴,与地面平行且垂直高压输电线传输方向为x轴建立坐标系, , 为i根导线的坐标( ),n为导线数目, 、 分别为导线i及其镜像至计算点的距离。
2.3. 电场对细胞跨膜电位的影响
正常情况下,细胞静息膜电位 形成势垒。高压输电线产生的外加电场,在细胞膜上产生附加电位 ,则使势垒V变为:
(4)
根据能斯托公式和玻尔兹曼公式,静息膜电位引起的细胞膜两侧离子浓度 、 (mol/L)有确定关系为 [8] [14]
(5)
式中, 为考虑外加电磁场与细胞膜中双脂层内带电粒子相互作用而引入的修正因子, 为以电压形式表述的粒子热运动能。
外加电场的作用,使细胞膜一侧的离子浓度变为 :
(6)
则电场作用前、后细胞膜一侧离子浓度相对变化量为:
(7)
其中, , 为外加到细胞膜上的电磁强度。
3. 数值分析与讨论
本部分数值分析高压输电线路产生的电场对细胞膜一侧离子浓度的影响,即讨论式(7)中 值。在式(7)中, 根据墨鱼神经干实测的静态伏安特性拟合曲线 [8] [14] 取值为52 mV。细胞半径取 ,细胞膜厚度 。对细胞作用的外电场,以220 KV哈尔滨热电厂——哈东变送电线路 [1] 提供的数据进行建模,采用同塔双回三相输电线路送电,其中分裂导线取4根,分裂间距取400 mm,上相导线与中相导线、中相导线与下相导线高差均为6.2 m,上相导线距铁塔中垂线的水平距离 4.0 m,中相导线、下相导线分别为5.0 m、4.5 m。为研究问题方便,本文讨论场对通过球心且被xoy平面所截的细胞截平面上离子跨膜迁移量的影响情况,即通过改变下相导线离地高度、以及在地面不同高度处,高压输电线路产生的电场对离子跨细胞膜迁移量变化影响。
3.1. 下相导线离地高度、离地不同高度处高压输电线产生的电场分布
在图3中给出了在上、中和下相导线间距不变,而下相导线距离地面分别为12 m、14 m、16 m时,在与传输线垂直且高于地面1.5 m位置处电场强度距原点不同位处关系图。图示说明:在传输线中心处,即原点0点位置,下相导线距离地面高度越高,则对应电场强度的最大值越小(为12 m、14 m和16 m时,
对应的电场强度分别为4.694 kV/m,3.826 kV/m,3.166 kV/m);距离地面12 m处,在距离中心5 m范围内,电场强度的大小超过4 kV/m,这超过国家高压输电线电磁辐射标准 [1] ;传输线距地面高度不同,但电场强度随距离关系图的形状不变。
为讨论对地不同高度处输电线路产生的电场强度的分布,在图4中给出下相导线距离地面14 m时,地面高度分别为1.2 m、1.4 m、1.6 m处的电场轻度与离地面1 m高度的电场强度的差值。图示显示,在电场强度分布的拐点(电场强度的最大值和最小值)附近,差值最大,且在高压传输线路设置一定情况下,距地面越高则电场强度相对差值越大(如在铁塔中垂线下,距地1.2 m、1.4 m、1.6 m与距地1.0 m电场强度差值分别为7.53 V/m、16.4 V/m和26.7 V/m)。可以预计,在这些拐点处应该是发生高压输电线生物学效应比较明显的地方。
3.2. 高压输电线路引起的跨膜离子迁移量变化
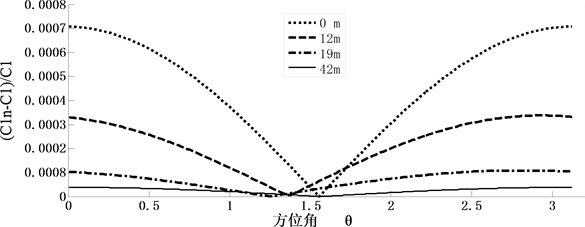
本节以细胞为电磁场的作用对象,研究高压输电线产生的生物学效应。具体讨论高压输电线产生电场对通过球心,且被xoy平面所截球形细胞平面离子跨膜迁移量的影响情况。图5给出在距离地面1.5 m处,距铁塔中垂线不同位置处,离子浓度相对变化量随方位角变化关系图(方位角 在 范围内)。
图5(a)给出距离铁塔中垂线(0点)分别为0 m、12 m、19 m和42 m处,细胞膜一侧离子浓度相对变化量相对于方位角变化关系图。图示表明:随着远离中心位置越远, 最小值位置将逐渐偏

Figure 3. Schematic diagram of electric field intensity with the distance
图3. 电场强度随距离变化关系

Figure 4. Schematic diagram of the relative change of electric field intensity varies with distance
图4. 电场强度相对差值随距离变化关系
 (a)
(a) (b)
(b)
Figure 5. Schematic diagram of (C1n – C1)/C1 with the direction angle
图5. (C1n – C1)/C1随方位角变化关系图
离90˚位置,且离中心位置越远, 最大值越小。
图3显示,在距离中心27 m处电场强度取最小值。图5(b)给出在该点附近跨膜迁移离子浓度相对变化量随 变化关系图。从图中可以看出,在电场强度取最小值时, 最大值位于0.406 π方向,而在小于27 m范围,空间位置越接近27 m处, 最小值越接近0.406 π,且跨膜迁移离子浓度相对变化量最大值越小;同样,当空间距离大于27 m时,最小值逐渐靠近0.406 π,且最大值逐渐增加。
正常细胞内的胞浆钙离子(二价)浓度为0.1 μM,细胞外的钙浓度为1000 μM,二者的固有比值为10−4量级。前述参数的高压输电线路在距离铁塔中垂线较近位置,如小于19 m范围内,可使细胞膜一侧二价离子浓度相对变化量发生10−4量级的改变,即使在产生的电场强度最小的27 m附近范围内,让可引起10−5量级的改变。牛中奇研究 [8] 表明:10−6量级的二价离子浓度的变化,就可引起细胞膜去极化,引起细胞膜电位的反转,继而引起动作电位而使可兴奋细胞兴奋。虽然本讨论研究的高压输电线路产生的电场直接作用的对象是单细胞模型,但高压输电线产生的细胞效应,如使可兴奋细胞兴奋确是无需置疑的,且其深层次的生物学效应研究有待进一步讨论。
本文讨论发现,在高压输电线下不同位置细胞引起的跨膜电位不同,引起的离子跨细胞膜迁移量不同。可以推测,细胞电穿孔可能在细胞跨膜迁移相对量大的地方发生。
4. 结论
细胞膜是电磁场作用的靶部位。高压输电线路产生电磁场,对处于其中的细胞,通过膜电位的变化对细胞膜内外离子浓度进行调制,使得细胞对外界刺激做出恰当的响应。本文以细胞一侧离子浓度变化作为研究对象,分析了220 KV哈东同塔双回三相输电线路对单细胞膜一侧离子浓度变化的影响。数值分析显示:高压输电线路距离地面高度越高,产生的电场强度越小;距离输电线铁塔中垂线距离不同,在细胞膜一侧引起的离子跨膜迁移量的变化最大值、最小值位置也不同。高压输电线路将引起细胞电磁场生物学效应。同时,本文分析方法、以及所做的数值分析,也可作为电磁场生物学效应机理研究的基础理论。
基金项目
陕西省科技发展计划(项目号:2016JM6053),咸阳师范学院重点项目(XSYK18094)。
文章引用
张小娣,马 晴,周永军,张辉. 高压输电线路对细胞膜一侧离子浓度影响分析
Modulation of Ion Concentration of Isolate Cell Exposed to the Electric Field of High-Voltage Transmission Line[J]. 生物物理学, 2018, 06(03): 43-49. https://doi.org/10.12677/BIPHY.2018.63004
参考文献
- 1. 张可心. 超高压传输线电磁环境特性研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2009.
- 2. Yi, G.S., Wang, J., Han, C.X., et al. (2012) Spiking Patterns of a Minimal Neuron to ELF Sinusoidal Electric Field. Applied Mathematical Modelling, 36, 3673-3684. https://doi.org/10.1016/j.apm.2011.11.012
- 3. Che, Y.Q., Wang, J., Si, W.J., et al. (2009) Phase-Locking and Chaos in a Silent Hodgkin-Huxley Neuron Exposed to Sinusoidal Electric Field. Chaos Soliton and Fractals, 39, 454-462. https://doi.org/10.1016/j.chaos.2007.03.008
- 4. Che, Y.Q., Wang, J., Deng, B., et al. (2012) Bifurcations in the Hodgkin-Huxley Model Exposed to DC Electric Fields. Neurocomput, 81, 41-48. https://doi.org/10.1016/j.neucom.2011.11.019
- 5. Yi, G.S., Wang, J., Wei, X.L., et al. (2014) Dynamic Analysis of Hodgkin’s Three Classes of Neurons Exposed to Extremely Low-Frequency Sinusoidal Induced Electric Field. Applied Mathematics and Computation, 231, 100-110. https://doi.org/10.1016/j.amc.2013.12.181
- 6. 伊国胜, 王江, 魏熙乐, 邓斌. 无创式脑调制的神经效应研究进展[J]. 科学通报, 2016, 61(8): 819-834.
- 7. Ma, J. and Tang, J. (2015) A Review for Dynamics of Collective Behaviors of Network of Neurons. Science China Technological Sciences, 58, 2038-2204. https://doi.org/10.1007/s11431-015-5961-6
- 8. 牛中奇, 王海彬, 侯建强, 等. 电磁波对细胞内外离子浓度影响的基本理论[J]. 中国医学工程学报, 2002, 21(6): 552-556.
- 9. 张辉, 许家栋, 牛中奇. 离子跨膜迁移的几率波理论[J]. 生物医学工程学杂志, 2007, 24(2): 257-261.
- 10. 张辉, 许家栋, 牛中奇, 等. 离子跨膜迁移几率对电磁波的响应[J]. 中国医学物理学杂志, 2004, 21(3): 179-181.
- 11. 张辉, 王李阳, 张培杰, 等. 静电场调制椭球形细胞膜电位和一侧离子浓度的研究[J]. 中国科学, 2018(7): 783-790.
- 12. 张辉, 王李阳, 张小娣, 等. 脉冲波对离子跨膜迁移的影响[J]. 西北大学学报(自然科学版), 2017, 47(4): 481-487.
- 13. 童碧云. 500 kV高压输电线路电磁环境计算及控制研究[D]: [硕士学位论文]. 浙江大学, 2011.
- 14. 李辑熙, 牛中奇. 生物电磁剂量学概论[M]. 西安: 西安电子科技大学出版社, 1990.