Journal of Aerospace Science and Technology
Vol.04 No.04(2016), Article ID:19426,11
pages
10.12677/JAST.2016.44011
Thermal-Fluid-Solid Coupling Analysis of Aero-Engine Nozzle
Pei Luo, Min Zheng
College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu

Received: Dec. 9th, 2016; accepted: Dec. 26th, 2016; published: Dec. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The aero-engine nozzle works in the high temperature and high pressure environment, which is affected by the complex loads. The thermal load and the aerodynamic load are the main factors influencing the nozzle durability. Aiming at the problem of thermal-fluid-solid coupling for nozzle affected by high intensive pressure and high constant temperature, on the basis of finite element analysis, this paper applies ANSYS to build technology roadmap simulating one-way three fields coupling of an aircraft engine nozzle. Simultaneously, by means of analyzing main coupling characteristics, the results show the relationship among temperature field, flow field and the structure in the modal analysis, which has significant meaning in the design process of nozzle.
Keywords:One-Way Thermal-Fluid-Solid Coupling, Finite Element, Nozzle

航空发动机尾喷管热流固耦合分析
罗沛,郑敏
南京航空航天大学民航学院,江苏 南京

收稿日期:2016年12月9日;录用日期:2016年12月26日;发布日期:2016年12月29日

摘 要
航空发动机尾喷管运行在高温高压的环境中,持续受到复杂载荷影响,其中热载荷和气动载荷是影响尾喷管寿命的主要因素。为了探究不同工作状态下尾喷管的结构动态特性,本文基于有限元分析方法,通过建立仿真技术路线,采用单向热流固耦合方法模拟尾喷管的工作过程,得到模态参数和振型。通过对相同振型在不同工作状态下频率变化的对比分析,揭示了温度场、流场和结构之间的作用关系,这在尾喷管的研制试验中具一定的指导意义。
关键词 :单向热流固耦合,有限元,尾喷管

1. 引言
随着全球航空工业技术的不断发展,航空发动机已经从过去的活塞式发展成为现在广泛使用的涡轮式 [1] 。涡轮发动机是一种高效精密的动力装置。通常来说,它包括压气机、燃烧室、涡轮和尾喷管,如图1 [2] 所示。
尾喷管是航空发动机排气系统的核心部件,它将流过涡轮的燃气加速膨胀,让燃气热能转换为动能以高温高压气流的形式向后喷出,进而产生推力。由于尾喷管的工作环境十分恶劣,常被高温高压的气体包围,工作环境的改变将影响尾喷管性能,进而影响发动机的整体性能。其安全性和持续改进备受关注,而温度场、流场和结构的相互作用是影响工作环境的重要因素 [3] 。发动机工作时,通过涡轮的燃气产生热载荷和气动载荷施加尾喷管的内表面,这些载荷可会引起尾喷管结构疲劳,甚至导致整个发动机的失效 [4] 。因此,在航空发动机尾喷管的研究试验中,热流固耦合特性需要被充分考虑。
在这个方面,国内外许多的学者进行了相关研究。例如,Patankar提出了用于热传递和其与流场相互作用的简便算法 [5] 。Matarazzo讨论了如何模拟热场在结构上的影响 [6] 。Ji总结归纳了航空发动机燃烧室数值仿真方法的发展情况,可以借鉴来对尾喷管的分析 [7] 。董红等对燃烧室的流固耦合进行了数值模拟,比较精确的模拟了火焰筒上温度的分布 [8] 。杨万里等研究了燃烧室热应力的分布情况 [9] 。高金海等对火焰筒进行热流固耦合仿真,探索了燃烧模型的有效性 [10] 。
国内外对航空发动机尾喷管的热流固耦合的研究却比较少,不同结构的动态特性往往不同。为了探索尾喷管在工作状态下的动态性,本文基于有限元分析方法,利用Ansys软件构建仿真技术路线,对尾喷管进行热流固耦合分析。
2. 热流固耦合方法
热流固耦合问题一个包含了热力学、流体力学和固体力学的交叉问题。从理论推导入手,其遵循质量守恒、动量守恒、能量守恒和固体控制方程 [11] [12] 。

Figure 1. Basic structure of turbojet engine
图1. 涡轮喷气发动机基本结构
质量守恒方程用来描述质量的连续性,即单位时间内流出质量等于单位时间内流入质量。质量守恒方程的微分形式可以被写成如下形式 [13] :
(2-1)
其中vx、vy和vz是速度在x、y、z方向上的分量,t是时间,ρ是密度。此处引入哈密顿算子:
(2-2)
因此,方程2-1进一步得到:
(2-3)
动量守恒方程用来描述流体单元受外界作用力与时间的关系,其微分形式可以写成如下形式 [14] :
(2-4)
其中,p是压力,ςxx、ςxy、ςxz是粘性应力的分量,αx、αy、αz是在三个方向上的加速度。
由于热流固耦合涉及热力学问题,必然要考虑到热力学定律,即能量方程用来描述整个系统的热交换状态,其微分形式可以被写成如下形式 [15] :
(2-5)
其中,E是流体总能量,k是热传导系数,S是熵。
最终目的是求解结构响应,固体控制方程用来描述流体激发结构振动位移的状态,其微分形式可以写成如下形式 [16] :
(2-6)
其中,M是质量矩阵,D是阻尼矩阵,S是刚度矩阵,ς是作用在结构上的力,x是位移。
分析温度场、流场和结构之间的相互关系,求解热流固问题的过程,其实也就是求解流体域和结构之间耦合方程的过程。从计算角度来说,其实也是找到一个N-S方程和非线性结构动态方程之间的集合算法 [17] 。一般来说,有两种求解耦合方程的思路。一种是基于单向耦合的数据单向传输算法,另一种是基于双向耦合的数据双向传输算法 [18] [19] 。
由于现在的分析软件只能支持最多两个场的双向耦合,而本文研究涉及流场、温度场和结果这三个场的耦合问题,所以采取单向耦合方法来研究热流固问题。单向热流固耦合原理如图2 [20] 。
单向热流固耦合,先对流场进行分析,得到热载荷和压力载荷。将热载荷加到结构上,进行热分析,得到热应力。最后,将压力载荷和热应力加到结构上,采集响应信号经过处理得到模态参数和振型 [20] 。
双向热流固耦合,则对流场分析得到热载荷和压力载荷。特别的是,将压力载荷加载结构上后,此时结构分析并不是马上计算响应,而是计算结构反作用到流场的压力载荷。将反向的压力载荷加到流场
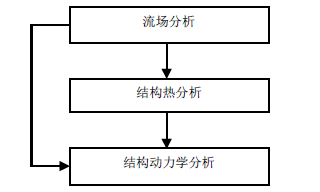
Figure 2. One-way Thermal-Fluid-Structural coupling principle chart
图2. 单向热流固耦合原理图
上,接着计算流场对结构的压力载荷,如此反复进行!热载荷亦复如是!从以上描述可以知道,双向热流固耦合比单向热流固耦合复杂,另一方面,双向耦合也更符合实际结构受载情况 [20] 。
在解决实际问题时,常通过理论推导求解耦合方程,但解析法只能求解相对简单的问题 [21] 。面对包含复杂条件的问题,往往采用数值计算方法和计算机辅助技术来处理非线性偏微分问题,因为这种问题很难推导出解析解。有限差分法和有限元法是两种在数值计算中常用的方法 [22] 。有限元法,即是将目标物分成若干个小块并为每个小块建立自由度方程,然后他们被集合进系统方程来仿真出整体模态 [23] 。本文将采用有限元法来进行建模计算。同时,通过计算机辅助工程技术来完成对热流固耦合问题的仿真。仿真流程如图3所示 [24] 。
3. 尾喷管模型和网格划分
本文采用的仿真软件是美国ANSYS公司开发的ANSYS 17.0有限元分析软件,该软件可以进行热场、流场和结构分析,符合本文的仿真需求 [24] 。
现实中,为了满足不同用途飞机的推进要求,尾喷管结构形状和尺寸大小也不尽相同。为了研究尾喷管的热流固耦合问题,将建立一个收敛型尾喷管的简化模型,即是忽略其复杂的内部结构,同时只考虑高温高压的空气流而不是预混气体,如图4所示。
然后,在结构空腔内建立流体域。对流体域和结构进行网格划分。特别注意到,在进行热流固耦合分析时,由于流体受热膨胀,流体的外层部分需要设置膨胀层。于是,创建一个包括4289个节点和8949个单元的网格划分,如图5所示。
4. 模态分析和耦合计算
模态分析即是求解固体控制方程的特征值和特征向量,需要定义材料的弹性模量、泊松比和密度 [25] 。流体域材料选择软件材料库的空气。结构材料采用不锈钢310s作为尾喷管材料,针对0℃、300℃、600℃对结构进行单向热流固特性分析,其性能参数如表1。
首先计算无预应力的模态,选择Modal模块,设置宽阔端固定,环境温度0℃,作为参考基准。得到六个模态形变和相应频率,如图6和表2所示。
为了实现热流固耦合,将运用Fluent、Steady-State Thermal和Static Structure这三个模块来进行分析。在Fluent中,设置能量方程打开,由于空气流是一种高温高压高雷诺数的流,所以选择k-epsilon粘性模式。特别需要注意的是,需要在流体与结构之间设置一个耦合面。Fluent的计算结果如图7,图8所示。
经过Fluent分析后,将流固耦合面上分布的温度场导入Steady-State Thermal模块并计算结构上的温度分布。然后,将热场计算结果导入Static Structural模块,如图9所示。

Figure 3. Analysis flow chart
图3. 分析流程图

Figure 4. Simplified nozzle model
图4. 尾喷管简化模型

Figure 5. Fluid field and structural meshing
图5. 流体域与结构的网格划分
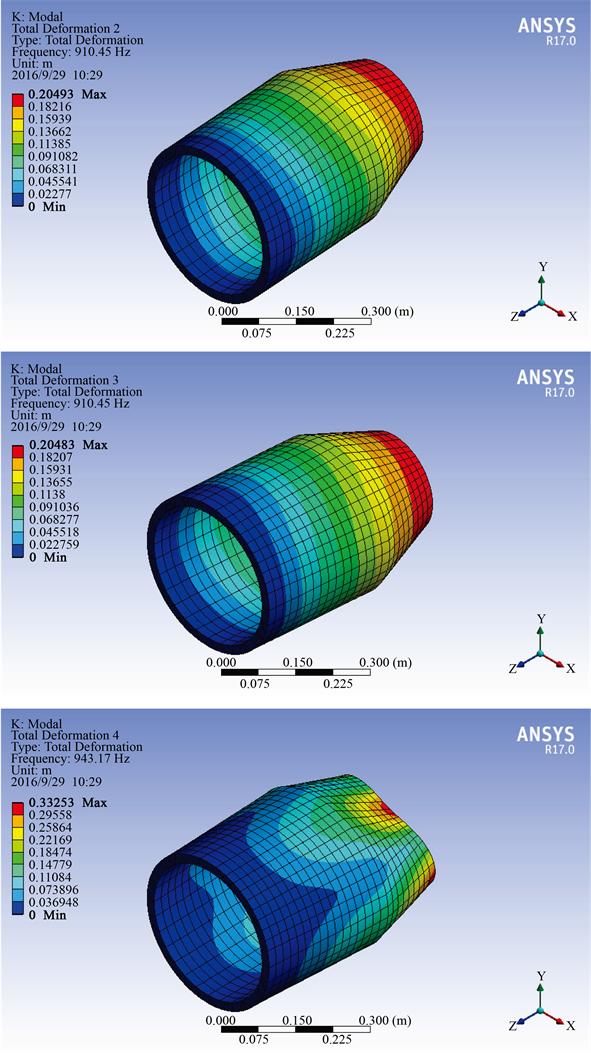

Figure 6. Nozzle Six Vibration modes by no-pre-stress modal analysis
图6. 尾喷管在无预应力模态分析中的六阶振型

Figure 7. Temperature distribution of fluid field and structural in the YZ plane
图7. 流体域和结构域在YZ平面上的温度分布

Figure 8. Velocity distribution of fluid field and structural in the YZ plane
图8. 流体域和结构域在YZ平面上的速度分布

Figure 9. Temperature load on the nozzle
图9. 施加在尾喷管上的温度载荷
Table 1. Structural material properties
表1. 结构材料特性
Table 2. Modal data
表2. 模态数据
同时,将Fluent模块中流体膨胀面上产生的压力载荷施加在Static Structural模块,如图10所示。
在加载了温度载荷和压力载荷后,在Static Structural模块中进行预应力模态分析。分析结果揭示了温度、流体速度和结构模态参数之间的相互关系,如表3~5所示。
5. 结论
旨在对尾喷管进行热流固耦合分析,借助有限元仿真软件ANSYS,运用单向热流固耦方法,通过对结构在不同工况下的模态分析,我们可以得到如下的结论:
1) 随着温度的升高,各阶振型的频率显著降低。由于温度的升高会导致材料密度降低,密度的降低进一步导致杨氏模量降低,从而使相同振型频率降低。

Figure 10. Pressure load on the nozzle
图10. 施加在尾喷管上的压力载荷
Table 3. Modal data (flow velocity = 100 m/s)
表3. 模态数据(流速 = 100 m/s)
Table 4. Modal data (flow velocity = 200 m/s)
表4. 模态数据(流速 = 200 m/s)
Table 5. Modal data (flow velocity = 300 m/s)
表5. 模态数据(流速 = 300 m/s)
2) 随着流速的升高,部分振型的频率轻微降低,部分振型频率变化不明显;阶数越高,其频率降低的幅度也越大。由于流场力对结构体的作用,造成结构形变,进而影响密度和杨氏模量,所以会有一定的影响。但总体言,流速对模态影响不明显。
综上所述,温度对结构模态产生显著影响,而流速对结构模态的影响不显著。
参考文献 (References)
[1] 陈忠军, 刘熊. 燃气涡轮发动机基础[M].北京: 中国民航出版社, 2014.
[2] (2007) Archives of Pearson Scott Foresman. https://commons.wikimedia.org/wiki/File:Combustion_chamber_(PSF).png
[3] 彭泽琰, 刘刚, 桂幸民, 等. 航空燃气轮机原理[M]. 北京: 国防工业出版社, 2008.
[4] 廉筱纯, 吴虎. 航空发动机原理[M]. 西安: 西北工业大学出版社, 2005.
[5] Patankar, S.V. (1980) Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing Corp, Carlsbad.
[6] Matarazzo, S. and Laget, H. (2011) Modelling of the Heat Transfer in a Gas Turbine Liner Combustor. Proceedings of the 7th Mediterranean Combustion Symposium, Chia Laguna, September, 56-68.
[7] Ji, Y.Z. (2003) The Status and Development of the Numerical Simulations of an Aero-Engine Combustion Chamber. Aero-Engine, 29, 25-29.
[8] 高金海, 王建军, 马艳红, 洪杰. 基于热-流-固耦合方法火焰筒壁温三维数值模拟[J]. 北京航空航天大学学报, 2011(3): 981-985.
[9] 董红, 闻雪友, 李名家, 贺星. 环管型燃烧室火焰筒壁温气热耦合数值模拟[J]. 航空动力学报, 2014(5): 1071-1078.
[10] 杨万里, 陈国华, 王春发, 叶晓明. 内燃机燃烧室零件动态热应力研究[J]. 内燃机工程, 2002(3): 46-49.
[11] 赵文胜. 轴向流中板结构流固耦合动力学研究[D]: [博士学位论文]. 武汉: 武汉大学, 2011.
[12] 白洁. 发动机歧管式催化转化器热流耦合分析[D]: [硕士学位论文]. 武汉: 武汉理工大学, 2011.
[13] Pedlosky, J. (1987) Geophysical Fluid Dynamics. Springer, New York, 10-13. https://doi.org/10.1007/978-1-4612-4650-3
[14] Batchelor, G.K. (1967) An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge.
[15] Wesseling, P. (2001) Principles of Computational Fluid Dynamics. Springer-Verlag, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-05146-3
[16] Olson, L.G. and Bathe, K. (1985) Analysis of Fluid-Structure Interactions. A Direct Symmetric Coupled Formulation Based on the Fluid Velocity Potential. Computers & Structures, 21, 21-32. https://doi.org/10.1016/0045-7949(85)90226-3
[17] 周红梅, 于胜春, 王宏伟, 赵汝岩. 固体火箭发动机点火过程流固耦合仿真研究综述[J]. 推进技术, 2008(7): 54-57.
[18] 谢超. 汽车空调离心通风机气动噪声双向流固耦合分析与优化[D]: [硕士学位论文]. 长沙: 湖南大学, 2014.
[19] 邵学博. 基于ANSYS的机翼的流固耦合分析[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2011.
[20] 孟再强. 透平膨胀机叶轮流热固耦合数值模拟及分析[D]: [硕士学位论文]. 上海: 上海交通大学, 2013.
[21] 吴云峰. 双向流固耦合两种计算方法的比较[D]: [硕士学位论文]. 天津: 天津大学, 2009.
[22] 靳交通, 刘力根, 邓航, 冯学斌, 彭超义, 曾竟成. 基于有限差分法和有限元法的大型风电叶片刚度计算[J]. 机械设计与研究, 2012, 28(6): 83-85.
[23] Reddy, J.N. (2006) An Introduction to the Finite Element Method. McGraw-Hill Press, Columbus.
[24] (2016) ANSYS Release 17.0 User Documentation.
[25] 胡海岩. 机械振动基础[M]. 北京: 北京航空航天大学出版社, 2005.
