Clean Coal and Energy
Vol.06 No.01(2018), Article ID:25817,10
pages
10.12677/CCE.2018.61001
Analysis of Factors Affecting Fuel Efficiency
Fengjiao Yi*, Haoda Wang
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong

Received: Jun. 21st, 2018; accepted: Jul. 4th, 2018; published: Jul. 11th, 2018

ABSTRACT
With the rapid development of the automotive industry, energy and environmental issues have followed, and it is of great significance to improve the fuel efficiency of automotive engines. This article is based on vehicle displacement, horsepower, vehicle length, vehicle weight and other indicators, using fuel efficiency as a dependent variable, and vehicle index as an independent variable to establish a regression model. Focusing on the problem of multicollinearity in the model, we try to use the variable selection method, stepwise regression method, principal component regression method, Ridge regression and Lasso, and partial least squares method to improve the common multiple linear regression model, and compare various methods. The advantages and disadvantages are selected from the best methods.
Keywords:Fuel Efficiency, Regression Model, Regression Diagnosis, Multicollinearity
燃油效率影响因素分析
伊凤娇*,王浩达
中国海洋大学数学科学学院,山东 青岛

收稿日期:2018年6月21日;录用日期:2018年7月4日;发布日期:2018年7月11日

摘 要
随着汽车行业的迅猛发展,能源、环境问题也随之而来,提高汽车发动机的燃油效率具有非常重要的意义。本文主要从汽车排量、马力、车长、车重等指标出发,以燃油效率为因变量,以汽车指标为自变量建立回归模型。重点针对模型中存在的多重共线性问题,尝试使用变量选择法、逐步回归法、主成分回归法、岭回归和Lasso以及偏最小二乘法对普通多元线性回归模型做了改进,并比较各种方法的优劣性,从中选取最优的方法。
关键词 :燃油效率,回归模型,回归诊断,多重共线性

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
燃油效率,定义为产生特定推力或马力使用的燃油所含的能量除以这份燃油所含的全部潜在能量,其评价指标为每加仑燃油或每千克燃油所能产生的公里数。
我国的石油消耗在过去20年里以每年5%的速度增加 [1] ,然而石油作为一种不可再成能源,其总量却在持续减少,这更加剧了石油供给与需求之间的矛盾。近年来为了缓解石油供给的压力,除了寻找新的可替代能源之外从自身出发提高石油使用效率也成为了主要的研究问题。然而关于燃油效率的影响因素有哪些的问题,不同的时期,不同的学者做了不同的探讨 [2] [3] 。但是在研究过程中常常会出现所选因素相关性太强导致模型解释性很差的问题。本文主要从汽车本身的指标出发,探讨诸如排量、马力、车长、车重等对燃油效率的影响作用,同时消除模型的多重共线性,使得其更具有实际的解释价值。
2. 符号说明及数据预处理
2.1. 符号说明
本文选取了32种汽车的燃油效率数据(见表1),并对原始数据做了单位换算,使得更符合我们的习惯(ftp://ftp.wiley.com/public/sci_tech_med/introduction_linear_regression/)。
2.2. 数据预处理
观察数据可以发现,23和25号汽车的扭力数据缺失(见表2),需要寻找合适的方法进行缺失值得填充。
通过原始数据的散点图矩阵(见图1)可以发现变量间存在较强的相关关系,特别是 与 ,其散点图几乎在一条直线上,说明三者间具有很强的相关性,因此可以采用回归的方式填补缺失值。
将数据分为两部分,一部分包含所有的完整的行,一部分由23号和25号这两行组成。使用第一部分完整的数据集,以 为因变量,以 为自变量,建立回归模型。然后将23号和25号的 带入回归方程,计算得到 作为缺失值的估计。回归模型结果如下:
该回归结果(见图2)的F检验显著,t检验也均显著,R方非常大。表明 的88.84%可以由 决定。但是模型中也存在问题,比如 高度相关,多重共线性问题非常严重,但是考虑到我们只是问了寻找一个精确的模拟出缺失值而不是为了得到一个精确的可以解释的模型,所以这个问题可以暂时忽略。
最终我们利用回归方程 补足 的取值,保证了数据集的完整性。
3. 多元线性回归模型
首先建立变量的相关系数矩阵(见表3),通过相关系数矩阵可以更直观的看出y与
Table 1. Symbol description
表1. 符号说明
Table 2. Description of missing values (NA indicates missing values)
表2. 缺失值说明(NA表示缺失值)
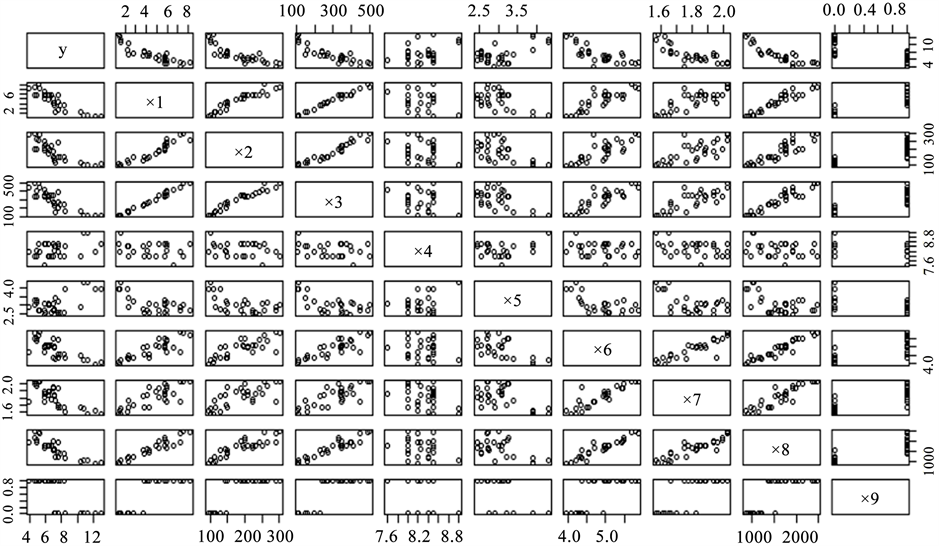
Figure 1. Scatterplot matrix
图1. 散点图矩阵

Figure 2. Regression results (x3 is dependent variable)
图2. 回归结果(x3为因变量)
Table 3. Correlation coefficient matrix
表3. 相关系数矩
具有很明显的负相关关系。y与 具有正相关关系。 为定性变量,所以并没有计算。因此可以尝试拟合全模型。
根据回归结果(见图3),全模型的F检验显著,表明模型的线性关系显著,调整后的R方达到了0.98,但是只有两个变量( )通过了t检验,而且回归系数的符号与预期不符,比如从散点图矩阵和相关系数矩阵上可以得出y与 呈负相关关系,但是回归结果 的系数为正。
以上特点都是变量间具有多重共线性的经典特征,为了进一步验证模式是否存在多重共线性问题,计算了方差膨胀因子(见表4),发现其取值非常大,证实了这个问题。
此外,多重共线性在相关系数矩阵中也有所体现,例如 和 的相关系数竟然达到了0.99,几乎是完全相关的。所以多重共线性成为了该模型中亟待解决的问题,否则该模型即使通过了显著性检验也无法进行很好的解释。
4. 多重共线性问题的解决
为了消除多重共线性,本部分分别使用了所有子集法、逐步回归法、岭回归和lasso、主成分回归法、偏最小二乘回归法,并比较了集中方法的效果,从中选出了最优的方法。
4.1. 所有子集法
根据调整后的R方,选择了R方最大的三个自变量,分别是 重新拟合多元线性回归模型,计算回归系数和方差膨胀因子(见图4)。
的回归系数符号仍然与实际相反, 的方差膨胀因子依然很大(分别为9.96和9.87),变量选择后并没有消除多重共线性(见图5)。
4.2. 逐步回归法
基于AIC和BIC的向后剔除法选择的结果都是 ,但是该变量子集已经被证明是无法消除多重共线问题的。基于AIC和BIC的向前选择法选择的结果都是x1,拟合一元线性回归并进行模型诊断后可以发现只保留一个变量(见图6)。

Figure 3. Regression results (y is dependent variable)
图3. 回归结果(y为因变量)
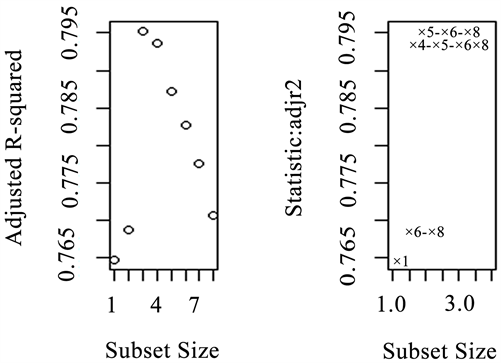
Figure 4. Plots of adj R2 against subset size for the best subset of each size
图4. 最佳子集的调整后R方
Table 4. Variance inflation factor
表4. 方差膨胀因子
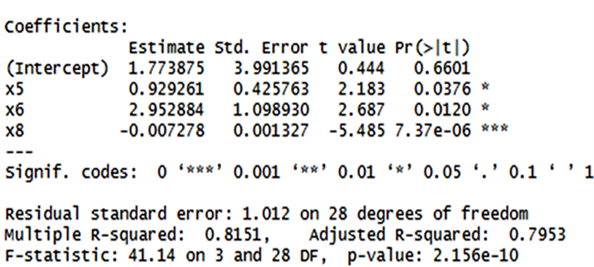
Figure 5. Regression results of all possible subsets
图5. 所有子集法回归结果
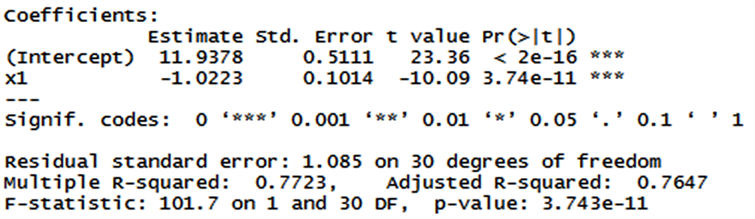
Figure 6. Regression results of stepwise methods
图6. 逐步回归法回归结果
但是这样也有弊端,只保留一个变量,损失了其他信息。标准残差图中似乎蕴含着二次项关系,信息提取不充分,只用 不能完全解释y (见图7)。
4.3. 岭回归和lasso
岭回归是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法 [4] 。
最小二乘法求解回归系数的过程中需要考虑特征矩阵是否可逆的问题,引入岭回归就是为了解决这个问题。普通最小二乘法的回归系数矩阵的估计为 ,岭回归的参数估计为
对变量做标准化(记为 等)处理后建模,最终选择了6个自变量,得到的回归结果为:
用岭回归的方法得出的回归系数与实际预期相符合了。
Lasso算法改进了最小二乘法,在估计回归系数的同时可以达到变量选择的目的 [5] 。是受约束的最小二乘法,考虑P个自变量的回归模型,在 的约束条件下,使得残差平方和最小,
使用拉格朗日乘数法
即:最小化残差的平方和加上对回归系数的绝对值的惩罚项。
当s非常大时,约束条件几乎不起作用, 结果跟普通最小二乘法相同。
当s比较小时, 较大,回归结果中有的系数等于0,我们就把等于0的系数对应的自变量删除,所以Lasso可以同时进行参数估计和变量选择。
K折交叉验证是评价模型的一种常用方法,它把所有的观测数据大致分为k等份,然后轮流以其中的所有可能的k−1份为训练集,用来拟合数据,剩下的一份为测试集,一共计算k次,得到拟合测试集时的均方误差那样的k个指标再做平均,对于每个模型都做一遍,然后选择平均均方误差最小的模型 [6] 。根据交叉验证,最佳 的简约模型是选择了 和x8 (见图8)。
Lasso做参数估计的同时也起到了了变量选择作用,选出的简约模型保留了 和 ,符号也是正确的。
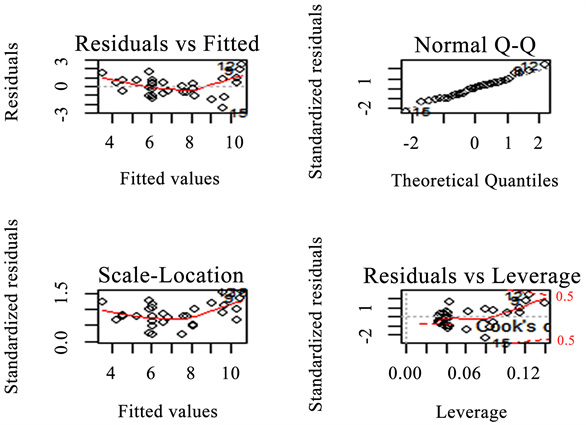
Figure 7. Model diagnostic plots
图7. 模型诊断图

Figure 8. Cross validation
图8. 交叉验证
4.4. 主成分回归法
主成分回归是将主成分变量作为自变量,建立回归模型,具体的参数估计等跟普通最小二乘法无异,主成分只是原始变量的线性组合,组合后看作一些新的变量 [7] 。因为主成分是从标准化后的数据阵出发的,所以这里也先对数据做了标准化处理。
记主成分矩阵为Z,原始变量矩阵为X,因变量为Y,则Z=XV
建立Y和Z的回归方程为 ,估计的回归方程为
再根据主成分与原始变量的关系,可以逆变换回带 ,则建立了Y和X的回归方程,其中的回归系数 。
为了消除单位和数量级的差异,对变量做了标准化处理,主成分分析(见图9)和主成分回归(见图10)结果如下:
由 可求回归结果为:
不完全主成分回归删除了V中相应的有着很小的方差对回归贡献不大的的后几列,保留前p列,回归系数也只有p个了,回归系数的估计值为 。
至于保留几列,p等于多少,有不同的标准,需要谨慎对待。这里我们看到在主成分分析中,提取两个主成分时,累计贡献率达到了81% (见图11),为了简约,我们就只保留了两个主成分。
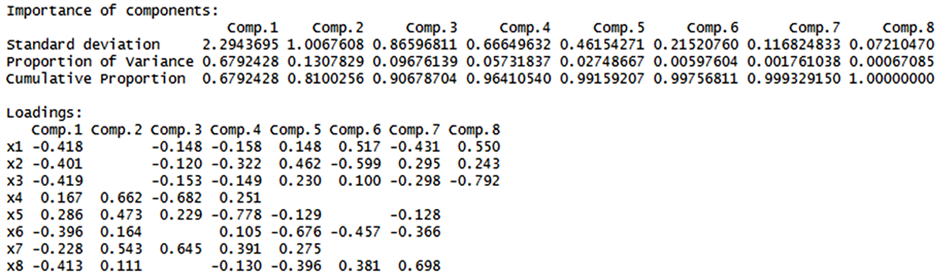
Figure 9. Principal component analysis
图9. 主成分分析
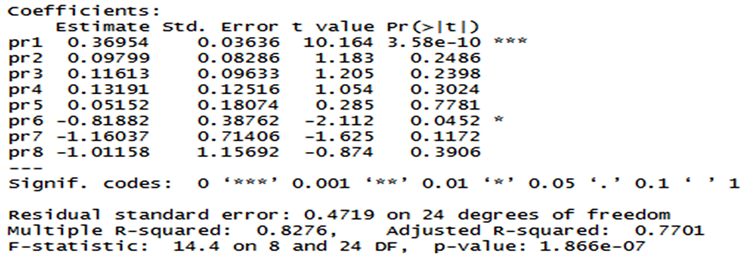
Figure 10. Principal component regression
图10. 主成分回归

Figure 11. Incomplete principal component regression
图11. 不完全主成分回归
回归结果为:
4.5. 偏最小二乘回归
偏最小二乘回归类似于主成分回归,主成分回归是在自变量中找到一些相互独立的主成分,主成分是原始变量的线性组合,用主成分代替原来的变量进行回归,以解决多重共线性问题。偏最小二乘回归则是先在因变量(如果有多个因变量)和自变量中各自寻找一个因子 [8] ,条件是这两个因子在其他可能的因子中最相关,然后在选中的这一对因子的正交空间中再选择一对最相关的因子,如此下去,直到这些因子有充分的代表性为止(可以用交叉验证)。
图12中,横坐标均表示自变量因子的个数。左图纵坐标表示RMSEP (root mean squared error of prediction),黑线表示留一法计算结果,红线表示调整后留一法计算结果,RMSEP越小越好。中图纵坐标表示MSEP (mean squared error of prediction),黑线表示留一法计算结果,红线表示调整后留一法计算结果,MSEP越小越好。右图纵坐标表示R方(R-squared),R方越大越好。
根据交叉验证的结果(见图12),无论是RMSEP、MSEP还是R方准则,都是因子个数为2时最好,但是一个因子和两个因子,三个准则几乎相差无几,为了简约,还是选择一个因子,回归结果如下:
4.6. 比较
通过实例比较,我们发现在多重共线性严重存在的情况下,三种有偏回归方法(主成分回归;岭回归和lasso,偏最小二乘回归)在建立模型和预测因变量方面优于普通回归模型,也优于变量选择和删除变量法。因为主成分是原始变量的线性组合,可以代表原始变量的信息,而且主成分之间没有相关性,所以可以避免多重共线性问题,偏最小二乘回归类似;岭回归和lasso对回归系数加入惩罚项,避免参数估计值过大,降低共线性的影响,lasso的惩罚函数是绝对值形式,还可以剔除多重共线性强的变量。所有子集法和逐步回归法选择出的模型要么仍然存在多重共线性问题,要么只选择了x1一个自变量,对y的信息解释不充分。删除变量法原则上是删除一些相关性大的、影响力小的自变量,但是缺乏客观的评价标准,需要专业的知识做支撑。
但这三种有偏方法建立的模型哪个更好,不同的问题和不同的判别标准,答案是不同的 [9] 。通常而言,在追求预测效果时,我们可以首先试用偏最小二乘回归方法,而要想对回归系数进行直观的控制时,可首选岭回归;而对某些综合因素特别关心需要把它拟合进回归方程时,可考虑选用主成分回归。不能偏心哪一种方法,回归效果要和实际情况相对照。
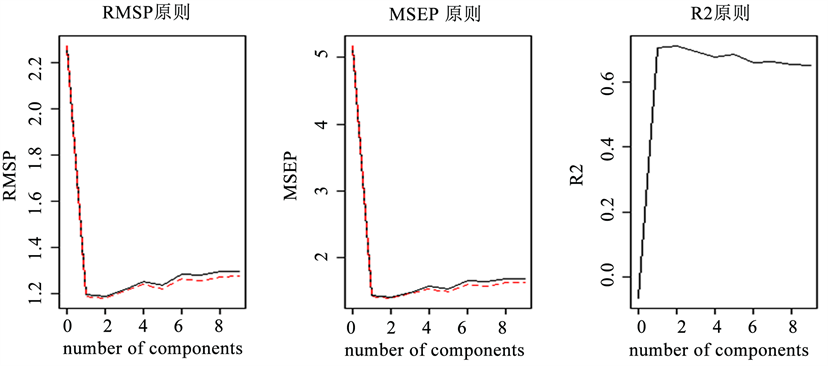
Figure 12. Partial least squares regression cross validation results
图12. 偏最小二乘回归交叉验证结果
5. 结论
本文主要从汽车本身的指标出发,探讨诸如排量、马力、车长、车重等对燃油效率的影响作用。根据建模结果,燃油效率与排量、马力、扭力、车长、车宽、车重呈正相关关系,排量和车重对燃油效率的影响作用最大。压缩比率、后轴比率对燃油效率有正的影响,但是影响作用不大。变速器的类型未体现出对燃油效率的影响。另外,汽车的上述指标之间存在很强的相关关系,比如排量、马力、扭力之间,车长、车宽、车重之间相关系数几乎达到了0.9,多重共线性是需要重点讨论的问题,通过五种方法的比较,主成分回归;岭回归和lasso,偏最小二乘回归表现较好。
本文虽然得到了一些指导性的结论,但仍有很多不足之处。比如数据集来源于国外网站,没有纳入针对国内自主品牌汽车的数据,下一步,将考虑量化国产车诸多指标对燃油效率的影响。其次限于篇幅,本文未展开论述不同回归方法的理论内涵,将来会更加深入的探索每种方法的理论,并尝试优化改进算法。最后,在后续研究中,将尝试加入影响燃油效率的其他方面的因素,探讨诸如汽车先进节油技术、汽车保养状况、胎压、润滑油、驾驶操作规范水平等对燃油效率的影响。
文章引用
伊凤娇,王浩达. 燃油效率影响因素分析
Analysis of Factors Affecting Fuel Efficiency[J]. 清洁煤与能源, 2018, 06(01): 1-10. https://doi.org/10.12677/CCE.2018.61001
参考文献
- 1. 潘虹如. 燃油税改革: 小排量、新能源汽车受宠[J]. 标准生活, 2009(1): 41-43.
- 2. 王登峰, 邓阳庆, 刘延林, 等. 汽车使用诸因素对燃油经济性的影响分析与试验研究[J]. 公路交通科技, 2008, 25(8): 150-153.
- 3. 陈海涛. 汽车结构因素对燃油经济性的影响[J]. 公路与汽运, 2006(2): 1-4.
- 4. 陈晓停, 曹兰杰, 汪金花. 岭估计在多项式曲面拟合GNSS高程中的应用[J]. 河北联合大学学报(自然科学版), 2016, 38(4): 1-6.
- 5. 张秀秀, 王慧, 田双双, 等. 高维数据回归分析中基于LASSO的自变量选择[J]. 中国卫生统计, 2013, 30(6): 922-926.
- 6. 龙泽海, 杨毅, 赵月丽. 基于lasso方法的银行对中小企业贷款供给意愿研究[J]. 金融与经济, 2017(3): 58-65.
- 7. Massy, W.F. (1965) Principal Components Regression in Exploratory Statistical Research. Publications of the American Statistical Association, 60, 234-256. https://doi.org/10.1080/01621459.1965.10480787
- 8. 林育贤, 冯圣红. 基于PCA法的BP网络对冰蓄冷系统的空调负荷预测[J]. 建筑节能, 2016(7): 13-15.
- 9. 龙泽海, 杨毅, 赵月丽. 基于lasso方法的银行对中小企业贷款供给意愿研究[J]. 金融与经济, 2017(3): 58-65.
NOTES
*通讯作者。
