Pure Mathematics
Vol.07 No.04(2017), Article ID:21346,5
pages
10.12677/PM.2017.74036
On Criterion of Arc-Transitive Cayley Graphs
Xue Yu
School of Mathematics and Statistics, Yunnan University, Kunming Yunnan

Received: Jun. 22nd, 2017; accepted: Jul. 7th, 2017; published: Jul. 13th, 2017

ABSTRACT
In 1938, R. Fruchet proved that for any given abstract group, there is a graph of it as an automorphism group. Since then, this area, which is about using the groups to study the graphs, opened the curtain. However, extensive research in this area began in 1960, especially in the last 30 years, where a number of important tasks were done. In this paper, we study a branch of graph theory that is, Cayley graph and its decision, especially the arc transitive graph. Firstly, by studying the properties of graph and the exchange of group, we get the main theorem of this paper. Secondly, according to the definition of the normal arc transitive graph and the pushing process of the main conclusion, a judgment condition of the normal arc transitive graph is given.
Keywords:Vertex-Transitive Graph, Arc-Transitive Graph, Cayley Graph, Orbital Graph
关于弧传递Cayley图的判定
于雪
云南大学数学与统计学院,云南 昆明
收稿日期:2017年6月22日;录用日期:2017年7月7日;发布日期:2017年7月13日

摘 要
1938年R. Fruchet证明了对于任意给定的抽象群,都存在一个图以它为自同构群。自此,关于利用群来研究图这一领域,揭开了帷幕。但是,这个领域的广泛研究则是从1960年才真正开始的,尤其是最近30年,在这方面完成了很多重要的工作。本文主要研究了图论的一个分支,即:Cayley图以及它的判定,尤其是弧传递Cayley图的判定。首先,通过研究图的性质以及群的交换性,从而得出本文的主要定理。其次,根据正规弧传递Cayley图的定义以及主要结论的推导过程,得出了一个关于正规弧传递Cayley图的判定条件。
关键词 :边传递图,Cayley图,弧传递图,Orbital图

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文假设所研究的群是有限群,图是有限的连通的简单的图。在图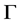 中,记图
中,记图 的顶点集、边集、弧集分别为
的顶点集、边集、弧集分别为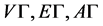 。若
。若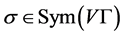 ,且
,且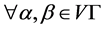 ,使得
,使得
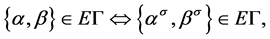
则称 为
为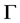 的一个自同构。
的一个自同构。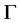 的全体自同构对于映射的复合运算构成一个群,称为图
的全体自同构对于映射的复合运算构成一个群,称为图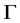 的全自同构群,记其为
的全自同构群,记其为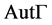 。显然有
。显然有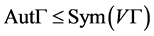 。若
。若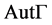 作用在
作用在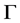 的
的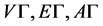 上是传递的,则分别称
上是传递的,则分别称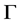 为点传递图、边传递图、弧传递图。特别地,若存在
为点传递图、边传递图、弧传递图。特别地,若存在 ,且
,且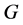 在
在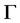 的
的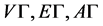 上的作用是传递的,则分别称
上的作用是传递的,则分别称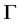 为G-点传递图、G-边传递图、G-弧传递图。此外,由文献 [1] 知:自同构群
为G-点传递图、G-边传递图、G-弧传递图。此外,由文献 [1] 知:自同构群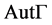 在
在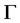 的弧集上是传递的,也就是说,
的弧集上是传递的,也就是说,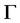 是弧传递图,等价于,
是弧传递图,等价于, 在
在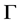 的点集上是传递的,且任一点
的点集上是传递的,且任一点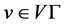 在
在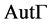 中的点稳定子群
中的点稳定子群 在
在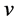 的领域
的领域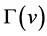 上也是传递的。由此结论,作者对弧传递图的判定,尤其是关于Cayley图的弧传递性产生了兴趣。
上也是传递的。由此结论,作者对弧传递图的判定,尤其是关于Cayley图的弧传递性产生了兴趣。
设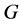 是一个群,
是一个群,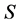 是
是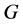 的一个不含单位元非空集合,定义图
的一个不含单位元非空集合,定义图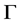 :点集
:点集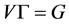 ,且任意的
,且任意的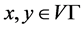 ,
,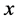 与
与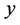 是邻接的当且仅当
是邻接的当且仅当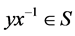 ,称
,称 是
是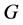 的关于
的关于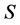 的Cayley图,记作
的Cayley图,记作 。下面给出本文的主要定理。
。下面给出本文的主要定理。
定理1.1. 设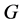 是一个群,
是一个群,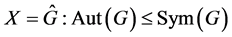 ,则下面的情况是成立的:
,则下面的情况是成立的:
1) 若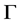 是
是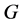 的X-边传递Cayley图,则
的X-边传递Cayley图,则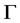 是弧传递图。
是弧传递图。
2) 若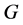 是交换群,则
是交换群,则 是X-弧传递图;若
是X-弧传递图;若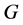 是非交换群,则
是非交换群,则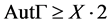 。
。
进一步地,若图 的自同构群
的自同构群 有正规子群与
有正规子群与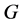 同构,且在
同构,且在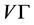 上是正则的,则称
上是正则的,则称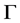 为
为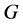 的正规Cayley图。从而可得下面的推论。
的正规Cayley图。从而可得下面的推论。
推论1.2. 设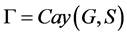 是
是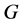 上的X-正规边传递Cayley图,若
上的X-正规边传递Cayley图,若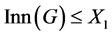 ,则
,则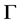 是弧传递图。
是弧传递图。
2. 预备知识
为了证明本文的主要定理,这一节将介绍一些预备的命题和引理。首先,引入Orbital图的相关命题。
设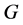 为
为 上的传递置换群,则
上的传递置换群,则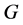 可诱导
可诱导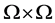 上的作用,这个作用的每个轨道,即:
上的作用,这个作用的每个轨道,即: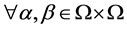 ,
,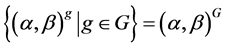 ,称为
,称为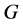 的一个Orbital。每个Orbital
的一个Orbital。每个Orbital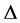 都存在一个对偶Orbital
都存在一个对偶Orbital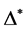 ,即:
,即: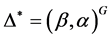 。若
。若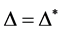 ,则称
,则称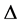 为自对偶的Orbital。称
为自对偶的Orbital。称 为广义的Orbital。设
为广义的Orbital。设 为
为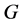 在
在 上的一个Orbital,定义图
上的一个Orbital,定义图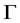 :
: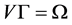 ,
,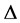 为弧集,称有向图
为弧集,称有向图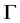 为
为 对应的Orbital图,记作
对应的Orbital图,记作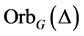 。进一步有,若
。进一步有,若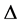 为自对偶的,则
为自对偶的,则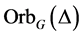 为无向图。反之亦然。易知,
为无向图。反之亦然。易知,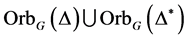 为无向图,称为广义Orbital图,通常简记为
为无向图,称为广义Orbital图,通常简记为 。
。
命题2.1. 记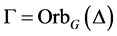 ,
,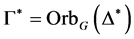 。则:
。则:
1)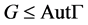 ,
,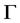 为
为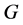 的弧传递有向图。
的弧传递有向图。
2)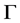 为
为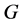 的弧传递图当且仅当
的弧传递图当且仅当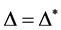 。
。
3)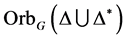 为
为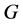 的边传递图。
的边传递图。
4)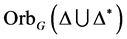 不是
不是 的弧传递图当且仅当
的弧传递图当且仅当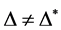 。
。
证明:
1) 因为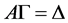 ,所以
,所以 ,则有
,则有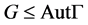 。又
。又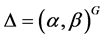 ,故
,故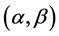 可以用
可以用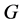 中元素射到
中元素射到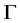 的任意一条弧,故
的任意一条弧,故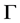 为
为 的弧传递有向图。
的弧传递有向图。
2) 由1)知: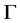 为
为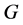 的弧传递有向图。又
的弧传递有向图。又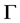 为无向图当且仅当
为无向图当且仅当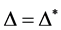 ,所以
,所以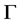 为
为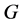 的弧传递图当且仅当
的弧传递图当且仅当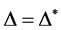 。
。
3) 设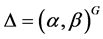 ,则有
,则有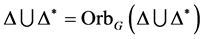 ,所以
,所以 的边集是
的边集是 ,故
,故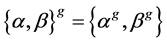 ,从而
,从而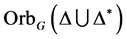 为
为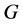 的边传递图。
的边传递图。
4) 因为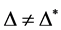 ,所以
,所以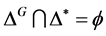 ,因此
,因此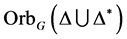 不是
不是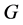 的弧传递图。反之亦然。
的弧传递图。反之亦然。
命题2.2. 设 为图,
为图,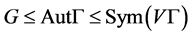 在
在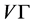 上是传递的,则下面的情况是成立的:
上是传递的,则下面的情况是成立的:
1) 若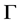 为G-弧传递图,则
为G-弧传递图,则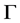 为自对偶Orbital图。
为自对偶Orbital图。
2) 若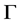 为G-边传递图,则
为G-边传递图,则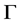 为广义的Orbital图。
为广义的Orbital图。
证明:1) 设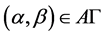 ,则
,则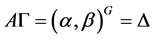 为
为 在
在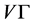 上的一个Orbital,从而
上的一个Orbital,从而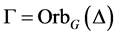 。又因
。又因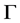 为G-弧传递图,则
为G-弧传递图,则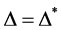 ,即:
,即: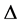 和
和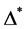 均为自对偶的。因此
均为自对偶的。因此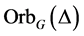 与
与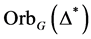 均为无向图,故
均为无向图,故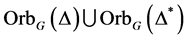 为无向图,即:
为无向图,即: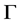 为
为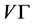 上的传递置换群
上的传递置换群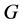 的一个自对偶Orbital图。
的一个自对偶Orbital图。
2) 因为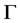 为G-边传递图,且
为G-边传递图,且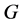 在
在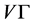 上是传递的,则
上是传递的,则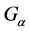 在
在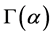 上恰有两个轨道,则
上恰有两个轨道,则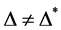 ,那么
,那么 为无向图,所以
为无向图,所以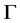 为
为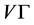 上的传递置换群
上的传递置换群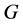 的一个广义的Orbital图。
的一个广义的Orbital图。
其次,介绍几个关于Cayley图的引理。
引理2.3. 设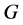 是一个群,且
是一个群,且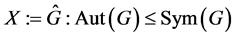 。若
。若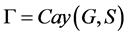 是X-边传递图,则
是X-边传递图,则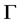 是X-弧传递图或
是X-弧传递图或 在
在 上有两个Orbital
上有两个Orbital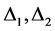 ,并且
,并且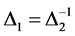 。
。
证明:由文献 [2] 可知,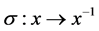 ,
,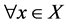 是
是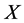 的任意Orbital到其自对偶Orbital的同构映射。故结论得证。
的任意Orbital到其自对偶Orbital的同构映射。故结论得证。
引理2.4. 设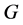 是一个群,且
是一个群,且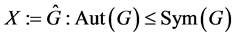 ,
,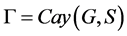 是X-边传递图,若
是X-边传递图,若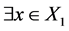 ,对一些
,对一些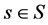 ,满足
,满足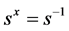 ,则
,则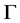 是X-弧传递图。
是X-弧传递图。
证明:在 中,
中,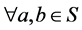 ,
,
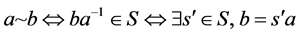
因此,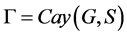 中的每一条弧均可表示为
中的每一条弧均可表示为 ,其中
,其中 。又
。又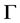 是X-边传递图,则
是X-边传递图,则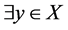 ,有
,有 。从而
。从而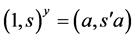 或
或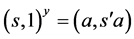 。进一步地,
。进一步地, 或
或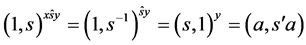 ,且
,且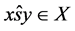 ,故
,故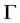 是X-弧传递图。
是X-弧传递图。
引理2.5. 设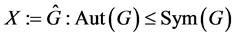 ,且
,且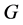 在
在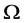 上是正则的。若
上是正则的。若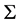 是
是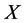 的一个Orbital,则
的一个Orbital,则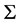 为X-弧传递图,且
为X-弧传递图,且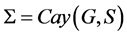 ,其中
,其中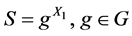 。
。
证明:因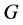 在
在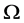 上是正则的,则可看作
上是正则的,则可看作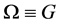 。又因
。又因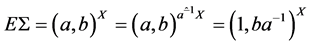 ,所以
,所以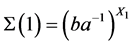 。又
。又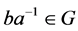 ,从而
,从而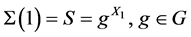 。
。
3. 定理的证明
有了前面的预备知识,本节就给出本文主要定理的证明。
定理1.1. 证明1) 因为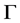 是X-边传递图,由命题2.2知,
是X-边传递图,由命题2.2知,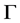 是广义的Orbital图。不妨设
是广义的Orbital图。不妨设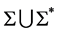 为广义的Orbital,其中
为广义的Orbital,其中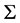 与
与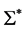 是
是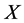 的对偶Orbital。如果
的对偶Orbital。如果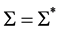 ,由命题2.1知,
,由命题2.1知,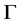 是X-弧传递图。现在假设
是X-弧传递图。现在假设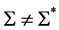 。若
。若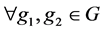 ,
,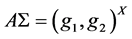 。因为
。因为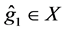 ,则
,则 。设
。设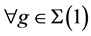 ,则
,则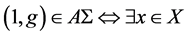 ,满足
,满足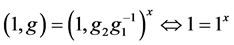 ,并且
,并且 ,那么
,那么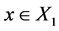 ,
,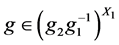 。所以
。所以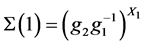 。又因
。又因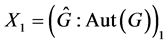 且
且 是正则的,所以
是正则的,所以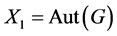 。从而
。从而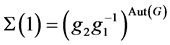 。因此我们可令
。因此我们可令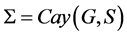 ,其中
,其中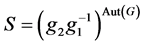 ,由引理2.3知,
,由引理2.3知,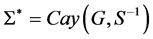 。定义一个映射:
。定义一个映射: ,
,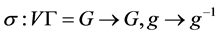 。则
。则
在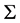 中,
中,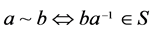
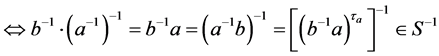
 在
在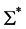 中,
中, ,
,
其中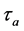 是
是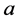 诱导的内自同构,则
诱导的内自同构,则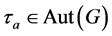 。所以
。所以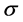 是
是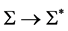 的同构映射。进一步地,
的同构映射。进一步地,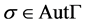 。令
。令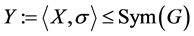 。因
。因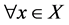 ,
,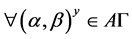 ,则
,则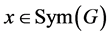 且
且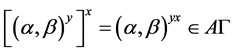 (因为
(因为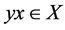 )。所以
)。所以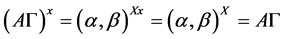 。进一步地,
。进一步地,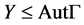 且
且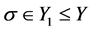 。
。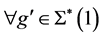 。又因为
。又因为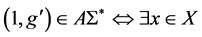 ,
,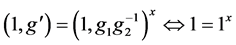 且
且 ,所以
,所以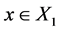 ,
,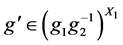 。因此
。因此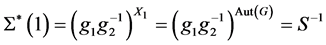 且
且 。那么
。那么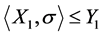 在
在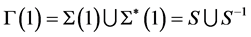 上是传递的。
上是传递的。
2) 若 是交换群,则
是交换群,则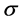 是
是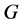 的一个同构映射,即:
的一个同构映射,即: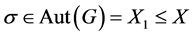 。所以
。所以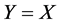 ,那么
,那么 是X-弧传递图。现在设
是X-弧传递图。现在设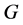 是非交换群,则
是非交换群,则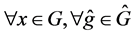 有
有
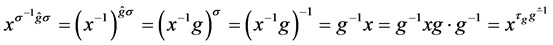 ,
,
其中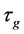 是由
是由 诱导的内自同构,且
诱导的内自同构,且 。所以
。所以 。又
。又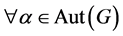 ,有
,有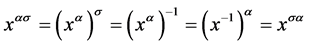 。因此
。因此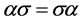 ,从而
,从而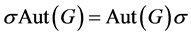 。综上,
。综上,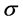 正规化
正规化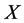 ,即:
,即: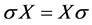 。进一步有
。进一步有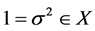 。若
。若 ,那么
,那么 。因此
。因此 ,然而
,然而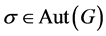 当且仅当
当且仅当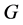 是交换群。这就产生了矛盾,所以
是交换群。这就产生了矛盾,所以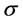 不属于
不属于 。因此
。因此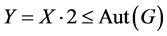 。证毕。
。证毕。
下面来证明由定理1.1得出的推论。
推论1.2的证明由文献 [3] 知,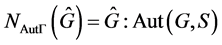 ,其中
,其中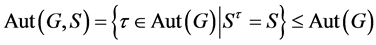 。因为
。因为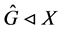 ,所以
,所以
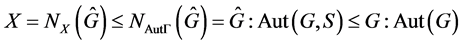 。由 [3] Frattini论断知,
。由 [3] Frattini论断知,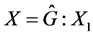 ,
, 。设
。设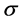 如定理1.1证明中所定义的,则有
如定理1.1证明中所定义的,则有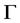 是
是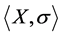 -弧传递图。证毕。
-弧传递图。证毕。
注意:1) 在推论1.2中,条件“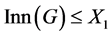 ”不可缺,否则
”不可缺,否则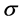 不一定是
不一定是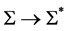 的同构映射。
的同构映射。
2) 在推论1.2中,“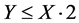 ”不一定成立。
”不一定成立。
事实上,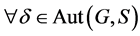 ,
,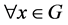 。若
。若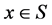 ,则
,则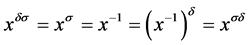 。所以
。所以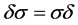 ,那么
,那么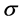 正规化
正规化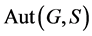 。若
。若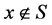 ,则
,则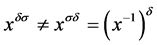 。所以
。所以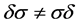 ,那么
,那么 不正规化
不正规化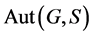 。综上,
。综上,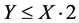 不一定成立。
不一定成立。
基金项目
国家自然科学基金《有限群的因子分解与含有传递子群的置换群(k1020531)》;云南省自然科学基金《一些对称图与Cayley图的研究(2013FB001)》;云南大学研究生科研创新基金项目资助(ynuy201688)。
文章引用
于 雪. 关于弧传递Cayley图的判定
On Criterion of Arc-Transitive Cayley Graphs[J]. 理论数学, 2017, 07(04): 277-281. http://dx.doi.org/10.12677/PM.2017.74036
参考文献 (References)
- 1. 徐明曜. 有限群导引(下册)[M]. 北京: 科学出版社, 1999.3.
- 2. Li, C.H. (2006) Finite Edge-Transitive Cayley Graphs and Rotar Cayley Maps. Transactions of the American Mathematical Society, 358, 4605-4635. https://doi.org/10.1090/S0002-9947-06-03900-6
- 3. Godsil, C.D. (1981) On the Full Automorphism Group of a Group. Combinatorial, 1, 243-256. https://doi.org/10.1007/BF02579330