Pure Mathematics
Vol.
09
No.
01
(
2019
), Article ID:
28516
,
12
pages
10.12677/PM.2019.91010
On the Decay of Higher-Order Norms of the Solutions to the Compressible Micropolar Fluids System
Liang Mao, Qingqing Liu*
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Dec. 24th, 2018; accepted: Jan. 11th, 2019; published: Jan. 18th, 2019

ABSTRACT
This paper primarily studies the decay of higher-order derivatives of the solution to the Cauchy problem on the compressible micropolar fluid system in
. The L2 norm decay rates have been investigated by Liu and Zhang [1] . We show that the decay rate of the first order spatial derivatives of solution is
by applying the Fourier splitting method and have generalized the result of the paper [1] .
Keywords:Compressible Micropolar Fluids, Fourier Splitting Method, Optimal Time Decay

可压缩微极流体系统解的衰减估计
毛亮,刘青青*
华南理工大学,数学学院,广东 广州

收稿日期:2018年12月24日;录用日期:2019年1月11日;发布日期:2019年1月18日

摘 要
本文主要研究了可压缩微极流体系统在
中柯西问题解的高阶导数的衰减估计。解的L2范数的衰减率已经被刘和张 [1] 研究,本文利用傅里叶变换的方法证明了该系统解的一阶导数的衰减率为
,推广了文 [1] 的结果。
关键词 :可压缩微极流体,傅里叶变换,衰减估计

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
我们下面考虑的系统满足下列方程:
(1.1)
该方程中的
和
分别表示密度,速度,微自转速度和压力,其中
。常数
是流体的一些粘性系数,并且满足
、
、
、
和
。
初始值为
(1.2)
在无穷远处
(1.3)
这个系统被称为微极流体模型,可以描述等熵可压缩微极流体的运动 [2] 。与经典的Navier-Stokes方程相比,这个模型引入了一种新的向量场,即粒子旋转的角速度场。在数学上,这种微旋转速度可能导致一些新的困难;物理上,微极流体可能代表由悬浮在粘性介质中的刚性、随机定向(或球形)粒子组成的流体,在这种介质中,粒子的形变被忽略,多元悬浮液、动物血液和液晶都是这种介质。
由于微极流体系统在数学和物理学的重要性,有非常多的文献研究了它的数学理论。对不可压缩的流体,也即是
为常数,
,我们可以参考文献 [3] [4] [5] 。
对于可压缩的微极流体方程,Mujaković在一维空间或具有球对称的三维空间中,对该模型解的局部存在性、整体存在性和正则性做了一系列的研究 [6] - [12] 。其他作者,如陈 [13] 证明了初始带真空的一维模型强解的整体存在性。在三维模型中,陈、黄、张 [14] 证明了柯西问题强解的爆破准则。陈、徐、张 [15] 解决了具有真空和不连续初始值的整体弱解。Mujaković和她的合作者Dražić建立了可压缩的球对称、等方性、粘性和热传导的微极流体模型,对于这个模型他们分别先后证明了齐次边界条件下解的局部存在性,整体存在性,长时间行为和解的唯一性 [16] [17] [18] [19] 。
最近,刘和张 [1] 证明了该系统的平衡解的整体稳定性和最优衰减估计,主要结果如下。
引理1.1:当
时,存在
使得
(1.4)
对于该微极流体系统的柯西问题(1.1)~(1.3)有唯一的整体解
满足
(1.5)
并且,存在
使得
(1.6)
则
满足
(1.7)
注1.1:在本文中,我们假设
,那么在引理1.1中,结合(1.4)和(1.5)可以得到
(1.8)
这里我们用
代表小量
。
受稳定性和
范数衰减结果的影响,本文的主要工作是研究该微极流体系统解的一阶衰减估计。我们的主要结果是下面的定理。
定理1.1:假设初始值
,并且满足(1.1)~(1.3)中所有的条件,那么该微极流体系统柯西问题的整体解
存在时间衰减估计为
(1.9)
最后,我们需要引入时间球
的概念,
在我们的证明中起到了非常重要的作用,它可以帮助我们通过使用低阶导数的衰减得到高阶导数的衰减估计,可以参看Navier-Stokes系统 [20] [21] 。本文用这种方法得到高阶导数的衰减估计。
注1.2:在本文中,我们用
来表示通常意义下的Sobolev空间的范数
和
来表示通常意义下的
空间的范数
。我们定义
为方便后面的使用,下面是一些需要用到的不等式。
引理1.2:若
,那么我们有下列不等式:
(1.10)
引理1.3:(Moser-type型积分不等式)若
是整数,那么就有
1) 对于
并且
,
(1.11)
2) 对于
并且
,
(1.12)
2. 微极流体系统的线性化
问题重塑
假设稳态的微级流体系统是平凡的,取
。令
。
那么
满足
(2.1)
(2.2)
(2.3)
这里的
分别为
(2.4)
其中
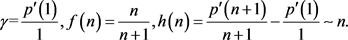
初始值为
3. 证明定理1.1
引理3.1:在(1.1)~(1.3)式的条件下,我们有
(3.1)
证明:对(2.1),(2.2),(2.3)式中左右两边同时关于空间求
阶空间导数,再分别乘以 ,然后在
上积分,我们可以得到
,然后在
上积分,我们可以得到
(3.2)
然后将
求和,我们可以得到
(3.3)
根据柯西不等式,我们知道
(3.4)
结合(3.3)和(3.4),我们可以得到
(3.5)
第一步:我们处理
这一项。
1) 当
时,根据分部积分法和引理(1.1),我们可以得到
(3.6)
类似的,我们可以得到
(3.7)
结合(3.6)和(3.7),可以得到
(3.8)
2) 当
时,利用Hőlder不等式和引理(1.1)~引理(1.3),我们可以得到
(3.9)
对于第二部分
(3.10)
利用柯西不等式和引理(1.1)~引理(1.3),我们有
(3.11)
利用分部积分法和Hőlder不等式,可以得到
(3.12)
所以,结合(3.11)和(3.12),可以得到
(3.13)
结合(3.9)和(3.13),我们有
(3.14)
对
从
到
求和,根据(3.8)和(3.14),可以得到
(3.15)
第二步:接下来处理
这一项。
1) 当
时,我们有
(3.16)
利用分部积分法,Hőlder不等式和引理(1.1)~引理(1.3),我们可以得到
(3.17)
将(3.17)代入(3.16)中,我们可以得到
(3.18)
2) 当
时。首先利用柯西不等式和引理(1.1)~引理(1.3),可以得到
(3.19)
同理,我们可以得到
(3.20)
另一方面,我们需要处理
这一项。利用分部积分法,可以得到
(3.21)
再利用柯西不等式、Hőlder不等式和引理(1.1)~引理(1.3),我们可以分别得到
(3.22)
将(3.22)代入到(3.21)中,得到
(3.23)
同理可以得到
(3.24)
将
从
到 求和,根据(3.18),(3.19),(3.20),(3.23),(3.24)得到
求和,根据(3.18),(3.19),(3.20),(3.23),(3.24)得到
(3.25)
第三步:最后我们来处理
这一项.
1) 当
时,我们有
(3.26)
类似于(3.17),我们有
(3.27)
将(3.27)代入到(3.26)中得到
(3.28)
2) 当
时。利用柯西不等式、Hőlder不等式和引理(1.1)~引理(1.3),可以得到
(3.29)
同理可以得到,
(3.30)
对于
这一项,我们先用引理(1.1)和分部积分法来处理
(3.31)
同样的我们可以得到
(3.32)
将
从
到
求和,根据(3.28)~(3.32),得到
(3.33)
第四步:将(3.5)式左右两边从
到
求和,根据(3.15)、(3.25)和(3.33),有
引理3.2:在(1.1)~(1.3)式的条件下,我们可以得到
(3.34)
证明:在方程(2.2)式中,左右两边同时取
阶导数,然后同时乘以
,得到
(3.35)
为了处理掉
这一项,我们需要用到分部积分法和方程(2.1)
(3.36)
将(3.36)代入(3.35)中得到
(3.37)
第一步:我们需要处理
这一项。当
时,利用分部积分法和柯西不等式,得到
(3.38)
当
时,利用分部积分法和引理(1.1)~引理(1.3)得
(3.39)
对
从
到
求和,根据(3.38)和(3.39)得到
(3.40)
应用柯西不等式和Hőlder不等式,得到
(3.41)
第二步:处理
这一项。当
时,类似于(3.38)可以得到
(3.45)
当
时,我们有
(3.46)
将
从
到 求和,根据(3.45)和(3.46),得到
求和,根据(3.45)和(3.46),得到
(3.47)
第三步:将(3.37)式左右两边从
到
求和,根据(3.40)、(3.41)和(3.47),有
证明定理1.1:(3.34)式乘以
加上(3.1)式,得到
(3.48)
其中
根据柯西不等式和小量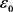 ,可以得到如下等价关系
,可以得到如下等价关系
(3.49)
根据(3.48)式,可以得到
(3.50)
对常数
我们可以定义一个时间球
然后我们就有
(3.51)
也即是
(3.52)
同理就有
(3.53)
那于是就有
(3.54)
根据(3.50)和(3.54),利用引理1.1中的衰减,得到
(3.55)
对于时间
足够大时,有
,即 ,那么就有
,那么就有
(3.56)
将(3.56)代入(3.55)中,得到
(3.57)
根据等价关系(3.49)可以得到
(3.58)
在(3.58)式中,取 ,得到
,得到
(3.59)
在(3.59)式中,左右两边同时乘以
,再同时在
上取积分,可以得到
(3.60)
所以,就可以得到
(3.61)
根据等价关系,也即是有
对所有的 。因此,我们完成了定理1.1的证明。
。因此,我们完成了定理1.1的证明。
致谢
感谢导师朱长江教授对我论文的研究方向做出的指导性意见和推荐;刘青青的研究得到国家自然科学基金(No. 11501217)和广东省自然科学基金(No. 2016A030310416)的支持。
文章引用
毛 亮,刘青青. 可压缩微极流体系统解的衰减估计
On the Decay of Higher-Order Norms of the Solutions to the Compressible Micropolar Fluids System[J]. 理论数学, 2019, 09(01): 71-82. https://doi.org/10.12677/PM.2019.91010
参考文献
- 1. Liu, Q.Q. and Zhang, P.X. (2016) Optimal Time Decay of the Compressible Micropolar Fluids. Differential Equations, 260, 7634-7661.
https://doi.org/10.1016/j.jde.2016.01.037
- 2. Eringen, A.C. (1966) Theory of Micropolar Fluids. International Journal of Mathematics and Mechanics, 16, 1-18.
https://doi.org/10.1512/iumj.1967.16.16001
- 3. Chen, Q. and Miao, C. (2012) Global Well-Posedness for the Micropolar Fluid System in Critical Besov Spaces. Differential Equations, 252, 2698-2724.
https://doi.org/10.1016/j.jde.2011.09.035
- 4. Chen, M.T. (2013) Global Well-Posedness of the 2D Incompressible Micropolar Fluid Flows with Partial Viscosity and Angular Viscosity. Acta Mathematica Scientia. Series B. English Edition, 33, 929-935.
- 5. Galdi, G.P. and Rionero, S. (1977) A Note on the Existence and Uniqueness of Solutions of the Micropolar Fluid Equations. International Journal of Engineering Science, 15, 105-108.
https://doi.org/10.1016/0020-7225(77)90025-8
- 6. Mujaković, N. (1998) One-Dimensional Flow of a Compressible Viscous Micropolar Fluid: A Local Existence Theorem. Glasnik Matematicki. Serija III, 33, 71-91.
- 7. Mujaković, N. (2001) One-Dimensional Flow of a Compressible Viscous Micropolar Fluid: Regularity of the Solution. Boundary Value Prolems, 10, 181-193.
- 8. Mujaković, N. (2005) Global in Time Estimates for One-Dimensional Compressible Viscous Micropolar Fluid Model. Glasnik Matematicki. Serija III, 40, 103-120.
- 9. Mujaković, N. (2005) One-Dimensional Flow of a Compressible Viscous Mi-cropolar Fluid: The Cauchy Problem. Mathematical Communications, 10, 1-14.
- 10. Mujaković, N. (2007) Non-Homogeneous Boundary Value Problem for One-Dimensional Compressible Viscous Micropolar Fluid Model: A Local Existence Theorem. Annali dell’Universita di Ferrara. Sezione VII. Scienze Matematiche, 53, 361-379.
https://doi.org/10.1007/s11565-007-0023-z
- 11. Mujaković, N. (2008) Nonhomogeneous Boundary Value Problem for One-Dimensional Compressible Viscous Micropolar Fluid Model: Regularity of the Solution. Boundary Value Problems, 2008, Article ID: 189748.
https://doi.org/10.1155/2008/189748
- 12. Mujaković, N. (2009) Non-Homogeneous Boundary Value Problem for One-Dimensional Compressible Viscous Micropolar Fluid Model: A Global Existence Theorem. Mathematical Inequalities & Ap-plications, 12, 651-662.
https://doi.org/10.7153/mia-12-49
- 13. Chen, M.T. (2011) Global Strong Solutions for the Viscous, Micropolar, Compressible Flow. Partial Differential Equation, 24, 158-164.
- 14. Chen, M.T., Huang, B. and Zhang, J.W. (2013) Blowup Criterion for the Three-Dimensional Equations of Compressible Viscous Micropolar Fluids with Vacuum. Nonlinear Analysis, 79, 1-11.
https://doi.org/10.1016/j.na.2012.10.013
- 15. Chen, M.T., Xu, X.Y. and Zhang, J.W. (2015) Global Weak Solutions of 3D Compressible Micropolar Fluids with Discontinuous Initial Data and Vacuum. Communications in Mathematical Sciences, 13, 225-247.
https://doi.org/10.4310/CMS.2015.v13.n1.a11
- 16. Dražić, I. and Mujaković, N. (2012) 3-D Flow of a Compressible Viscous Micropolar Fluid with Spherical Symmetry: A Local Existence Theorem. Boundary Value Problems, 2012, 69.
https://doi.org/10.1186/1687-2770-2012-69
- 17. Dražić, I. and Mujaković, N. (2015) 3-D Flow of a Compressible Viscous Micropolar Fluid with Spherical Symmetry: A Global Existence Theorem. Boundary Value Problems, 2015, 98.
https://doi.org/10.1186/s13661-015-0357-x
- 18. Dražić, I. and Mujaković, N. (2015) 3-D Flow of a Compressible Viscous Micropolar Fluid with Spherical Symmetry: Large Time Behavior of the Solution. Journal of Mathematical Analysis and Applications, 431, 545-568.
https://doi.org/10.1016/j.jmaa.2015.06.002
- 19. Mujaković, N. (2014) 3-D Flow of a Compressible Viscous Micropolar Fluid with Spherical Symmetry: Uniqueness of a Generalized Solution. Boundary Value Problems, 2014, 226.
https://doi.org/10.1186/s13661-014-0226-z
- 20. Schonbek, M.E. and Wiegner, M. (1996) On the Decay of Higher-Order Norms of the Solutions of Navier-Stokes Equations. Proceedings of the Royal Society of Edinburgh Section A, 126, 677-685.
https://doi.org/10.1017/S0308210500022976
- 21. Schonbek, M.E. (1985) L2 Decay for Weak Solutions of the Navier-Stokes Equations. Archive for Rational Mechanics and Analysis, 88, 209-222.
https://doi.org/10.1007/BF00752111
NOTES
*通讯作者。








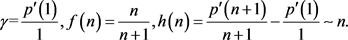
 ,然后在
上积分,我们可以得到
,然后在
上积分,我们可以得到 求和,根据(3.18),(3.19),(3.20),(3.23),(3.24)得到
求和,根据(3.18),(3.19),(3.20),(3.23),(3.24)得到 求和,根据(3.45)和(3.46),得到
求和,根据(3.45)和(3.46),得到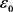 ,可以得到如下等价关系
,可以得到如下等价关系 ,那么就有
,那么就有 ,得到
,得到 。因此,我们完成了定理1.1的证明。
。因此,我们完成了定理1.1的证明。