ABSTRACT

This paper mainly uses equivalent martingale method to give the pricing formula of the geometric mean Asian reset option under fractional Brownian motion, and the relationship between the initial stock price, volatility and Hurst parameters and option price is analyzed by MATLAB.

Keywords:Fractional Brownian Motion, Asian Period, Reset Option

分数布朗运动下的亚式重置期权定价

程斯吉

广西师范大学数学与统计学院，广西 桂林

收稿日期：2019年6月5日；录用日期：2019年6月15日；发布日期：2019年6月27日

摘 要

本文主要利用等价鞅方法，给出在分数布朗运动环境下，几何平均亚式重置期权的定价公式，并利用MATLAB软件分析了初始股票价格、波动率和Hurst参数与期权价格的关系。

关键词 :分数布朗运动，亚式期权，重置期权

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

期权是金融市场上最基本的金融衍生工具之一，它是金融衍生工具创新设计的基础 [1] 。期权是金融衍生品中的一个重要组成成员，是风险管理工具中常用的一类，它是收益无限而风险有限的一类衍生工具。股票期权是一种金融期权，是重点的研究对象 [2] 。

1900年法国数学家L. Bachelier第一次引用了Brown运动的严格数学描述，得到了在到期日时股票期权价格的期望值公式，宣告了金融数学的诞生。1973年Black和Scholes [3] 发表了著名的Black-Scholes公式，建立了看涨期权定价公式，推动了期权交易的快速发展，使得期权成为世界金融市场的主要工具，因此，获得了1997年诺贝尔经济学奖。1991年，Peters [4] 提出分形市场概念后，研究者们开始使用分数布朗运动(Fractional Brownian Motion)研究期权的定价。Elliott和Hoek [5] 研究了Hurst指数在 $H\in \left(0,1\right)$ 情况下的分数布朗运动。

随着金融市场的不断发展和完善，涌现出了各式各样的变异期权，重置期权是一种依赖于路径的变异期权，即当原生资产价格达到某一预先给定的水平时，按照规定可以重新设置期权的敲定价格，以便使得投资者可以有更多的获利机会，亚式期权也是一种依赖于路径的新型期权，它的收益依赖于整个期权有效期内标的资产所经历的价格平均值，这里所指的平均值包括算术平均值和几何平均值，而本文结合这两种期权，利用等价鞅方法，给出了在分数布朗运动下，几何平均亚式重置期权的定价公式。

2. 预备知识

定义1 [6] ：(Hurst指数)Hurst参数为 $H\in \left(0,1\right)$ 的分数布朗运动为一个连续Gaussian过程且满足

1) $E\left[B_H\left(t\right)\right]=0$

2) $E\left[B_H\left(t\right)B_H\left(s\right)\right]=\frac{1}{2}\left\{{\left|t\right|}^{2H}+{\left|s\right|}^{2H}-{\left|t-s\right|}^{2H}\right\}$

当 $B_H\left(0\right)=0$ ， $H=\frac{1}{2}$ ， $B_H\left(t\right)$ 为标准布朗运动。

设在概率空间 $\left(\text{Ω},F,P\right)$ 下的两种资产——风险资产 $S_t$ 和无风险资产 $B_t$ ，其价格满足

$\text{d}S\left(t\right)=u\left(t\right)S\left(t\right)\text{d}\left(t\right)+\sigma \left(t\right)S\left(t\right)\text{d}{B}_H(t)$

$\text{d}B\left(t\right)=r\left(t\right)B\left(t\right)\text{d}t$

其中 $r\left(t\right)$ 是无风险利率， $u\left(t\right)$ 是标的资产t时刻的瞬时收益率， $\sigma \left(t\right)$ 是标的资产t时刻的瞬时波动率，为方便计算 $r\left(t\right)=r$ ， $\sigma \left(t\right)=\sigma$ 均为非零常数，可知在风险测度Q下，满足 $B_H\left(t\right)=B_t\left(H\right)-\frac{r-u}{\sigma }t$ 是概率测度Q下的分数布朗运动 [7] ，则有下式

$\text{d}S\left(t\right)=r\left(t\right)S\left(t\right)\text{d}\left(t\right)+\sigma \left(t\right)S\left(t\right)\text{d}{B}_H\left(t\right)$ (3)

则上式的解为 [8]

$S\left(T\right)=S\left(0\right)\exp \left\{rT+\sigma B_H\left(T\right)-\frac{1}{2}{\sigma }^2{T}^{2H}\right\}$ (4)

3. 分数布朗运动下的亚式重置期权定价

定义2.1 设期权的敲定价格为K， $J=\exp \left\{\frac{1}{T}{\displaystyle {\int }_0^T\ln S\left(u\right)\text{d}u}\right\}$ 表示到时间T的股票价格的几何平均值，则分数布朗运动下的亚式重置看涨期权在到期日为T的收益为

$V\left(S,J,T\right)=\{\begin{array}{l}{S}_T-J,S_T\ge J,J<K.\\ S_T-K,S_T>K,J\ge K.\end{array}$

定理2.1 标的资产价格在Black-Scholes模型下，期权的敲定价格为K，到期日为T的分数布朗运动下的亚式重置看涨期权的价格为

$C\left(S,K,t\right)=S_{0}N\left(d_3,d_4;\rho \right)-K{\text{e}}^{-rT}N\left(d_1,d_2;\rho \right)+S_{0}N\left(d_5\right)N\left(d_6\right)-{\text{e}}^{u_1+\frac{{\sigma }_Y^2}{2}-rT}N\left(d_7\right)N(d8)$

其中 $d_1=\frac{\ln \frac{S_0}{K}+\frac{1}{2}rT-\frac{{\sigma }^2{T}^{2H}}{2\left(2H+1\right)}}{\sigma {\sigma }_1}$ ， $d_2=\frac{\ln \frac{S_0}{K}+rT-\frac{{\sigma }^2{T}^{2H}}{2}}{\sigma {\sigma }_2}$ ， $d_3=d_1+\sigma {\sigma }_2$ ， $d_4=d_2+\rho \sigma {\sigma }_2$ ， $d_5=\frac{\ln \frac{K}{S_0}-\frac{1}{2}rT-\frac{{\sigma }^2{T}^{2H}}{2\left(2H+1\right)}}{\sigma {\sigma }_1}$ ， $d_6=\frac{\frac{1}{2}rT+\frac{{\sigma }^{2}H{T}^{2H}}{2H+1}}{\sigma {\sigma }_3}$ ， $d_7=\frac{\frac{1}{2}rT-\frac{{\sigma }^{2}H{T}^{2H}}{2H+1}}{\sigma {\sigma }_3}$ ，， ${\sigma }_1^2=\frac{T^{2H}}{2\left(H+1\right)}$ ， ${\sigma }_2^2=T^{2H}$ ， ${\sigma }_3^2=\frac{\left(2H+3\right)T^{2H}}{2\left(H+1\right)}$ ， $\rho =\frac{\sqrt{2\left(H+1\right)}}{2}$ ， $u_1=\ln S_0+rT-\frac{{\sigma }^2{T}^{2H}}{2\left(2H+1\right)}$ ， ${\sigma }_Y^2=\frac{{\sigma }^2{T}^{2H}}{2\left(H+1\right)}$ 。

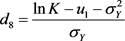$\rho$ 是 $\sigma B_H\left(T\right)$ 和 $\frac{\sigma }{T}{\displaystyle {\int }_0^T{B}_H\left(u\right)\text{d}u}$ 的相关系数。

证明：在风险中性下，亚式看涨重置期权在t时刻的价格为 [9]

$\begin{array}{c}C\left(S,K,t\right)=E_t\left({\text{e}}^{-r\left(T-t\right)}\left(S_T-K\right)1_{\left(J\ge K,S_T>K\right)}\right)+E\left({\text{e}}^{-r\left(T-t\right)}\left(S_T-J\right)1_{\left(J<K,S_T\ge J\right)}\right)\\ =I_1-I_2+I_3-I_4\end{array}$ .

由于 $J=\exp \left\{\frac{1}{T}{\displaystyle {\int }_0^T\ln S\left(u\right)\text{d}u}\right\}=S_0\exp \left\{\frac{1}{2}rT-\frac{{\sigma }^2{T}^{2H}}{2\left(2H+1\right)}+\frac{\sigma }{T}{\displaystyle {\int }_0^T{B}_H\left(u\right)\text{d}u}\right\}$ 。

所以有

$I_1=E_t\left({\text{e}}^{-rT}{S}_T{1}_{\left(S_T>K,J\ge K\right)}\right)=E_t\left(S_0\exp \left(\sigma B_H\left(T\right)-\frac{1}{2}{\sigma }^2{T}^{2H}\right)1_A\right)$

$A=\left\{\ln J\ge \ln K,\ln S_T>\ln K\right\}=\left\{-\frac{\frac{\sigma }{T}{\displaystyle {\int }_0^T{B}_H\left(u\right)\text{d}u}}{\sigma {\sigma }_1}<d_1,-\frac{\sigma B_H\left(T\right)}{\sigma {\sigma }_2}\le d_2\right\}$ .

因为

$\rho =\text{corr}\left(\sigma B_H\left(T\right),\frac{\sigma }{T}{\displaystyle {\int }_0^T{B}_H\left(u\right)\text{d}u}\right)=\frac{\mathrm{cov}\left(\sigma B_H\left(T\right),\frac{\sigma }{T}{\displaystyle {\int }_0^T{B}_H\left(u\right)\text{d}u}\right)}{\sqrt{\mathrm{var}\left(\sigma B_H\left(T\right)\right)\mathrm{var}\left(\frac{\sigma }{T}{\displaystyle {\int }_0^T{B}_H\left(u\right)\text{d}u}\right)}}=\frac{\sqrt{2\left(H+1\right)}}{2}$ .

则 [10]

$I_1=E_t\left({\text{e}}^{-rT}{S}_T{1}_A\right)=S_0\exp \left\{-\frac{1}{2}{\sigma }^2{T}^{2H}\right\}$

${\displaystyle {\int }_{-\infty }^{d_1}{\displaystyle {\int }_{-\infty }^{d_2}\frac{1}{\sqrt{2\pi \left(1-{\rho }^2\right){\sigma }_1{\sigma }_2}}\exp \left\{-\frac{{\left(\frac{x}{{\sigma }_1}\right)}^2-\frac{2\rho xy}{{\sigma }_1{\sigma }_2}+{\left(\frac{y}{{\sigma }_2}\right)}^2}{2\left(1-{\rho }^2\right)}\right\}\exp \sigma y\text{d}x\text{d}y}}$ .

作变换 $\{\begin{array}{l}\frac{x}{{\sigma }_1}-\rho \sigma {\sigma }_2=z_1\\ \frac{y}{{\sigma }_2}-\sigma {\sigma }_2=z_2\end{array}$ 代入上式积分中，得

$I_1=S_0{\displaystyle {\int }_{-\infty }^{d_3}{\displaystyle {\int }_{-\infty }^{d_4}\frac{1}{2\pi \sqrt{\left(1-{\rho }^2\right)}}\exp \left\{-\frac{z_1^2-2\rho z_1{z}_2+z_2^2}{2\left(1-{\rho }^2\right)}\right\}\text{d}{z}_1\text{d}{z}_2}}=S_{0}N\left(d_3,d_4;\rho \right)$ .

同理可得

$I_2=E_t\left({\text{e}}^{-rT}K{1}_{\left(J\ge K,S_T>K\right)}\right)=K{\text{e}}^{-rT}{E}_t\left(1_A\right)=K{\text{e}}^{-rT}N\left(d_1,d_2;\rho \right)$ .

计算 $I_3$ ，构造测度R，由Girsanov定理， $\widetilde{B_H}\left(t\right)=B_H\left(t\right)-\sigma t^{2H}$ 且 $\widetilde{B_H}\left(t\right)$ 在R下仍为分数布朗运动，且该测度下标的资产价格为：

$S\left(T\right)=S\left(0\right)\exp \left\{rT+\sigma \widetilde{B_H}\left(T\right)+\frac{1}{2}{\sigma }^2{T}^{2H}\right\}$

从而

$\begin{array}{c}{I}_3=E_t\left({\text{e}}^{-rT}{S}_T{1}_{\left(J<K,S_T\ge J\right)}\right)=S_0{E}_t\left({\text{e}}^{-rT}\frac{S_T}{S_0}{1}_{\left(J<K,S_T\ge J\right)}\right)=S_0{Q}_R\left(J<K,S_T\ge J\right)\\ =S_0{Q}_R\left(\frac{\frac{\sigma }{T}{\displaystyle {\int }_0^T\widetilde{B_H}\left(u\right)\text{d}u}}{\sigma {\sigma }_1}<\frac{\ln \frac{K}{S_0}-\frac{1}{2}rT-\frac{{\sigma }^2{T}^{2H}}{2\left(2H+1\right)}}{\sigma {\sigma }_1},-\frac{\sigma \widetilde{B_H}\left(T\right)-\frac{\sigma }{T}{\displaystyle {\int }_0^T\widetilde{B_H}\left(u\right)\text{d}u}}{\sigma {\sigma }_3}\le \frac{\frac{1}{2}rT+\frac{{\sigma }^{2}H{T}^{2H}}{2H+1}}{\sigma {\sigma }_3}\right)\\ =S_{0}N\left(d_5\right)N\left(d_6\right)\end{array}$ .

因为

$\begin{array}{l}{I}_4=E_t\left({\text{e}}^{-rT}J{1}_{\left(J<K,S_T\ge J\right)}\right)\\ ={\text{e}}^{-rT}{E}_Q\left(J{1}_{\left(J<K\right)}\right)P\left(S_T\ge J\right)={\text{e}}^{-rT}{E}_Q\left(J{1}_{\left(J<K\right)}\right)N\left(d_7\right)\end{array}$ .

又有

$E_Q\left(J{1}_{\left(J<K\right)}\right)={\displaystyle {\int }_{-\infty }^{K}x{f}_J\left(x\right)\text{d}x}={\displaystyle {\int }_{-\infty }^{\ln K}{\text{e}}^y{f}_J\left({\text{e}}^y\right){\text{e}}^y\text{d}y}$ .

其中 $f_J$ 是在测度Q下的密度函数，在测度Q下 $$ 。

可知

$\begin{array}{c}{E}_Q\left(J{1}_{\left(J<K\right)}\right)={\displaystyle {\int }_{-\infty }^{\ln K}{\text{e}}^y{f}_J\left({\text{e}}^y\right){\text{e}}^y\text{d}y}\\ ={\displaystyle {\int }_{-\infty }^{\ln K}\frac{1}{\sqrt{2\text{π}}{\sigma }_1}\exp \left\{-\frac{{\left(y-u_1\right)}^2}{2{\sigma }_1{}^2}\right\}{\text{e}}^y\text{d}y}\\ ={\text{e}}^{u_1+\frac{{\sigma }_Y^2}{2}}N\left(d_8\right)\end{array}$ .

所以

$I_4=E_t\left({\text{e}}^{-rT}J{1}_{\left(J<K,S_T\ge J\right)}\right)={\text{e}}^{u_1+\frac{{\sigma }_Y^2}{2}-rT}N\left(d_7\right)N\left(d_8\right)$ .

综合 $I_1,I_2,I_3,I_4$ 可得到最终结果，证毕。

4. 数值结果与分析

下面我们考虑一个例子，假设执行价格K = 100，无风险利率r = 0.1，到期日T = 2 (年)，利用MATLAB程序，可得到如下表格(表1，表2)。

表1. 不同H指数时分数布朗运动下亚式期权和亚式重置期权的价格

表2. 不同H指数时分数布朗运动下亚式期权和亚式重置期权的价格

从表1我们可以看出分数布朗运动下亚式重置看涨期权的价格比分数布朗运动下亚式看涨期权价格略高。投资者多了一次重置的权利，期权的价格自然就比不重置的期权价格高，而且随着股票初始价格的增加，两种期权的价格也越来越接近。考察Hurst指数取不同值时，分数布朗运动下的亚式重置看涨期权和亚式看涨期权的数值结果，随着H指数的增大，期权价格也随之增大。当固定H指数时，随着股票波动率的增大，两种期权的价格也增大。

5. 结论

本文在分数布朗运动环境下，以亚式几何平均重置期权为例子，通过等价鞅方法得到其期权定价公式，并分析了不同Hurst指数下亚式重置期权以及亚式期权的价格，对比两种期权的价格，我们可以得出分数布朗运动下几何平均亚式重置期权比分数布朗运动下几何平均亚式期权的价格高，也就是说其获利的机会更多。本文仅考虑了分数布朗运动下的几何平均亚式重置期权的定价，对于分数布朗运动下的算术平均亚式重置期权的定价情况有待于进一步的研究。

文章引用

程斯吉. 分数布朗运动下的亚式重置期权定价
Fractional Brownian Motion under the Asian Reset Option Pricing[J]. 理论数学, 2019, 09(04): 551-556. https://doi.org/10.12677/PM.2019.94073

参考文献