Pure Mathematics
Vol.
09
No.
07
(
2019
), Article ID:
32339
,
7
pages
10.12677/PM.2019.97109
The λ-Radical and Regular Radical in Normal Classes of Complete Pointwise Algebra
Zongwen Yang,
Department of Mathematics, Yunnan University, Kunming Yunnan
Received: Aug. 29th, 2019; accepted: Sep. 18th, 2019; published: Sep. 25th, 2019

ABSTRACT
Two equivalent conditions of radical class are given, and two kinds of algebras of λ-algebra and regular algebra in normal class of pointwise complete algebra are defined. It is proved that class λ of λ-algebra and class ν of regular algebras are all radical classes.
Keywords:Normal Classes of Complete Pointwise Algebras, λ-Algebras, λ-Radical, Regular Algebras, Regular Radical
点态化完备代数正规类中的λ-根和正则根
杨宗文,何青海
云南大学,数学系,云南 昆明
收稿日期:2019年8月29日;录用日期:2019年9月18日;发布日期:2019年9月25日

摘 要
给出了根类的判别的2组等价条件,定义了点态化完备代数正规类中的λ-代数与正则代数2类代数,并证明了λ-代数类λ与正则代数类ν都是根类。
关键词 :点态化完备代数正规类,λ-代数,λ-根,正则代数,正则根

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
环及其它代数系统根理论的统一研究促使一般代数正规类根理论的建立 [1] - [15] ,为了能在一般代数正规类中进一步统一的研究根性质,文献 [16] - [23] 分别引入了可积代数正规类、完备代数正规类,对特殊根等进行了研究,并对一类特殊的半环——大半环(可做单侧减法的半环)建立了相应的根理论;文献 [24] [25] 对完备代数正规类进行了点态化,研究了点态化完备代数正规类中的亚直既约代数类确定的上根——反单根、遗传幂等根、补根、对偶根、子幂等根、诣零根的结构性质。
本文在文献 [24] [25] 建立的点态化完备代数正规类概念基础上,进一步加强了点态化完备代数正规类的公理,给出了根类的判别的2组等价条件,研究了点态化完备代数正规类中的λ-根和正则根性质。
2. 预备知识及基本引理
点态化完备代数正规类的相关概念及性质参见文献 [24] [25] 。
定义2.1 [12] : 是一个代数类, ,如果R满足:
a) ,,如果a∈R,则 (即R商闭);
b) ,a有一个最大的R-理想(记为R(a)),称a的R-根;
c) ,有 。
则称R为 中的一个根类,简称根。
定义2.2 [12] : 是一个代数类, 是一个根类, 中代数类 称为R的半单类,PR中元素称为R-半单代数。
引理2.3 [15] : 是一个完备代数正规类,则:
1) 如果 ,则 ,特别 ;
2) 如果 ,则 ;
3) n是正整数,如果 ,则 。
引理2.4 [13] [14] : 是一个完备代数正规类,R为 中的一个根类, ,。如果 ,则 。
引理2.5 [15] : 是一个完备代数正规类,K为 的一个子类,K中每个代数的理想都在K中(即K对理想封闭)。则 是一个根类(称由K确定的上根,记为UK),且 。进一步有:如果 是一个根类,且 ,则 ,记为根类 。
引理2.6 [15] : 是一个完备代数正规类, ,,, 是a的包含k的最小理想。则 ,且 。
引理2.7 [24] [25] :设 是一个非零代数, 是完备代数正规类中 到 的映射。则 有:
当且仅当 。
引理2.8 [24] [25] :设 是一个非零代数, 是完备代数正规类中 到 的映射, ,。则:
1) 存在a的一个最大的理想 ,使得 ;
2) 分别存在a的一个最小的在 下的像包含t的子代数 、右理想 、左理想 、理想 ,且
,,
,,
分别称t生成的主子代数 、主右理想 、主左理想 及主理想 ;
3) 分别存在a的一个最小的 下的像包含A的子代数 、右理想 、左理想 、理想 ,且
,,
,,
分别称A生成的子代数 、右理想 、左理想 及理想 ;
4) , ; , ; , ; , ;
5) ,则 当且仅当 。
注1 引理2.8中性质(5)在文献 [24] [25] 中由于笔误写成了“ 当且仅当 ”。
根类的判别经常可用以下2组条件。
定理2.9: 是一个代数类, ,R为 中的一个根类 R满足以下3个条件:
a) ,,如果 ,则 (即R商闭);
b) ,a有一个最大的R-理想(记为R(a));
) ,,如果 ,则有 (称R扩张闭)。
证明 “ ”此处只需证明由条件(a),(b),(c)可推出条件( )。 ,,,如果 ,则由条件(b),(c)有 ,。又由条件(b)有 ,所以 ,由 及性质(a)有 ,即 ,矛盾。所以 ,即条件( )成立;
“ ”此处只需证明由条件(a),(b),( )可推出条件(c)。 ,有 ,,,则由条件( )及i/R(a), 有 ,即i是a的R-理想,由条件(b)有 ,所以 ,即条件(c)成立。证毕。
定理2.10: 是一个代数类, ,R为 中的一个根类 R满足以下3个条件:
a) ,,如果 ,则 (即R商闭);
) ,如果 是a的R-理想升链(即 ),则理想 (称R有归纳性质);
) ,,如果 ,则有 (称R扩张闭)。
证明 “ ”此处只需证明由条件(a),(b),( )可推出条件( )。 ,由条件(a),(b),(c)有
。如果 是a的R-理想升链,取 ,从而 是b的R-理想升链,则 ,即 ,故条件( )成立;
“ ”此处只需证明由条件(a),( ),( )可推出条件(b)。 ,由条件( )及Zorn引理a有极大R-理想b。对a的任意R-理想k,考虑 ,,从而由条件( )有 ,
由b的极大性有 ,所以 是a的最大R-理想,即条件(b)成立。证毕。
3. 点态化完备代数正规类
是一个完备代数正规类, 是完备代数正规类中 到 的映射 [24] [25] 。
则有:
引理3.1: 设0是 的零代数,则 ,有 。
证明 ,,有 ,故 ,所以 。证毕。
引理3.2: 设 , 是a的零子代数, 是a的任意子代数,单点集 ,则:
1) , ;
2) 。
今后都记为 ,。
证明 1) ,,所以 ,即 。 ,所以 ,即 ;
2)此处只需证明 。因为 ,即0是a的使得 一个子代数,故
。证毕。
引理3.3: 设 ,,则 当且仅当 。
证明 由引理3.2,此处只需证明 时有 。如果 ,说明 有2个以上元素,从而不是单点集,因此 ,矛盾。所以 。证毕。
在 定义中取 ,有:
引理3.4: 设 ,,满射 是完备代数正规类中定义的映射 [24] [25] , ,则 。
引理3.5: 设
,,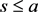 ,则
。
,则
。
证明 由 定义条件(4),有 。证毕。
设 是一个完备代数正规类, ,非空集 和一个单射 如前定义。如果对正整数n, ,存在一个 ,,使得 ,,, ;对正整数n, 的非空有限子集或可数子集A,存在有限子集 ,,使得 ,,,,则称 是一个点态化完备代数正规类。 ,称x是a的一个点。
设S是一个非空集,S上的点乘积定义为S上一个满足以下条件的二元运算' ':
1) ,都有 ( 记为xy);
2) ,有 (记为xyz);
3) 存在唯一的单点 ( 也记为0),满足: ,有 。
S是一个带乘积的集合, ,则定义: 。
为了更方便的刻画幂零性,对带点乘积的点态化完备代数正规类进行一点加强:
定义3.6: 设 是一个点态化完备代数正规类,如果 满足点乘积公理:
A9 (点乘积公理). , 是一个带乘积的集合。
且 ,,,正整数n, ,,,对满射 ,满足 ,且 ,则存在 ( ),使得
,
,。
则称 是一个带点乘积的点态化完备代数正规类,简称点态化完备代数正规类。
注2 本文对点态化完备代数正规类乘积性质相对文献 [24] [25] 进行了一些加强。
文中后面所称点态化完备代数正规类都是指带点乘积的点态化完备代数正规类。
根据点态化完备代数正规类定义可知,点态化完备代数正规类是完备代数正规类及可积代数正规类,从而参考文献中关于完备代数正规类及可积代数正规类的结论在点态化完备代数正规类中都成立。从而结合环类R和大半环类SB都是点态化完备代数正规类。
引理3.7: 设 ,。
1) ,从而 ,有 ;
2) n是正整数,则 , ;
3) x是幂零元当且仅当存在正整数n,使得 。
证明 1) 因为 ,所以 ;
2) n = 1时有 , ;n = 2时有 ,所以 ;又因为 ,所以 。即n = 1,2时结论成立。
设 时 , 结论成立,则n=k时有
,
从而 ;又因为 ,所以 。即n = k时结论(2)成立。
根据数学归纳法,(2)中结论对所有正整数n成立。
3) x是幂零元,则存在正整数n,使得 ,即 ,从而 。
若存在正整数n,使得 ,则 ,即x是幂零元。证毕。
4. 点态化完备代数正规类中的λ-根与正则根
是一个点态化完备代数正规类。
定义4.1: ,,设 ,。
1) ,如果有 ,则称x是a的一个λ-元素;
2) 如果 ,x是a的λ-元素,则称a是一个λ-代数;
3) ,如果有 ,则称x是a的一个正则元素;
4) 如果 ,x是a的正则元素,则称a是一个正则代数。
记所有λ-代数的类为λ,记所有正则代数的类为ν。
定理4.1: λ-代数类λ是一个根类。
证明:1) 设 ,,,对满射 ,存在 ,。由 ,有 ,所以 ,从而x是a/i的λ-元素,a/i是λ-代数,代数类λ对商闭。
2) ,如果 是a的λ-理想升链, ,故存在μ,使得 ,因此 ,即 是λ-代数,代数类λ有归纳性质。
3) ,,如果 。 ,,因此 ,所以有 ,使得 ,。因为 ,,所以 ,故 ,即 ,代数类λ扩张闭。
根据定理2.10,代数类λ是一个根类。证毕。
λ-代数类确定的根类λ称λ-根。
定理4.2:正则代数类ν是一个根类。
证明:1) 设 ,,,对满射 ,存在 ,。由 ,有 ,所以 ,从而x是a/i的正则元素,a/i是正则代数,代数类ν对商闭。
2) ,如果 是a的ν-理想升链, ,故存在μ,使得 ,因此 ,即 是正则代数,代数类ν有归纳性质。
3) ,,如果 。 , ,因此 ,所以有 ,使得 ,。因为 ,,所以 ,故 ,即 ,代数类ν扩张闭。
根据定理2.10,代数类ν是一个根类。证毕。
正则代数类确定的根类ν称正则根。
5. 小结
本文给出了根类的判别的2组等价条件,定义了λ-代数与正则代数2类代数,并证明了λ-代数类λ与正则代数类ν都是根类。
基金项目
国家自然科学基金(11261067)。
文章引用
杨宗文,何青海. 点态化完备代数正规类中的λ-根和正则根
The λ-Radical and Regular Radical in Normal Classes of Complete Pointwise Algebra[J]. 理论数学, 2019, 09(07): 836-842. https://doi.org/10.12677/PM.2019.97109
参考文献
- 1. Száse, F.A. (1981) Radicals of Rings. John Wiley & Sons, New York.
- 2. Gardner, B.J. and Wiegandt, R. (2004) Radical Theory of Rings. Marcel Dekker, New York and Basel.
https://doi.org/10.1201/9780203913352 - 3. Beidar, K.I., Fong, Y. and Ke, W.-F. (1998) On Complemented Radicals. Journal of Algebra, 201, 328-356.
https://doi.org/10.1201/9780203913352 - 4. Tumurbat, S. and Zand, H. (2001) Hereditariness, Strongness and Relationship between Brown-McCoy and Behrens radicals. Contributions to Algebra and Geometry, 42, 275-280.
- 5. 蔡传仁. 对偶根和F A SZASZ的问题21[J]. 数学学报(中文版), 1989, 32(3): 394-400.
- 6. 蔡传仁. 半遗传根的一个特征性质[J]. 数学研究与评论, 1991, 11(1): 9-12.
- 7. 谢邦杰. 关于周期环与Jacobson环的几个定理[J]. 数学研究与评论, 1982, 2(2): 11-13.
- 8. 于宪君.关于FA, δ-环与广义周期环的几个定理[J].数学研究与评论, 1988, 8(3): 341-345.
- 9. 胡小美. 几类与Jacbson根相关环的研究[D]: [硕士学位论文]. 杭州: 杭州师范大学, 2017.
- 10. 于宪君, 朱捷. 关于周期环的几个定理[J]. 黑龙江大学自然科学学报, 2004, 21(3): 20-22.
- 11. 杜现昆, 齐毅. 周期环的刻划[J]. 吉林大学自然科学学报, 2001, 39(3): 29-31.
- 12. Puczylowski, E.R. (1993) On General Theory of Radicals. Algebra Universalis, 39, 53-60.
https://doi.org/10.1007/BF01196549 - 13. Wang, Y. and Zhang, A. (2002) Radicals and Semisimple Classes of the Class of Algebras. Journal of Anshan Normal University, 4, 5-10.
- 14. 任艳丽, 王尧. 代数正规类中的遗传根与强半单根[J]. 数学研究与评论, 2004, 24(4): 597-602.
- 15. Yang, Z.W. (2006)The Upper Radical Classes of the Class of Algebras. Journal of Yunnan Uni-versity (Natural Sciences Edition), 28, 8-11.
- 16. Yang, Z.W. and Pan, J.M. (2008) The Supernilpotent Radical, Special Radical and Bear Radical in Normal Classes of Product Algebras. Southeast Asian Bulletin of Mathematics, 32, 181-192.
- 17. Yang, Z.W. and Pan, J.M. (2010) The Radicals and Likemodules in Normal Classes of Complete Alagebras. Southeast Asian Bulletin of Mathematics , 34, 377-386.
- 18. 杨宗文, 杨柱元. 完备代数正规类的根与右理想[J]. 昆明理工大学学报(理工版), 2006, 31(3): 112-116+120.
- 19. 杨宗文, 杨柱元. 子环的和与积[J]. 云南大学学报(自然科学版), 2007, 29(4): 335-338.
- 20. 杨宗文, 杨柱元, 李友宝. 大半环子半环的和与积[J]. 昆明理工大学学报(理工版), 2007, 32(6): 113-118.
- 21. 杨宗文, 杨柱元, 李友宝. 可积代数正规类中半素代数类及半素一致代数类确定的上根[J]. 数学理论与应用, 2008, 28(4): 71-75.
- 22. Yang, Z.W., Yang Z.Y. and Li, Y.B. (2010) The General Radicals Theory of the Big Semirings. Southeast Asian Bulletin of Mathematics, 34, 1149-1167.
- 23. Yang, Z.W. and Yang Z.Y. (2011) The Semihereditary and Semisupernilpotent Radicals in Normal Classes of Product Algebras. Southeast Asian Bulletin of Mathematics, 35, 891-902.
- 24. 杨宗文, 何青海. 点态化完备代数正规类中的亚直既约代数类[J]. 理论数学, 2018, 8(5): 546-554.
- 25. 杨宗文, 何青海. 点态化完备代数正规类中的遗传幂等根、补根、对偶根、子幂等根及诣零根[J]. 理论数学, 2018, 8(6): 712-722.