Pure Mathematics
Vol.
09
No.
08
(
2019
), Article ID:
32626
,
21
pages
10.12677/PM.2019.98120
The Proof of 15 Projective Spheres between Orthogonal Four Spheres and Algorithm of Distance Formula
—Application of Pythagorean Theorem of Four Dimensional Volume (Formula (3))
Guowei Cai
Shanghai Huimei Property Co. Ltd., Shanghai

Received: Sep. 29th, 2019; accepted: Oct. 17th, 2019; published: Oct. 24th, 2019

ABSTRACT
A vertical tetrahedron consisting of four orthogonal sphere centers from one sphere to four spheres has 15 projective spheres of four points, six lines, four planes and one body. The 105 spacing between these 15 projective spheres can be calculated by the distance formula of two coordinates. It can also get rid of coordinates and calculate directly by using the formula of center of projective sphere spacing. It is also proved that the distance between the homomorphic center of gravity and the vertical center is the square variance of the radius of two spheres.
Keywords:Volume Pythagorean Theorem, Application, Orthocentric Tetrahedron, Projective Sphere, Spacing Formula, Algorithms
证明正交四球间15个垂心球及距离公式的 算法
——四维体积勾股定理的应用(公式(三))
蔡国伟
上海汇美房产有限公司,上海
收稿日期:2019年9月

29日;录用日期:2019年10月17日;发布日期:2019年10月24日

摘 要
1球至4球正交球心构成的垂心四面体,存在4点、6线、4面、1体15个垂心球,这15个垂心球间的105个间距,除了可用2点坐标的距离公式计算外;还可以摆脱坐标直接利用垂心球间距公式计算。并且证明了同态重心与垂心间距为2球半径的平方差。
关键词 :体积勾股定理,应用,垂心四面体,垂心球,间距公式,算法

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
4球正交,球心间的垂心四面体构成的4个球心点(球)、6个两球间连线(勾股定理)、4个3球心所围面(面积勾股定理 [1] )、1个4球心所围体(四维体积勾股定理 [2] )均有各自的垂心。那么这15个垂心间的间距除了用2点坐标的距离公式计算外,是否能摆脱坐标,直接用垂心球距离公式计算呢?垂心球与重心球 [3] 间关系如何?
2. 垂心球球心间存在间距公式的证明
4球正交,根据勾股4态 [3],以及垂心四面体垂心的性质 [4] 共有15点垂心球球心(4点与球心共点、6点为2球心间连线的射影点、4点为3球心所围面的垂心、1点4球心所围体的垂心),15个垂心球间距数量根据等差求和公式为:
共有105个间距,这105个间距可摆脱坐标,直接用同构的垂心球球心间距公式计算:
2.1. 3个公式(2点垂心距离;同态重心与垂心间距;垂心球半径)
2.1.1. 正交4球间15点垂心任意2点距离公式
定义:正交4球心间勾股4态存在15点垂心,任意2垂心间距的平方,等于2垂心球半径的平方和与2倍的2垂心球的平方积与2垂心球交集垂心球平方的倒数积之差。其公式为:
(1)
(这里:
为15点中任意2点垂心距离的平方,
为2垂心球的平方和,
为交集垂心球的平方的倒数;下标:H为垂心,
)
2.1.2. 正交4球间15组垂心与重心的间距公式
定义:正交4球心间勾股4态存在15点垂心和15个重心,同态的15组垂心与重心的间距为:相对应的重心球半径 [5] 与垂心球半径的平方差。其公式为:
(2)
(这里:
为同态15组重心与垂心间任意一组间距的平方;
为同态重心球半径与垂心球半径的平方差,下标:G为重心、H为垂心,
)
2.1.3. 一至四维同构的垂心球半径平方公式
定义:一至四维垂心球的平方等于并集球球心间无系数的场方程 [3] 的倒数与并集一维球半径平方积。其公式为:
(3)
这里下标
;
;上标
。
例:
· 4个一维垂心球:
因球心与垂心共点,4个一维垂心球平方分别为:
;
· 6个二维垂心球:
6个二维垂心至两端相关球面距离的乘积为:
· 4个三维垂心球:
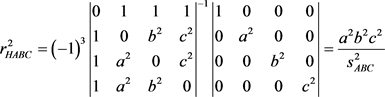
4个三维垂心至3球面2交点距离的乘积为:
,
这里: ,,, (下同)
· 1个四维垂心球,
这里: (下同)
其四维垂心至4组3球面2交点距离距离的乘积为: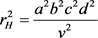 。
。
2.2. 在欧氏空间,建立正交4球间15点垂心,以及8点3球面交点,共23点坐标
建立坐标的目的,主要用于验证公式(1),最终达到摆脱坐标,用垂心球公式计算垂心间距。
2.2.1. 设15点垂心以及8点3球面交点坐标及垂心球半径符号
所设:一至三维垂心坐标(除了H外)见图1,以及垂心球半径见表1。
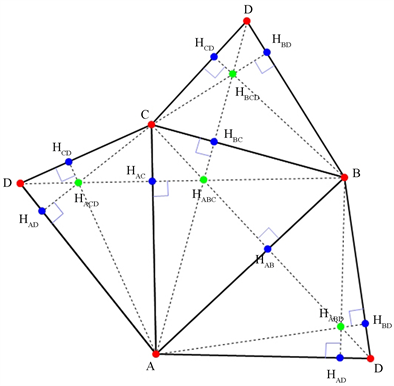
Figure 1. Symbolic expansion of point, line and surface projective coordinates
图1. 点、线、面3态垂心坐标符号展开图
2.2.2. 计算15点垂心坐标和8点球面交点坐标
· 4点一维球垂心坐标,因球的球心与垂心共点。4球心即4垂心
坐标。详见表1。
· 6点二维线垂心坐标计算:
例:计算
坐标。
建立 球心2点直线参数方程为:
球心2点直线参数方程为:
,

Table 1. 15-Point projective coordinates and the square of radius of projective sphere
表1. 15点垂心坐标和对映的垂心球半径的平方
表内:D坐标在第7象限。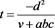 ,
;
;
;
;
。
,
;
;
;
;
。
建立
参数球面联立方程,求参数t为:
将参数t代入上式:
⇒得坐标:
同理:可得其它5点
坐标。详见表1;
· 4点三维面垂心坐标(见表1)计算:(8点3球面交点坐标见表2)
例:计算
和
三点坐标。
根据A,B,C联立3球面方程可得球面2交点,以及2点间中点为该平面的垂心
坐标:
⇒得
,,
式内:
;
;
;
;下同。
(上述3点与过D的垂线共线,近D点的内凹点为
,远D点的外凸点为 ,坐标
)
,坐标
)
同理可得其它9点
坐标。详见表1。
· 球心构成的垂心四面体的垂心坐标计算:设:H坐标为:
建立
2点直线参数方程:

Table 2. The projective spheres at the intersection point of eight spheres are all zero relative to the projective spheres at the intersection of three sphere centers
表2. 8点3球面交点坐标,相对于3球心交平面的一至三维垂心球,球面8交点的垂心球均为零
表内:下标:−内凹为负,+外凸为正;
,。
, (4)
这里:
;
;下同
建立
2点直线参数方程:
, (5)
2参数方程,公式(4)与公式(5)之差为公式(6),求参数
。
⇒得
(6)
再将求得的参数
代回公式(3);
或将参数
代回公式(5),
均得相同的垂心坐标:
。
2.2.3. 根据正交4球心勾股4态 [3] (点、线、面、体)的垂心代数坐标及对应的垂心球半径的平方列表
根据正交4球心构成的垂心四面体性质 [4],计算得出的(点、线、面、体)的15点垂心垂心坐标及对映的垂心球半径平方列表1;以及8点3球面交点坐标均为8原点列表2如下。
3. 验证公式(1)、公式(2)
根据上述坐标,用2点坐标的距离公式验证垂心球距离公式(1)如下:
3.1. 一维至四维垂心自身距离为零
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
3.2. 任意一维与对平面7点因无交集球,其倒数为零,距离的平方为2垂心球半径的平方和
以D点与对平面
7点距离为例:
3.2.1. D点与对平面3个一维垂心间距平方
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
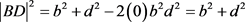 (垂心球距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
3.2.2. D点与对平面3个二维垂心间距平方
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
3.2.3. D点与对平面1个三维垂心间距平方
(2点坐标距离公式)
(垂心球距离公式)
3.3. 任意一维与除了对平面7点外其它7点垂心距离的平方
以D点与除对平面其它7点
间距平方为:
3.3.1. D点与除对平面外,另3个二维垂心间距平方
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
3.3.2. D点与除对平面外,另3个三维垂心间距平方
(2点坐标距离公式)
(垂心球距离公式)
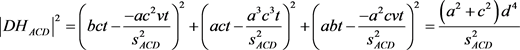 (2点坐标距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
3.3.3. D点与除对平面1个四维垂心间距平方
(2点坐标距离公式)
(垂心球距离公式)
同理可得:A点、B点、C点与其它14点距离(略)。
3.4. 验证任意二维与除了4点一维外的10点距离的平方
以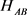 对
对
3.4.1. HAB点与对棱1个二维垂心HCD间距平方,因交集球倒数为零,距离的平方为两球半径的平方
与
因对棱无交集球,其距离的平方为2垂心球半径的平方和
(2点坐标距离公式)
(垂心球距离公式)
3.4.2. HAB点与其它4个旁棱二维垂心间距平方
(2点坐标距离公式)
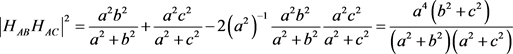 (垂心球距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
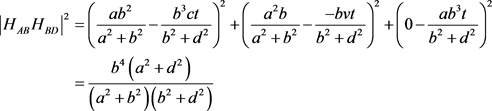 (2点坐标距离公式)
(2点坐标距离公式)
(垂心球距离公式)
3.4.3. HAB点与4个三维垂心间距平方
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
(2点坐标距离公式)
(垂心球距离公式)
3.4.4. HAB点与1个四维垂心间距平方(任意二维与四维垂心间距均相同)
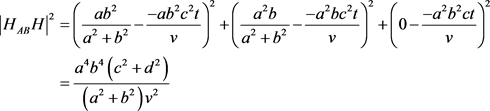 (2点坐标距离公式)
(2点坐标距离公式)
(垂心球距离公式)
同理可得:
点与其它点距离(略)。
3.5. 验证任意三维与四维垂心距离的平方
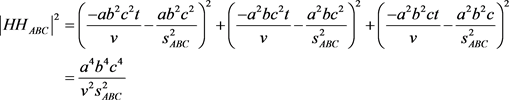 (2点坐标距离公式)
(2点坐标距离公式)
(垂心球距离公式)
同理可得:
点与H点的距离(略)。
3.6. 论4球面均为原点,以及勾股4态的15个垂心球构成的证明, 同时验证8原点垂心球为零公式
正交4球存在4组3球面8交点即为8原点,8原点的垂心球半径均为零,一至四维15个垂心至每组凹凸2原点距离的乘积等于该组垂心球半径的平方;
3.6.1. 一维垂心球:(正交4球面,每球面均处处为原点)
4球心除了对平面外,与相邻3组3球面6交点每组凹凸2点的乘积相同为一维垂心球半径的平方。
例:
(7)
验算:用2点坐标计算距离:
验算:用垂心球公式计算距离:A与原点无交集球
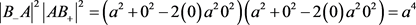
上述验算两边开方,即得公式(7)。
同理可得其余3组一维垂心球等式为:
3.6.2. 二维垂心球:(正交两球形成2正交圆环,圆环处处为原点)
6个二维垂心球,每个垂心各有3组两端的乘积相同为二维垂心球半径的平方。
例:
(8)
验算:用2点坐标计算距离:
验算:用垂心球公式计算距离:
与原点无交集球
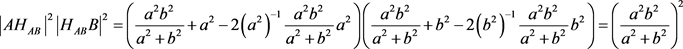
上述验算两边开方,即得公式(8)。
同理可得其余5组二维垂心球等式为:
3.6.3. 三维垂心球:(正交3球面交2点为原点)
4个三维垂心球,每个垂心各有4组两端的乘积相同为三维垂心球半径的平方。
(9)
验算公式(9):
用2点坐标式
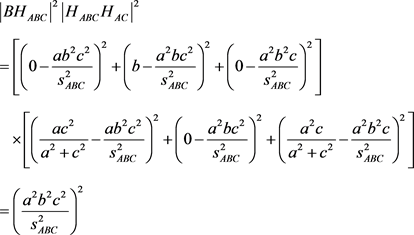
用垂心球距离公式:
上述验算两边开方,得公式(9)
同理可得其余3组三维垂心球等式为:
3.6.4. 四维垂心球:(4组8点正交3球面点为8原点)
(10)
验算1:H至3球面2交点距离的乘积:
用2点距离公式:
用垂心球距离公式:
因8原点均系3球正交原点,8原点垂心球为零适用3维以下,一般四维垂心点不可直接使用。分析
2点间距,因
5点均在过顶点D的垂线上。且:
;
而
两边开方
,
另:
两边开方
这样:
同理:可得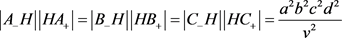 (略)
(略)
验算2:H至球心及其对平面垂心距离的乘积:
两边开方
同理:可得
(略)
通过上述验算:证明了公式(1)成立,同时佐证了勾股四态垂心球的构成。
3.7. 验证公式(2)
用垂心球球心坐标和重心球球心坐标 [3],用2点坐标的距离公式验证同态重心与垂心距离公式(2)即:论勾股四态15个重心球球心与同态的15个垂心球球心间距的平方,为重心球半径的平方与垂心球半径的平方差。
验证如下:
3.7.1. 4组同态一维重心与垂心共点,间距为零
同理可得其余:
,,。
3.7.2. 6组同态二维重心与垂心间距
(2点坐标距离公式)
(2球半径的平方差距离公式)
同理可得其余
二维重心与垂心距离的平方。
3.7.3. 4组同态三维重心与垂心间距
(2点坐标距离公式)
(2球半径的平方差距离公式)
同理可得其余3组
三维重心与垂心距离的平(略)
3.7.4. 1组同态四维重心与垂心间距
(2点距离公式)
(2球半径的平方差距离公式)
通过上述验算:公式(2)成立。
同时也佐证了重心球 [5] 和垂心球半径公式(3)的确立。
4. 总结
通过上述用垂心球计算垂心间距公式、勾股四态一至四维同构的垂心球半径公式、以及同态重心与垂心间距公式的验证。我们得出如下结论:
4.1. 正交4球的各球面均为原点,4组3球面交的8原点,其垂心球或重心球半径均为零
4.1.1. 一维点态球面均为原点
一维点态正交的球面中任意点均为原点,4球面均有无数原点;
4.1.2. 二维线态球面正交圆环为原点
二维线态球面正交圆环任意点均为原点,4球正交球面形成6个正交圆环均有无数原点;
4.1.3. 三维面态球面正交有2个3球面交的原点
三维面态3球正交,有2个3球面正交的原点;
4.1.4. 四维体态正交有8个3球面交的原点,4组球面交点连线交于垂心
四维体态4球正交,有4组3球正交,3球面交8点均为原点;4组球面交点连线相交于垂心。
4.2. 正交4球15个垂心球存在105个垂心间距可分3类
4.2.1. 相间垂心间距为垂心球半径的平方和有25组
正交4球15个垂心中相间的垂心因无交集垂心球,其间距的平方为2垂心球半径的平方和;如:各球心与对平面7点垂心以及对棱二维中点垂心间距平方,均为2垂心球半径的平方和;例:
;
等。
4.2.2. 相邻垂心间距为2垂心球半径的平方差有50组
正交4球15个垂心中相邻的垂心因交集垂心球与低维垂心球半径相同,其间距的平方为低维垂心球半径与高维垂心球半径的平方差;如:四维垂心H与其它14点垂心均相邻,例:
;
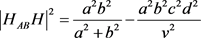 ;
;
4.2.3. 其余非相间相邻的二维、三维垂心间距有30组
剩余的30组非相间也非相邻的垂心间距,套用垂心球计算垂心间距也很方便。例:
;
,
4.3. 正交球垂心间距以及同态重心与垂心间距计算,摆脱了坐标
4.3.1. 勾股4态105种垂心间距可摆脱坐标计算
正交4球勾股4态球心间15点垂心的105间距,以及8点3球面交点与垂心间距,均可摆脱坐标利用公式(1)计算。
4.3.2. 垂心间距公式可摆脱坐标,推广至4球面交8原点至各垂心间距
正交4球勾股4态球面8原点与垂心间距也可利用公式(1), 15点垂心间的105间距,以及8点3球面交点与垂心间距,均可摆脱坐标使用公式(1)计算。
4.3.3. 同态15组重心与垂心间距为两球半径的平方差
同态重心与垂心间距,利用垂心球以及重心球半径,利用公式(2),可直接得出平方差间距。
4.3.4. 垂心球公式可推广至任意有限高维
垂心球公式(3),更可以向任意有限高维拓展。
文章引用
蔡国伟. 证明正交四球间15个垂心球及距离公式的算法——四维体积勾股定理的应用(公式(三))
The Proof of 15 Projective Spheres between Orthogonal Four Spheres and Algorithm of Distance Formula—Application of Pythagorean Theorem of Four Dimensional Volume (Formula (3))[J]. 理论数学, 2019, 09(08): 928-948. https://doi.org/10.12677/PM.2019.98120
参考文献
- 1. 陶杰. 勾股定理的新探索——把勾股定理推广到三维空间[J]. 中等数学, 1983(2): 44.
- 2. 蔡国伟. 体积勾股定理的证明[J]. 理论数学, 2019, 9(6): 723-729.
- 3. 蔡国伟. 论勾股四态、以及正交球心间同构的场方程[J]. 理论数学, 2019, 9(7): 763-770.
- 4. 耿恒考. 四面体的重心与垂心的性质[J]. 数学通报, 2010, 49(10): 55-57.
- 5. 蔡国伟. 证明正交四球心间15个重心球及距离公式的算法[J]. 理论数学, 2019, 9(8): 880-889.







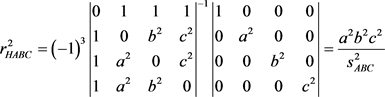
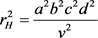 。
。
 球心2点直线参数方程为:
球心2点直线参数方程为: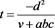 ,
;
;
;
;
。
,
;
;
;
;
。 ,坐标
)
,坐标
)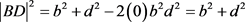 (垂心球距离公式)
(垂心球距离公式)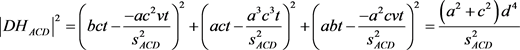 (2点坐标距离公式)
(2点坐标距离公式)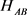 对
对
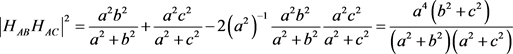 (垂心球距离公式)
(垂心球距离公式)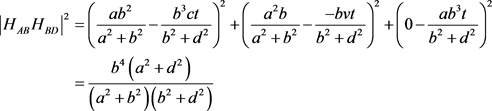 (2点坐标距离公式)
(2点坐标距离公式)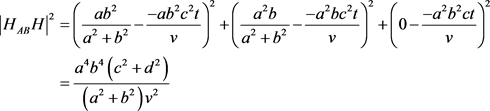 (2点坐标距离公式)
(2点坐标距离公式)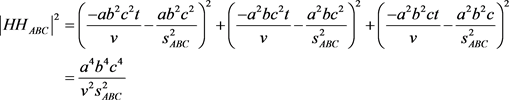 (2点坐标距离公式)
(2点坐标距离公式)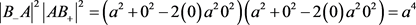
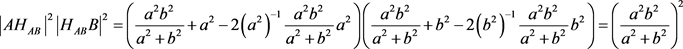
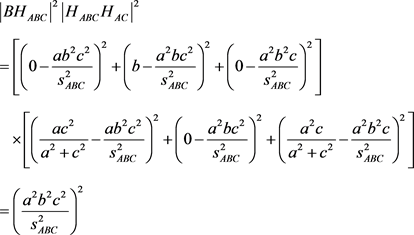
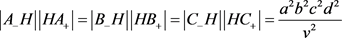 (略)
(略)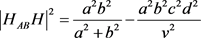 ;
;