Pure Mathematics
Vol.
11
No.
03
(
2021
), Article ID:
41393
,
10
pages
10.12677/PM.2021.113050
Littlewood-Paley积分与QK型空间的 刻画
崔洁
青岛大学数学与统计学院,山东 青岛
收稿日期:2021年2月18日;录用日期:2021年3月19日;发布日期:2021年3月31日

摘要
本文主要研究一类新的一维Q型空间——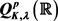 。首先给出了
。首先给出了 的若干基本性质。进而通过一类Littlewood-Paley函数
所构成的卷积算子,得到了该空间的Carleson测度刻画。
的若干基本性质。进而通过一类Littlewood-Paley函数
所构成的卷积算子,得到了该空间的Carleson测度刻画。
关键词
Q型空间,Carleson测度,Littlewood-Paley函数

Littlewood-Paley Integrals and the Characterization of QK Type Spaces
Jie Cui
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong
Received: Feb. 18th, 2021; accepted: Mar. 19th, 2021; published: Mar. 31st, 2021

ABSTRACT
In this paper, we introduce a new class of Q type spaces . We first investigate some basic properties of
. We first investigate some basic properties of . Further, via a family of convolution operators generated by Littlewood-Paley functions
, we establish a Carleson measure characterization of
. Further, via a family of convolution operators generated by Littlewood-Paley functions
, we establish a Carleson measure characterization of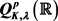 .
.
Keywords:Q-Type Space, Carleson Measure, Littlewood-Paley Function

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在调和分析和偏微分方程的研究中,Q型空间起到重要的作用。作为介于Sobolev空间和BMO空间之间的一类可微函数空间,Q型空间兼具两者的特点,一方面该空间具有平均振荡的性质,从而在调和分析研究中可以作为BMO空间的一个很好的替代。另一方面,该空间可以看作与Campanato-Sobolev型空间等价,因此在偏微分方程中具有很好的应用。在最近几十年中,Q型空间及其推广的形式得到了广泛的研究。最早Q型空间
是作为单位圆盘D上全纯BMO型空间
上的推广而提出的( [1] )。在2001年,Essen等人在文献 [2] 中将Q型空间推广到高维欧氏空间的情形,建立了
空间的实变理论,从而使Q型空间可以广泛应用到调和分析和偏微分方程的诸多课题的研究中,相关的研究进展参见文献 [3] [4] [5] [6]。
从几何的观点看,经典的Q型空间可以看作是一类与幂函数相关的加权函数空间,参见 [7]。当将幂函数替换为一个一般的权函数时,很自然地产生了相应的加权Q型空间。2002年,Essen,Xiao和Wulan在文献 [8] 中建立并研究了单位圆盘上与权函数相关的Q型空间
。
的高维实变形式由Bao和Wulan于2014年在文献 [9] 中引入,此后该类加权Q型空间得到了许多研究者的关注,参见文献 [10] [11] [12]。
本文在上述结果的基础上,引入一类新的Q型空间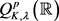 ,定义如下:
,定义如下:
定义1令
,设
是一个单调非减函数,则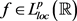 属于
属于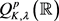 当且仅当
当且仅当

其中,I是
上的一个区间,
表示区间I的长度。
本文的主要目的是利用Carleson测度刻画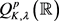 。BMO空间和经典的Q型空间的主要结果之一是这两类空间均可以通过Carleson测度进行刻画,参见 [2] [3]。在本文中,作者引入如下卷积算子:
。BMO空间和经典的Q型空间的主要结果之一是这两类空间均可以通过Carleson测度进行刻画,参见 [2] [3]。在本文中,作者引入如下卷积算子:
设f是
上的可测函数,并且满足:
(1)
假设
是
上的一个实值
函数且满足:
(2)
定义Littlewood-Paley积分:

首先,在第二节中,作者给出 的若干基本性质,并讨论了该空间与Campanato型空间
之间的关系。作为本文的主要结果,作者在第三节中利用上述定义的Littlewood-Paley积分
和与权函数相关的Carleson测度刻画
的若干基本性质,并讨论了该空间与Campanato型空间
之间的关系。作为本文的主要结果,作者在第三节中利用上述定义的Littlewood-Paley积分
和与权函数相关的Carleson测度刻画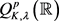 。
。
2.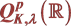 的基本性质
的基本性质
本节主要讨论 的一些基本性质。众所周知,经典的Q型空间
的一些基本性质。众所周知,经典的Q型空间 具有仿射不变性,即在平移,旋转和共形映射变换之下是不变的。由
具有仿射不变性,即在平移,旋转和共形映射变换之下是不变的。由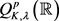 的定义,通过直接计算可以证明
的定义,通过直接计算可以证明 具有类似的性质。首先,我们可以得到
具有类似的性质。首先,我们可以得到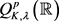 的一个简单刻画,即在共形映射和旋转下是保持不变的;其次,我们需要如下辅助函数:
的一个简单刻画,即在共形映射和旋转下是保持不变的;其次,我们需要如下辅助函数:
我们在本文中假设辅助函数
满足以下两个条件:
(3)
(4)
下面,我们证明 是非平凡的。
是非平凡的。
定义1 令
。若
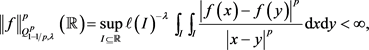
那么,称 ,其中I是
,其中I是 上的一个区间,
是区间I的长度。
上的一个区间,
是区间I的长度。
定理1 令
,有
,并且 是非平凡的。
是非平凡的。
证明 设I是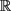 上的一个区间,对于任意
,有
,即
。因为K是一个非减的函数,所以
。对于任意
上的一个区间,对于任意
,有
,即
。因为K是一个非减的函数,所以
。对于任意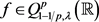 ,有
,有
故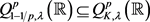 。而
。而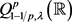 是非平凡的,故
是非平凡的,故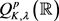 是非平凡的。
是非平凡的。
接下来,本文讨论新的 空间与经典函数空间的关系,首先我们引入Campanato型空间的定义:
空间与经典函数空间的关系,首先我们引入Campanato型空间的定义:
定义2 令
。若
,且满足
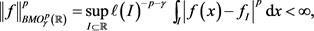
那么,称 。其中,
,I是
。其中,
,I是 上的一个区间,
表示区间I的长度。并且,该式中上确界取遍
上的一个区间,
表示区间I的长度。并且,该式中上确界取遍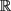 上所有长度为
的区间。
上所有长度为
的区间。
我们可以证明当
时,新的空间 是Campanato型空间
是Campanato型空间 的子空间。
的子空间。
定理2 是
的子空间,即
。
是
的子空间,即
。
证明 设 ,I是
,I是 上的一个区间,所以对任意
,如果
足够小,我们可以得到集合
,它的测度大于
。因为K是非减的,可得
上的一个区间,所以对任意
,如果
足够小,我们可以得到集合
,它的测度大于
。因为K是非减的,可得
注意到
,则对于一个足够小的
,可以得到
所以,
。从而完成了定理2的证明。
当权函数K进一步满足特定条件时,可以证明:
定理3 如果
,则有
。
证明 由定理2可知,
,所以只需证
。
注意到, 。而对于
。而对于 上的任意区间I和
上的任意区间I和 ,
,
,
所以,对任意 ,
,
因此, 。综上所述,
。综上所述, ,证明完成。
,证明完成。
3. 空间的Carleson型测度刻画
空间的Carleson型测度刻画
设I是 上任意区间,
上任意区间, 表示上半平面,定义如下Carleson方体:
表示上半平面,定义如下Carleson方体:

为简便起见,我们用
表示点 到其边界的距离,
类似;
到其边界的距离,
类似;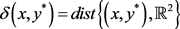 ,其中
为
,其中
为 关于坐标轴的对称点,即,如果
,那么
。
关于坐标轴的对称点,即,如果
,那么
。
下面引入
-Carleson测度的定义以及有关
- Carleson测度的刻画。
定义3 设
是 上的正Borel测度,则称
是一个
-Carleson测度,如果
上的正Borel测度,则称
是一个
-Carleson测度,如果
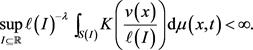
类似于经典Q型空间,可以证明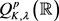 有类似的性质。
有类似的性质。
定理4 设
,并且K满足
,设
是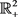 上的正Borel测度,则
是一个
- Carleson测度当且仅当
上的正Borel测度,则
是一个
- Carleson测度当且仅当 。
。
证明 必要性 若
是一个
-Carleson测度,设I是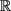 上的区间,并且以
为中心,长度为
。对任意正整数K,定义
为与I中心相同且边长为
的方体。再者,
指对应的Carleson方体。
上的区间,并且以
为中心,长度为
。对任意正整数K,定义
为与I中心相同且边长为
的方体。再者,
指对应的Carleson方体。
从而,易知
进而,
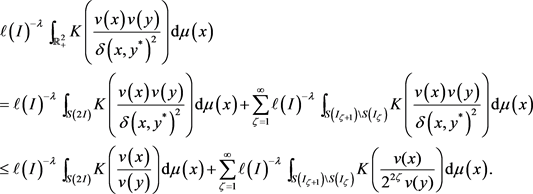
由假设知,
是一个
-Carleson测度,
。
综上所述,可以推出

充分性 下面,记Carleson方体
的中心为y,那么可知,现在
。如果
,
就有
,因此可以得到,
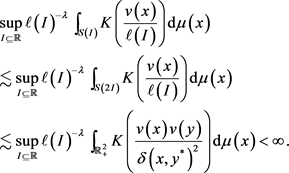 (5)
(5)
此时,如果(5)式成立,则
是一个
-Carleson测度。从而定理4得证。
为了进一步研究 的Carleson测度刻画,给出如下两个引理:
的Carleson测度刻画,给出如下两个引理:
引理1 设
,若K满足(3),则
。
引理2 令
。设非负函数
和h在
上可测,对于所有可测函数
,可得到以下Hardy型不等式:
(i)
成立,当且仅当
(ii)
成立,当且仅当
其中C的取值依赖于p,A或者B。
借助于上面给出的引理1和引理2,接下来利用Liitlewood函数
的性质给出本文的主要结果:
定理5 设 并且满足(1)式,其中
。假设K满足(3),(4),那么
并且满足(1)式,其中
。假设K满足(3),(4),那么
(i) 如果 ,则
是一个
-Carleson测度;
,则
是一个
-Carleson测度;
(ii) 如果
,则若
是一个
-Carleson测度,有 。
。
证明 (i) 设I和J都是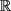 上以
为中点的区间,并且有
。不失一般性,我们假设
。
上以
为中点的区间,并且有
。不失一般性,我们假设
。
设函数
满足
则有
。
对f作分解,
,其中
根据引言中Littlewood-Paley函数
的定义以及限制条件(2),易知
从而,
又由Minkowski不等式,可得
这里
,上述计算中的最后一步使用了球坐标变换。设
从而有
因此,
其中,
对于
,注意到
根据引理1,易得
因此,由Hölder不等式以及球坐标变换,可得
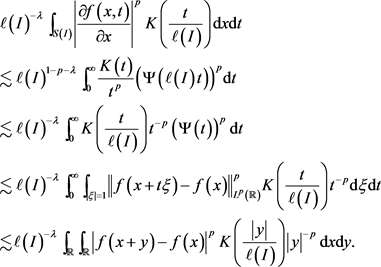
注意到,
可得
。
同理可得,
。
因此,
,其中,
类似于上面的过程,继续将其分解讨论,如此进行下去,最终可得
(ii) 由三角不等式,易知
 ,
,
其中,
对于
,根据Minkowski不等式易知
所以,由引理1和引理2我们可以得到
同理,
。
对于
,易知
。
因此, 。这就完成了定理5的证明。
。这就完成了定理5的证明。
致谢
作者衷心感谢李澎涛教授的指导与建议。
基金项目
山东省自然科学基金(项目编号:ZR2020MA004);国家自然科学基金(项目编号:11471176)。
文章引用
崔 洁. Littlewood-Paley积分与QK型空间的刻画
Littlewood-Paley Integrals and the Characterization of QK Type Spaces[J]. 理论数学, 2021, 11(03): 377-386. https://doi.org/10.12677/PM.2021.113050
参考文献
- 1. Aulaskari, R., Xiao, J. and Zhao, R. (1995) On Subspaces and Subsets of BMOA and UBC. Analysis, 15, 101-121.
https://doi.org/10.1524/anly.1995.15.2.101
- 2. Essén, M., Janson, S., Peng, L. and Xiao, J. (2000) Q Spaces of Several Real Variables. Indiana University Mathematics Journal, 49, 575-615. https://doi.org/10.1512/iumj.2000.49.1732
- 3. Dafni, G. and Xiao, J. (2004) Some New Tent Spaces and Duality Theorems for Fractional Carleson Measures and . Journal of Functional Analysis, 208, 377-422. https://doi.org/10.1016/S0022-1236(03)00181-2
- 4. Wu, Z. and Xie, C. (2003) Q Spaces and Morrey Spaces. Journal of Functional Analysis, 201, 282-297.
https://doi.org/10.1016/S0022-1236(03)00020-X
- 5. Xiao, J. (2007) Homothetic Variant of Fractional Sobolev Space with Application to Navier-Stokes System. Dynamics of Partial Differential Equations, 4, 227-245. https://doi.org/10.4310/DPDE.2007.v4.n3.a2
- 6. Li, P. and Zhai, Z. (2010) Well-Posedness and Regularity of Generalized Navier-Stokes Equations in Some Critical Q-Spaces. Journal of Functional Analysis, 259, 2457-2519. https://doi.org/10.1016/j.jfa.2010.07.013
- 7. Essén, M. and Wulan, H. (2002) On Analytic and Meromorphic Function and Spaces of Q_K-Type. Illinois Journal of Mathematics, 46, 1233-1258.
- 8. Essén, M., Wulan, H. and Xiao, J. (2006) Several Function-Theoretic Characterizations of Möius Invariant Spaces. Journal of Functional Analysis, 230, 78-115. https://doi.org/10.1016/j.jfa.2005.07.004
- 9. Bao, G. and Wulan, H. (2014) Spaces of Several Real Variables. Abstract and Applied Analysis, 2014, 1-14.
https://doi.org/10.1155/2014/931937
- 10. 陈萱. 与权函数相关的一维实变Q型空间的Carleson型刻画[J]. 理论数学, 2020, 10(10): 990-995.https://doi.org/10.12677/PM.2020.1010116
- 11. Han, F. and Li, P. (2020) Characterizations for a Class of Q-Type Spaces of Several Real Variables. Advances in Mathematics (China), 49, 195-214.
- 12. Wulan, H. and Zhou, J. (2014) Decom-position Theorems for Spaces and Applications. Forum Mathematicum, 26, 467-495. https://doi.org/10.1515/form.2011.174

 。首先给出了
。首先给出了 的若干基本性质。进而通过一类Littlewood-Paley函数
所构成的卷积算子,得到了该空间的Carleson测度刻画。
的若干基本性质。进而通过一类Littlewood-Paley函数
所构成的卷积算子,得到了该空间的Carleson测度刻画。

 . We first investigate some basic properties of
. We first investigate some basic properties of . Further, via a family of convolution operators generated by Littlewood-Paley functions
, we establish a Carleson measure characterization of
. Further, via a family of convolution operators generated by Littlewood-Paley functions
, we establish a Carleson measure characterization of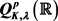 .
.


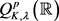 ,定义如下:
,定义如下: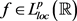 属于
属于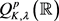 当且仅当
当且仅当
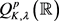 。BMO空间和经典的Q型空间的主要结果之一是这两类空间均可以通过Carleson测度进行刻画,参见 [2] [3]。在本文中,作者引入如下卷积算子:
。BMO空间和经典的Q型空间的主要结果之一是这两类空间均可以通过Carleson测度进行刻画,参见 [2] [3]。在本文中,作者引入如下卷积算子:
 的若干基本性质,并讨论了该空间与Campanato型空间
之间的关系。作为本文的主要结果,作者在第三节中利用上述定义的Littlewood-Paley积分
和与权函数相关的Carleson测度刻画
的若干基本性质,并讨论了该空间与Campanato型空间
之间的关系。作为本文的主要结果,作者在第三节中利用上述定义的Littlewood-Paley积分
和与权函数相关的Carleson测度刻画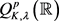 。
。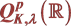 的基本性质
的基本性质 的一些基本性质。众所周知,经典的Q型空间
的一些基本性质。众所周知,经典的Q型空间 具有仿射不变性,即在平移,旋转和共形映射变换之下是不变的。由
具有仿射不变性,即在平移,旋转和共形映射变换之下是不变的。由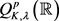 的定义,通过直接计算可以证明
的定义,通过直接计算可以证明 具有类似的性质。首先,我们可以得到
具有类似的性质。首先,我们可以得到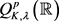 的一个简单刻画,即在共形映射和旋转下是保持不变的;其次,我们需要如下辅助函数:
的一个简单刻画,即在共形映射和旋转下是保持不变的;其次,我们需要如下辅助函数: 是非平凡的。
是非平凡的。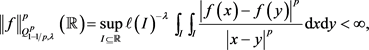
 ,其中I是
,其中I是 上的一个区间,
是区间I的长度。
上的一个区间,
是区间I的长度。 是非平凡的。
是非平凡的。 上的一个区间,对于任意
,有
,即
。因为K是一个非减的函数,所以
。对于任意
上的一个区间,对于任意
,有
,即
。因为K是一个非减的函数,所以
。对于任意 ,有
,有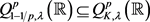 。而
。而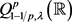 是非平凡的,故
是非平凡的,故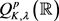 是非平凡的。
是非平凡的。 空间与经典函数空间的关系,首先我们引入Campanato型空间的定义:
空间与经典函数空间的关系,首先我们引入Campanato型空间的定义: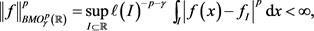
 。其中,
,I是
。其中,
,I是 上的一个区间,
表示区间I的长度。并且,该式中上确界取遍
上的一个区间,
表示区间I的长度。并且,该式中上确界取遍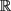 上所有长度为
的区间。
上所有长度为
的区间。 是Campanato型空间
是Campanato型空间 的子空间。
的子空间。 是
的子空间,即
。
是
的子空间,即
。 ,I是
,I是 上的一个区间,所以对任意
,如果
足够小,我们可以得到集合
,它的测度大于
。因为K是非减的,可得
上的一个区间,所以对任意
,如果
足够小,我们可以得到集合
,它的测度大于
。因为K是非减的,可得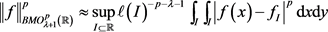 。而对于
。而对于 上的任意区间I和
上的任意区间I和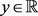 ,
, ,
, 。综上所述,
。综上所述,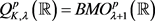 ,证明完成。
,证明完成。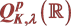 空间的Carleson型测度刻画
空间的Carleson型测度刻画 上任意区间,
上任意区间, 表示上半平面,定义如下Carleson方体:
表示上半平面,定义如下Carleson方体:
 到其边界的距离,
类似;
到其边界的距离,
类似;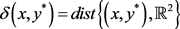 ,其中
为
,其中
为 关于坐标轴的对称点,即,如果
,那么
。
关于坐标轴的对称点,即,如果
,那么
。 上的正Borel测度,则称
是一个
-Carleson测度,如果
上的正Borel测度,则称
是一个
-Carleson测度,如果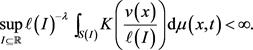
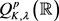 有类似的性质。
有类似的性质。 上的正Borel测度,则
是一个
- Carleson测度当且仅当
上的正Borel测度,则
是一个
- Carleson测度当且仅当 。
。 上的区间,并且以
为中心,长度为
。对任意正整数K,定义
为与I中心相同且边长为
的方体。再者,
指对应的Carleson方体。
上的区间,并且以
为中心,长度为
。对任意正整数K,定义
为与I中心相同且边长为
的方体。再者,
指对应的Carleson方体。

 (5)
(5) 的Carleson测度刻画,给出如下两个引理:
的Carleson测度刻画,给出如下两个引理: 并且满足(1)式,其中
。假设K满足(3),(4),那么
并且满足(1)式,其中
。假设K满足(3),(4),那么 ,则
是一个
-Carleson测度;
,则
是一个
-Carleson测度; 。
。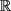 上以
为中点的区间,并且有
。不失一般性,我们假设
。
上以
为中点的区间,并且有
。不失一般性,我们假设
。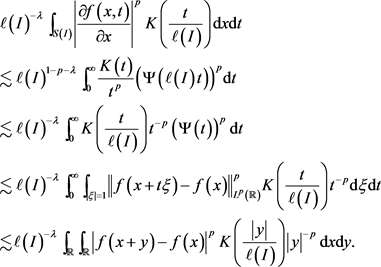
 ,
, 。这就完成了定理5的证明。
。这就完成了定理5的证明。