ABSTRACT

The existing methods for extracting the translation and scale invariants from the discrete orthogonal moments are via a linear combination of the corresponding invariants of geometric moments or image normalization, which led to calculational errors. In this paper, a novel kind of discrete orthogonal moments named as Charlier moment is proposed based on the discrete Charlier polynomials, and then an approach to directly derive the translation and scale invariants from Charlier moments is also presented. Experimental results show the high classification and representation accuracy of these invariants as a result of direct calculation instead of the image normalization or a linear combination of the corresponding invariants of geometric moments. It is also shown that these invariants are relatively robust in the presence of image noise and are potentially useful as a kind of invariant descriptors in some image analysis and pattern recognition.

Keywords:Discrete Orthogonal Moments, Charlier Polynomials, Translation, Scale Invariants, Pattern Recognition

基于Charlier矩的图像分析

时光慧，王晅

陕西师范大学物理学与信息技术学院，陕西 西安

收稿日期：2017年4月10日；录用日期：2017年4月23日；发布日期：2017年4月27日

摘 要

针对离散正交矩的平移和尺度不变量只能通过图像归一化或者借助几何矩不变量的线性组合间接获取，会带来较大的表示误差，本文基于离散Charlier多项式，提出了一种新的离散正交矩——Charlier矩，并给出了Charlier矩平移与尺度不变量的直接计算方法。实验表明，由Charlier矩直接计算的平移和尺度不变量与现有方法相比，具有较高的表示精度与分类准确率，而且对图像噪声有较强的稳定性，可以应用于图像不变分析与目标识别等应用领域。

关键词 :离散正交矩，Charlier多项式，平移和尺度不变量，模式识别

Copyright © 2017 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

1962年Hu [1] 提出的图像几何矩理论受到广泛关注。图像几何矩不变描述量具有平移、旋转和尺度不变的特性，而且计算效率较高，可以应用于图像不变分析与机器视觉的各个领域。然而，几何矩的基函数是非正交的，导致了较大的信息冗余，所以基于几何矩重构图像是非常困难的，而且该类矩对图像噪声非常敏感，带来一定的表示误差与分类错误率。针对以上问题，一些研究工作者基于连续正交基函数提出了Zernike [2] [3] [4] 和Legendre [5] 等连续正交矩。由于连续正交矩的基函数是正交的连续函数，所以可以具有较小的信息冗余，基于连续正交矩可以对图像精确重构，此外，与几何矩相比，对噪声有更好的稳定性。但是，由于连续正交矩的定义涉及到二维连续积分形式，而数字图像是定义在离散域的数字矩阵，所以计算过程中需要进行坐标转换和积分近似，所以存在数值积分近似误差与几何误差 [4] 。这些误差会严重影响图像的重构精度与分类精度。

Mukundan [6] 在2001年提出一种基于离散Tchebichef多项式的离散正交矩。随后，Yap [7] 提出另一种基于Krawtchouk多项式的离散正交矩。离散正交矩的基函数与数字图像域完全匹配，定义与计算过程消除了由坐标转换和近似误差引起的数值积分近似误差与几何误差，具有良好的图像表征能力与分类精度，而且与连续正交矩相比，抵抗噪声的干扰能力也明显增强，然而，离散正交矩缺乏本质上的平移与尺度变换不变性，平移和尺度不变量是通过图像平移与尺度归一化方法或者借助几何矩不变量的线性组合间接获取通，这一过程会引入新的计算误差，从而影响离散正交矩的优良性能。本文基于Charlier离散正交多项式 [8] ，提出了一种新的离散正交矩，并基于该离散正交多项式的特殊性质，提出一种直接计算该矩的平移和尺度不变量的方法。实验结果验证了该方法所获得的Charlier离散正交矩尺度和平移不变量具有很好的表示与分类性能。

2. Charlier离散正交矩

大小为的图像函数为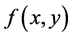，二维Charlier矩 [8] 定义如下：

(1)

其中，和分别表示n阶和m阶标准Charlier离散正交多项式。n阶Charlier多项式可用超几何函数定义如下：

(2)

其中，

(3)

(4)

有

(5)

因此，n阶Charlier 多项式可以写为：

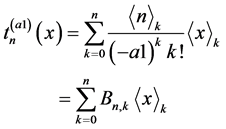(6)

其中，

(7)

(8)

其中，表示第一类斯特林数，有以下递归关系：

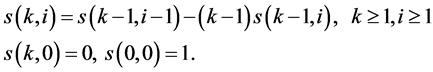(9)

离散Charlier多项式和，，，满足以下正交关系：

(10)

其中，表示平方模，表示狄拉克函数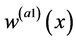，是加权函数，有

(11)

(12)

由此，n阶标准Charlier离散正交多项式为：

(13)

根据公式(6)，(7)，(8)和(13)，又可以写成：

(14)

可以证明，标准Charlier离散正交多项式存在以下递推关系，

(15)

其中，

(16)

零阶和一阶Charlier多项式为：

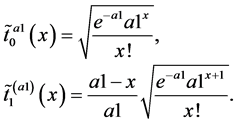(17)

根据以上的递推关系，可以实现Charlier基函数的快速计算，从而提高Charlier矩的计算速度。

3. Charlier矩不变量的快速计算

3.1. Charlier矩的平移不变量

给定图像，为了计算其平移与尺度变换不变量，进行以下的预处理，

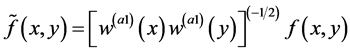(18)

计算预处理后的图像对应用的质心坐标，有

(19)

对应的Charlier中心矩为

(20)

表示归一化后的Charlier多项式：

(21)

运用式子(8)和(14)，又可写为：

(22)

其中有，

(23)

平移Charlier多项式可以表示为下面可分离形式：

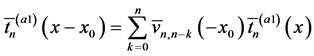(24)

有

(25)

类似地，y轴方向上的平移Charlier多项式可以写成：

(26)

和

(27)

公式(20)表示的Charlier中心距又可以写成：

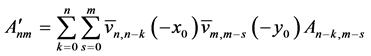(28)

由上可知，Charlier中心距可以用Charlier矩线性表示。根据上述的递推关系，Charlier矩的平移不变量可以快速的计算出来。

3.2. 尺度不变量

假设原始图像在横轴和纵轴上的尺度因子分别为a和b，则预处理后的图像函数尺度化后的Charlier矩为：

(30)

由公式(10)和(23)，我们可以把归一化的多项式写成：

(31)

其中，

(32)

因此，横轴方向的尺度化Charlier多项式可以表示为：

(33)

未经过尺度化的多项式和尺度化后的多项式之间的数学关系为：

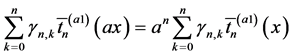， (34)

其中，

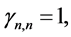
(35)

类似的，纵轴方向的Charlier多项式可以表示为：

(36)

因此，有如下：

(37)

通过消除因子a和b，我们可以推导出Charlier矩的尺度不变量：

(38)

根据(32)、(33)、(35)表示的递推公式，我们可以快速计算出来尺度不变量。由上式可知，尺度不变量来也可以表示平移不变量，即尺度不变量也可以表示为尺度平移不变量。

4. 仿真实验

为了验证本文方法的性能，选择大小为英文字母、汉字“幕”二值图像与“招财猫”及蝴蝶灰度图像进行了实验仿真，并于最新的图像平移与尺度不变量计算方法-Tchebichef不变量 [9] 进行了性能比较。仿真实验的主要目的是首先测试本文方法计算的平移不变量与尺度不变量的稳定性，其次测试基于上述不变量的分类性能及对图像噪声干扰的鲁棒性。

4.1. 平移不变量的稳定性

实验采用大小为的汉字“幕”和的英文字符“Z”，在x与y方向进行了平移量为−2到2，增量为1的平移操作，通过本文方法计算平移不变量，相应结果见表1和表2，可以看出，由本文方法计算的平移不变量具有很好的稳定性。

4.2. 尺度不变量

实验采用大小为灰度图像“招财猫”，分别进行了尺度因子为0.6到1.4，增量为0.2的尺度变换，对变换结果利用本文方法计算尺度变换不变量与文献 [9] 方法计算Tchebichef不变量，相应结果见表3和表4，可以看出，由本文方法计算的尺度变换平移不变量具有很好的稳定性，而文献 [9] 方法计算的Tchebichef不变量变化范围较大，说明本文方法具有更好的计算精度与不变表示能力。

表 1. 英文字符“Z”部分Charlier中心矩

表 2. 汉字“幕”部分Charlier中心矩

表 3. 招财猫 Charlier矩尺度不变量

表 4. 招财猫 Tchebichef矩尺度不变量

4.3. 分类性能

实验采用大小为的26个英文字符二值图像数据集与蝴蝶灰度图像数据集，进行了平移与尺度变换不变分类，选用以下的6个不变量作为分类特征，

(39)

选择欧氏距离作为衡量特征向量的相似性度量，欧氏距离定义为

(40)

其中是未知样本的T维特征向量，是k类的训练向量，选取最近邻分类方法进行分类，性能测评指标采用分类正确率，定义如下

(41)

实验1：采用26个大写字母图像作为训练集，对于训练集中的每幅图像进行平移变换和尺度变换，尺度因子，平移量为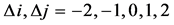，并对每幅变换后的图像感染密度为0%~4%，增量为1%的椒盐噪声得到测试集，测试集中的部分图像见图1，应用本文方法计算出的Charlier(C)与文献 [9] 方法计算的Tchebichef(T)不变量进行分类，分类结果见表5。可以看出，在未感染噪声的情况下，本文方法可以对所有全部测试图像进行正确分类，而文献 [9] 的方法正确分类率仅有37%。随着噪声感染的密度增加，正确识别率也明显降低，但均显著高于文献 [9] 的方法，说明本文方法在噪声干扰的情况下，也能获得一定的识别精度。

实验2：采用七张蝴蝶灰度图片作为训练集，对于训练集中的每幅图像进行平移变换和尺度变换，尺度因子,平移量为，并对每幅变换后的图像感染密度为0%~4%，增量为1%的椒盐噪声得到测试集，测试集中的部分图像见图2，应用本文方法计算出的Charlier(C)与文献 [9] 方法计算的Tchebichef(T)不变量进行分类，分类结果见表6。可以看出，对于灰度图像，在未感染噪声的情况下，本文方法正确识别率显著高于文献 [9] 的方法。对噪声干扰的鲁棒性也明显好于文献 [9] 的方法。

图1. 实验一部分测试集

图2. 实验二部分测试集

表5. 大写字母的分类结果

表6. 蝴蝶图片的分类结果

5. 结论

本文基于Charlier多项式提出了一种新的离散正交矩——Charlier矩，并给出了Charlier矩平移与尺度不变量的直接计算方法。与现有离散矩的平移与尺度不变量的计算方法相比，具有更好的计算精度。实验验证了本文方法较现有最新方法在二值图像与灰度图像都具有非常好的稳定性与分类精度，并对噪声干扰也具有较高的鲁棒性，作为平移与尺度不变特征描述可以应用于数字图像分析与机器视觉的相关领域。

文章引用

时光慧,王 晅. 基于Charlier矩的图像分析
Image Analysis by Charlier Moments[J]. 计算机科学与应用, 2017, 07(04): 359-368. http://dx.doi.org/10.12677/CSA.2017.74044

参考文献 (References)