Computer Science and Application
Vol.08 No.04(2018), Article ID:24530,7
pages
10.12677/CSA.2018.84055
A Discovery of New Template Design of CT System Model
Xuanlin Chen1, Tao Luo1, Huiling He1, Fang Wang1,2*
1College of Science, Hunan Agricultural University, Changsha Hunan
2Agricultural Mathematical Model and Data Process Center, Hunan Agricultural University, Changsha Hunan

Received: Apr. 4th, 2018; accepted: Apr. 19th, 2018; published: Apr. 26th, 2018

ABSTRACT
Computed Tomography (CT) technology has been widely used in the field of medicine and engineering. The shape of the template is crucial to the calibration of CT system parameters. In this paper, the ordinary single ellipse and small circle template are improved. We design three new templates. The receiving information is obtained by Radon transform and R-L filter firstly, and then their reconstruction images are acquired based on convolution back projection reconstruction algorithm. Furthermore, we make a quantitative assessment of the reconstruction effect by the sensitivity, specificity and Youden index. In addition, in order to investigate the anti-noise, the original template and the new templates are added to the Gauss noise of different strength, respectively. The experimental result shows that the new templates have better noise resistance than the original template. An interesting finding is that the template generated by geometric figure of a single reference frame with polygon outline is better than the template produced by multi reference frame geometry with the arc line for the reconstruction of CT.
Keywords:Polygon Template, Computed Tomography (CT), Convolution, R-L Filtering, Youden Index
CT系统模型新模板设计的发现
陈宣霖1,罗涛1,何慧玲1,王访1,2*
1湖南农业大学理学院,湖南 长沙
2湖南农业大学农业数学建模与数据处理中心,湖南 长沙

收稿日期:2018年4月4日;录用日期:2018年4月19日;发布日期:2018年4月26日

摘 要
计算机断层扫描(Computed Tomography, CT)技术被广泛地应用于医学、工程领域。模板的形状对CT系统参数标定至关重要,本文针对普通的单椭圆和小圆模板进行了改进,设计了三种新的模板。首先利用Radon变换和R-L滤波获取其接收信息,然后基于卷积反投影重建算法得到其重建图,并利用敏感度、特异度和约登指数对重建效果进行了定量评估。与原模板相比,新模板重建效果更好。此外,为了考察其抗噪性,对原模板和新模板分别加入不同强度的高斯噪声,试验结果表明新模板比原模板具有更好的抗噪性。一个有趣的发现是以多边形轮廓的单参考系几何图形比边缘为弧线的多参考系几何图形为模板对CT重建效果更好。
关键词 :多边形模板,CT,卷积,R-L滤波,约登指数

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在临床医学上,计算机断层扫描(CT)技术是应用非常广泛的影像技术,该技术以多个X射线的投影来获得穿过人体内部的X射线密度值,由此形成人体某个组织的断层切片图像,并通过三维重建得到人体内部器官和组织的立体图像 [1] 。X射线处理同时配接X光机可以实现动态显示人体内的器官与组织的细节部分。而CT中的模板可以迅速确定其旋转中心的位置,以及可以衡量图像还原的好坏程度,因此模板的设计选择对于CT技术的效果至关重要。在CT图像还原方面,Sidky等推导出了BPF重建算法,该算法可用于直线CT图像重建 [2] 。Katsevich提出了螺旋轨迹的滤波反投影重建算法。先对投影数据沿着指定方向进行一维Hilbert变换,然后通过反投影得到重建图像 [3] 。郭威 [4] 改进的ART算法提高了收敛速度,使原图像还原度更高。莫华等 [5] 利用卷积反投影重建算法对CT图像进行重构。Wang等 [6] 利用约登指数衡量图像还原程度的好坏。
针对之前的研究成果,基于平行射束的模板设计,本文提出了几种新型模板,选取使用卷积反投影算法对图像进行重构后,用约登指数进行检验图质的还原程度,同时对模板进行加噪处理,对比得到还原程度最好的模板,且抗噪性能最佳的模板。该模板可应用于实际CT图像系统的参数标定,有利于更加准确的标定CT系统的参数。
2. 数据来源和模型假设
本研究对象来源于2017年全国大学生数学建模竞赛数据,如图1所示。为了简化,作以下假设:1)数据来源中的两个几何图形为椭圆和小圆;2) CT系统旋转中心在探测器组的中垂线上;3) 不考虑X射线的在介质表面反射造成的影响;4) 探测器接收到的射线能量经过的增益为等倍数增益;5) 不考虑由于CT系统旋转而产生的X射线散射效应。
3. 卷积反投影重构图像
在进行卷积反投影重建时,由于噪声对CT扫描工作的影响,因此有必要对其进行滤波处理。下面我们利用原始数据与滤波函数的卷积运算,得到各方向卷积的投影函数,以期获取信噪比更高的图像。采用R-L滤波器 [7] ,其函数如下,
(1)
其中d为采样间隔,记
为原始投影函数, 为滤波之后的投影函数,则:
为滤波之后的投影函数,则:
(2)
之后将滤波之后的投影函数 进行射束计算与内插。由于数据为离散数据,可能存在间距过大时数据缺失,所以进行内插对数据进行插补,而射束计算的目的是计算出内插公式中的 和权重δ。内插公式如下:
(3)
对于任意的像素 ,以及旋转角度θ有:
(4)
令 ,则射束运算如下:
(5)
经过射束计算与内插后,利用累加反投影法得到任意一点 的图像。进行初始化,定义所有像素 ,令 ,Δ为角增量, 。
(6)
根据以下递推公式进行计算:
(7)
当 时,图像重建完毕。卷积反投影重建流程图 [8] 如下。
4. 基于不同滤波器下新模板的构建与对比
新模板下的图像重建
由于椭圆和小圆的边界圆润,在提取其接收信息二值图边缘时可能产生的边缘信息冗余或不连续现象 [9] ,这样计算得到标定信息可能存在误差。我们重新设计了三种新的模板,大小仍为256像素 * 256像素,其吸收率灰度图像记为 ,如图2第1列所示。
记吸收率为1的区域为 (有介质的区域),吸收率为0的区域为 (没有介质的区域),则有 ,且 。为了考察新模板接收信息的重建图像的效果,并与原模板(图1)进行比较。为简单起见,我们设定CT系统的旋转中心为模板几何中心 [10] ,以1˚

Figure 1. Template map of the original data
图1. 原始数据模板图
的步长从1˚旋转到360˚,利用Radon变换 [11] 获取其接收信息,如图2第2列所示。利用上述提出的基于卷积反投影函数重建的方法对图2第2列图像重建,得到重建图
,如图2第3列所示,重建效果图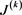 基本与原图
吻合,效果较好。
基本与原图
吻合,效果较好。
为了进一步定量比较新模板与原模板的优劣,借用医学评价筛查试验真实性的方法,重新定义敏感度(sensitivity,Se)和特异度(specificity,Sp)。敏感度定义为有介质的区域重建正确率,特异度定义为没有介质的区域重建正确率 [12] 。并利用约登指数 [13] (Youden指数 = Se + Sp − 1)综合评价敏感度与特异度。上述三个指标的计算如(15)式所示。原模板与新模板 重建后的Se、Sp和Youden指数如表1所示:结果表明新模板下得到的敏感度和特异度均优于原模板,以新模板 的效果最优。
(8)
其中,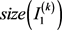 表示新模板
表示新模板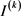 中有介质区域的像素点总个数,
表示新模板
中没有介质区域的像素点总个数。
中有介质区域的像素点总个数,
表示新模板
中没有介质区域的像素点总个数。
更进一步,由于实际工作中CT系统对对象进行断层扫描时,容易受到噪声影响 [14] ,因此,对新模板 与原模板分别加入5组不同强度的高斯噪声 [15] ,并利用Radon变换获取它们的接收信息,最后利用3节中提出的基于卷积反投影函数重建的算法得到重建图像,并利用Youden指数定量评价其效果,为消除随机因素的影响,对每次加噪过程重复100次,得到的平均结果如表2所示。原模板和新模板的重建效果如图3所示,Youden指数改变率随噪声强度的变化情况如图4所示。
从表2及图4、图5可以看出,随着噪声强度的增加,原模板和三个新模板的敏感度和特异度均有下降趋势,但新模板的重建效果总是优于原模板。表明设计的新模板在抗噪性方面优于原模板。然而,新模板2和新模板3的Youden指数变化率显著小于原模板和新模板1,这个现象表明以多边形轮廓的几
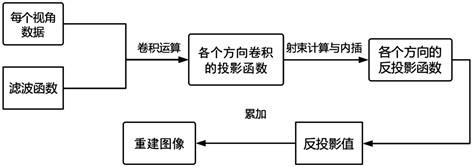
Figure 2. Reconstruction flow chart based on convolution back projection
图2. 基于卷积反投影重建流程图
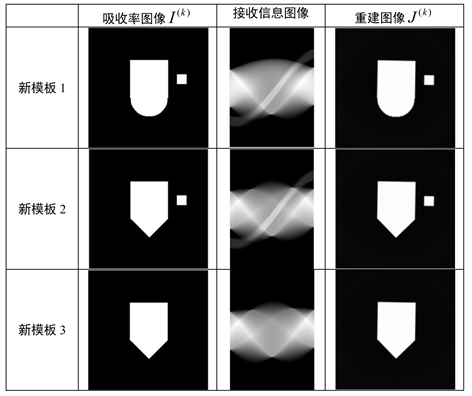
Figure 3. Reception information and reconstruction effect of new templates. The first column is absorptivity matrix gray image; the second column is receiving information gray image; and the third column is the reconstructed image
图3. 新模板的接收信息与重建效果。第1列为吸收率矩阵灰度图;第2列为接收信息灰度图;第3列为重建图像
Table 1. Reconstruction effect of original template and three new templates
表1. 原模板与新模板 重建效果
何图形比边缘为弧线的几何图形为模板对于CT重建效果更好。
5. 结语
参照将边缘弧线变为边缘为多边形,且参考系逐步减少的原则设计了三个新模板。本文对初始模板和新设计的三个模板采用Radon变换得到接收图像的信息,然后对接收图像信息进行R-L滤波,采用平
Table 2. Youden index of reconstruction effect of original template and new templates under different noise intensity
表2. 在不同强度噪声下原模板与三个新模板重建效果的Youden指数

Figure 4. Reconstruction effect diagram of original template and new templates under different noise intensity
图4. 原模板和新模板在不同噪声强度下的重建效果图
行射束卷积反投影算法得到还原的模板图像及衡量图像还原质量的约登指数发现以多边形轮廓的几何图形比边缘为弧线的几何图形为模板对CT重建效果更好。由于上述还原条件为理想状态,因此为了适应现实中含有各种对图像质量影响的条件,对所有的模板进行逐步加高斯噪声,并计算每个加噪模板还原后的约登指数,通过对比发现,新模板2和新模板3的Youden指数变化率显著小于原模板和新模板1,研究结果为:以多边形轮廓的单参考系几何图形比边缘为弧线的多参考系几何图形为模板的重建效果更优。

Figure 5. The change rate of Youden index of original template and the three new templates with increasing noise intensity
图5. 原模板与三个新模板的Youden指数变化率随噪声强度的变化
因此,在CT系统模板设计时,可以参考以多边形轮廓的单参考系几何图形,这有利于CT系统的参数标定的准确性。
基金项目
本文由湖南农业大学大学生科创项目(XCX16005)资助。
文章引用
陈宣霖,罗 涛,何慧玲,王 访. CT系统模型新模板设计的发现
A Discovery of New Template Design of CT System Model[J]. 计算机科学与应用, 2018, 08(04): 496-502. https://doi.org/10.12677/CSA.2018.84055
参考文献
- 1. 李想. CT图像的应用研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2004.
- 2. Sidky, E.Y., Zou, Y. and Pan, X. (2005) Volume Image Reconstruction from a Straight-Line Source Trajectory. Nuclear Science Symposium Conference Record, Fajardo, 23-29 October 2005, 2441-2444.
- 3. Katsevich, A. (2002) Theoretically Exact Filtered Backprojection-Type Inversion Algorithm for Spiral CT. Siam Journal on Applied Mathematics, 62, 2012-2026. https://doi.org/10.1137/S0036139901387186
- 4. 郭威. CT不完全投影数据重建算法研究[D]: [博士学位论文]. 长春: 吉林大学, 2011.
- 5. 莫华, 龙莉玲. X-CT图像重建的卷积反投影图解法[J]. 中国医学物理学杂志, 1999, 16(3): 143-145.
- 6. Wang, F., Wang, L. and Zou, R.B. (2014) Multifractal Detrended Moving Average Analysis for Texture Representation. Chaos: An Interdisciplinary Journal of Nonlinear Science, 24, Article ID: 033127.
- 7. 王晓鹏, 王明泉, 侯慧玲. 基于R-L-MS-L滤波函数的CT图像重建[J]. 电视技术, 2014, 38(7): 26-28.
- 8. 庄天戈. CT原理与算法[M]. 上海: 上海交通大学出版社, 1992.
- 9. 刘云云. 基于纹理子空间成分的活动轮廓模型的图像分割[D]: [硕士学位论文]. 大连: 大连理工大学, 2009.
- 10. 李保磊, 张耀军. 基于对称投影的2D-CT系统投影旋转中心自动确定方法[C]//全国射线数字成像与CT新技术研讨会论文集. 上海.
- 11. 王金平. 平面Radon变换的反演公式[J]. CT理论与应用研究, 2000, 9(1): 8-11.
- 12. 杨志伟, 傅炳南. 发热出疹性疾病的临床诊断及其特异度和敏感度的分析[J]. 中国疫苗和免疫, 1999(2): 76-79.
- 13. 李雪迎. 诊断能力评价的统计学方法——准确度与约登指数[J]. 中国介入心脏病学杂志, 2011, 19(4): 213-213.
- 14. 赵勇, 李品江. CT噪声和伪影对成像质量的影响及控制[J]. 中华放射学杂志, 1997(1): 56-58.
- 15. 王卫江. 实时高斯噪声产生方法[J]. 仪器仪表学报, 2006, 27(11): 1523-1525.
NOTES
*通讯作者。
