Advances in Social Sciences
Vol.
08
No.
11
(
2019
), Article ID:
32996
,
9
pages
10.12677/ASS.2019.811257
Analysis and Prediction of 92# Gasoline Price in Beijing Based on Residual Autoregressive Model
Xiaogang Li
Yunnan University of Finance and Economics, Kunming Yunnan

Received: Oct. 28th, 2019; accepted: Nov. 11th, 2019; published: Nov. 18th, 2019

ABSTRACT
Oil price is related to the national economy and people’s livelihood. This paper selects the price data of 92# gasoline for price adjustment date from January 2013 to November 2018 in Beijing. The residual autoregression model is used to investigate its fluctuation trend, extract its internal change rule and make prediction, which can provide reference for the government to adjust and control price, enterprises to make production decisions and people to maintain normal life and production order.
Keywords:Gasoline Price, Residual Autoregressive Model, ARCH Model
基于残差自回归模型的北京市92#汽油价格的 分析与预测
李小刚
云南财经大学,云南 昆明

收稿日期:2019年10月28日;录用日期:2019年11月11日;发布日期:2019年11月18日

摘 要
油价关系国计民生。本文选取北京市2013年1月至2018年10月的92#汽油调整日的价格数据,运用残差自回归模型考察其波动趋势,提取其内在变化规律,并做出预测,为政府调整控制油价,企业制定生产决策,维持人们正常生活生产秩序提供参考。
关键词 :汽油价格,残差自回归模型,ARCH模型

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 研究背景
汽油与人们的生产和生活息息相关,同时作为国家稳定与发展的不可或缺的储备资源,每个国家都十分重视汽油市场的健康运行,包括需求、供给及价格等。《石油市场报告2019》指出,未来几年,世界石油市场会经历新的一轮的格局上的巨变,而与此相联系的汽油市场的需求供给也将发生调整,其中几乎可以肯定的是,发展中经济体的需求将继续增加,但需求增长速度会明显减缓。从国内来看,近年来,随着工业化与都市化进程推进及居民可支配收入的增加,加上环保政策的趋严,国内的汽油市场预期面临同国际相似的情形,但还需指出的是,国内汽油的消费需求结构也在发生着变化,消费重心会逐渐从传统的重工业部门转向日常消费需求,人们对汽油的需求量越来越大,其市场运作是否平衡,不仅关系到人们日常的生产生活,也关系到国民经济能否健康运行。邢孟冉 [1] 通过构建VAR模型从传导机制的角度说明了国际原油价格波动对我国物价的影响无论从理论上还是现实中都具有重要意义,晁江锋 [2] 基于动态随机一般均衡方法考察油价波动对我国宏观经济的动态影响,研究结果表明油价的上涨或下跌对企业的投资产出水平及资本存量等产生不可忽视的影响。
原油的储备又是有限的,这势必导致油价上升,油价的异常增长将会给人们的生活带来很多不便,对汽油加工企业的生产决策的制定也有很大影响,李登伟 [3] 等通过构建可持续发展评价指标体系对油价波动下油田企业的可持续发展进行探究,主要说明了油价下跌时油田企业应该及时应对,采取相应能效计划和管理措施。因此,通过构建拟合度较高的汽油价格模型,对汽油价格进行合理预测,对人们、企业及政府部门都具有一定程度的参考意义。
2. 文献综述
残差自回归模型是一种分析非平稳时间序列的研究方法,该模型在经济金融、人口增长、卫生等领域得到了广泛的应用。何慧 [4] 等通过残差自回归模型对四川人均GDP数据进行拟合,进行预测并与真实值对比后得出从模型中可以看到经济发展的规律或趋势并且完全有可能在今后相当长的时间内保持和发展;王丙参 [5] 等基于残差自回归模型对兰州市财政收入进行预测,通过与确定性分析、ARIMA模型拟合结果对比,说明残差自回归模型能够综合上述两种方法的优点,既能提高拟合精度,又便于解释;宋炜晔 [6] 等把残差自回归模型应用到旅游经济的研究中,得出了旅游市场的发展态势,对相关重要指标做了短期预测并提出可行性的建议与对策;刘晓冬 [7] 采用人口出生率时间序列数据,运用残差自回归模型分析和预测,结果表明人口出生率会延续下降趋势,这与我国现阶段贯彻的稳定低生育水平的政策是一致的;王璐 [8] 等发现残差自回归模型能较好地拟合艾滋病月度新发感染率的变动趋势,可为艾滋病新发感染情况的短期预测提供依据。
汽油价格变化有其客观必然性,翟丽萍 [9] 通过探究成品油定价问题对2015年的昆明市97#汽油价格做出了预测;徐凌 [10] 等结合定性分析,建立ARIMA模型对国际油价进行定量预测。
本文选取具有代表性的北京市近几年的汽油价格数据,运用残差自回归模型研究其内在变化规律,为政府、企业和人们进行决策提供参考。
3. 理论模型
3.1. 残差自回归模型
当序列显著地出现确定性趋势或者变化周期趋向固定时,首先考虑确定性因素分解方法,同时为了确保充分提取序列中的确定性信息,可以对残差序 的相关性进行检验。可以构造如下残差自回归模型 [11]:
。
3.1.1. 确定性模型拟合
对趋势效应 的拟合一般可以通过自变量为历史观测值或时间t的幂函数进行:
,或 。
3.1.2. 残差自相关性检验及拟合
对上述确定性拟合的效果进行检验,如果
即说明确定性模型拟合的程度不够。为了提取序列中残存信息,进一步提高模型拟合的精度,再次对残差序列进行拟合。
对残差的自相关性检验可以通过DW检验考察,如果DW检验显示残差序列高度自相关,我们进行残差序列的二次拟合。拟合步骤与ARIMA模型基本类似,由残差序列的偏(自)相关图的结果,对残差序列自相关系数和偏自相关系数的拖尾性或截尾阶数进行判断,残差序列的拟合结果由此可以得到。
3.2. 集群效应与ARCH模型
集群效应是这样一种现象,在确定性因素所导致的非平稳的影响被消除后,残差序列在部分时段存在持续偏大的波动,而在另一些时段存在持续偏小的波动。
从方差的角度来看,一旦出现集群效应,就意味着序列的方差在大部分时段是齐性的,但在某些时段方差与期望方差存在明显的差异。
我们使用ARCH模型:
通过采用LM检验(拉格朗日乘子检验)对残差平方序列构造q阶自回归方程,LM检验统计量为:
当上述统计量的P值小于 时,我们认为该序列存在非齐的方差,可以对残差平方序列中的自相关关系进行q阶自回归模型拟合。
4. 数据来源和处理
本文的数据来自北京市2013年~2018年的92#汽油调整日的价格,取自东方财富网(http://www.eastmoney.com/)数据中心的地区油价。
根据油价“十个工作日一调”规则和历史调整日的价格,下文中所使用的数据为月度数据,一个月记录两次,同时为保证数据结构的完整性,“缺失值”记录每月第10日和第25日的油价。
最终的数据包含140条观测值,对模型的拟合采用截至到2018年8月的136条观测值,2018年9月~10月4条观测值用来与通过模型预测的4期观测值做对比,说明模型拟合的效果。
5. 实证分析
5.1. 残差自回归模型
图1显示的汽油价格序列时序图,呈现出比较明显的先平稳后下降再上升的趋势。根据序列时序图的特点,对趋势效应的拟合分别采用自变量为时间t的三次函数和自变量为历史观测值的自回归模型。序列并没有明显的季节效应,故考虑建立如下的残差自回归模型:
。

Figure 1. Sequence diagram of 92# gasoline price from 2013 to 2018 (August) in Beijing
图1. 2013~2018 (8月)年北京市92#汽油价格序列时序图
5.1.1. 确定性模型拟合
(1) 时间t的幂函数为变量:
表1为分别采用lm函数和nls函数拟合关于t的三次函数回归模型,两个函数得到的拟合结果完全一致,t的一次方不显著,模型整体及其他变量都是显著的,所以对趋势效应的拟合模型则为:
。
Table 1. Fitting the cubic function regression model about t
表1. 拟合关于t的三次函数回归模型
(2) 1阶延迟 为变量:
表2为拟合关于1阶延迟序列值自回归模型的输出结果,模型整体及变量都是显著的,我们可以得到如下的确定性趋势拟合模型:
。
Table 2. Fitting autoregressive model for delay variable
表2. 拟合关于延迟变量的自回归模型
图2显示了两种拟合模型对趋势效应的拟合效果,星号标识为序列观察值,粗(红)线为关于时间t的三次函数拟合模型估计值,清晰的描述了序列的长期变化趋势,细(蓝)线为关于1阶延迟变量的自回归拟合模型估计值。
趋势部分已经拟合较为充分,下面来检验残差部分。根据图3中原序列拟合第一个趋势效应后的残差序列,时序图显示序列基本在0值附近上下浮动,并没有显示出任何明显的趋势或周期性,大体符合平稳的特征,我们暂时认为残差序列已平稳。
5.1.2. 残差自相关性检验及拟合
表3为拟合两个确定性趋势模型后残差序列DW检验结果,第一个确定性趋势模型DW统计量的值小于2,且P值极小,根据相关性判断标准,该模型拟合后的残差序列高度正相关。而对第二个模型而言,因为自变量和因变量具有自相关关系,所以需要使用Durbin h检验,DW统计量的值在2附近,说明残差序列不存在显著相关。

Figure 2. The fitting effect of two trend-fitting models
图2. 两个趋势拟合模型的拟合效果图
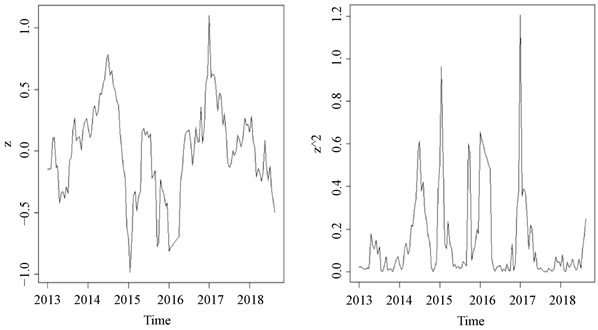
Figure 3. Residual and its square after the first trend effect
图3. 原序列拟合第一个趋势效应后的残差及其平方图
Table 3. DW-test on correlation of residual sequence
表3. 关于残差序列相关性的DW检验
通过对两个模型残差序列的LB检验,同样显示出第一个模型拟合后的残差序列高度正相关。为了充分提取相关信息,我们需要对第一个模型的残差序列再次进行信息提取。
根据图4表现出来的关于残差序列的自相关和偏自相关的性质,可以有如下结论:自相关系数拖尾,偏自相关系数1阶截尾,所以对残差序列拟合AR (1)模型。拟合结果为:
模型显著性检验(表4)表明该模型是显著的。

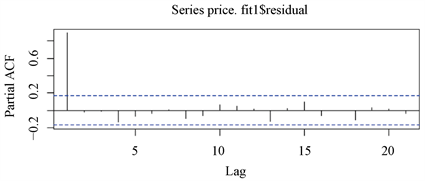
Figure 4. Autocorrelation and partial autocorrelation of residual sequence
图4. 残差序列的自相关图和偏自相关图
Table 4. Fitting the AR (1) model to the residual sequence
表4. 关于残差序列拟合AR (1)模型
此外,对上述1阶自回归模型进行DF检验,当特征根在单位圆内时,即 ,判定该残差序列平稳。
对拟合AR (1)模型后的残差序列进行白噪声检验,延迟6阶和延迟12阶两个LB统计量的P值(表5)显著大于显著性水平 ,所以该序列不能拒绝纯随机性的原假设,可以停止对该序列的统计分析。
Table 5. White noise test
表5. 白噪声检验
所以针对北京市2013年1月至2018年10月的92#汽油调整日的价格序列,我们构建了如下的残差自回归模型:
该模型对原序列的波动规律进行了比较直观地解释:北京市92#汽油价格在2013年1月至2018年10月大致服从一个时间t的三次函数的波动趋势。
由上述残差自回归模型预测出2018年9月和10月的北京市92#汽油价格数据如表6所示,相对误差控制在百分之十五以下,非常接近真实值。说明用残差自回归模型来对北京市2013年~2018年92#汽油价格研究的可信度颇有实用价值。
Table 6. Table of predicted values, true values and relative errors
表6. 预测值、真实值和相对误差表
5.2. 集群效应与ARCH模型
对趋势效应拟合关于时间t的三次函数后的残差时序图及残差序列平方图(图3)显示该残差序列没有表现出明显的非平稳特征,大部分时期波动范围在 之间。但是在2014年中,2015年前后,2016年前后,2017年前后,序列的波动很大,表现出集群效应特征。
通过LM检验考察残差平方序列是否纯随机,LM检验统计量的P值均小于显著性水平 ,拒绝原假设,认为该序列方差非齐。
在尝试过ARCH (3)和ARCH (2),这两个模型的参数检验结果均显示有参数不显著,直至ARCH (1)模型,检验结果显示模型显著(表7)。所以最后得到的拟合模型是ARCH (1)模型:
。
Table 7. ARCH (1) model for residual square sequence
表7. 关于残差平方序列拟合ARCH (1)模型
图5显示条件异方差模型拟合的置信区间(中间波动粗曲线)比无条件方差两条平行线给出的95%的置信区间更加符合原序列(中间波动细曲线)的真实波动情况。这说明条件异方差模型增加了对序列波动的预测的准确性。

Figure 5. Confidence interval comparison of conditional heteroscedasticity and homogeneity of variance
图5. 条件异方差置信区间和方差齐性置信区间比较图
通过对比AR (1)模型和ARCH (1)模型对残差序列进行拟合的结果,前者的相对误差明显要比后者的相对误差要小,而且通过信息准则比较也可以得出同样的结论,故就本文的数据来说,残差自回归模型拟合效果更好。
6. 结论
本文对北京市92#汽油价格进行的是短期预测,用残差回归模型拟合的结果比较理想,2018年10月、11月油价的预测值和真实值非常接近,而且从直观的序列波动规律显示汽油价格会有一个长期的增长趋势。但汽油价格受到多方面的影响,如经济增长、收入水平、欧佩克生产能力、汽油需求量等。本文没有考虑这些因素的作用,后续的研究方向是综合考虑这些因素分析油价的变动。需要指出的是,在油价的影响因素中,供求关系决定远期的价格走势,而政府干预等突发因素则直接影响近期价格,后续研究在进行短期预测时将充分考虑干预因素的影响。
文章引用
李小刚. 基于残差自回归模型的北京市92#汽油价格的分析与预测
Analysis and Prediction of 92# Gasoline Price in Beijing Based on Residual Autoregressive Model[J]. 社会科学前沿, 2019, 08(11): 1887-1895. https://doi.org/10.12677/ASS.2019.811257
参考文献
- 1. 邢孟冉. 国际原油价格波动对我国物价影响的传导机制研究[D]: [硕士学位论文]. 济南: 山东大学国际商务, 2018.
- 2. 晁江锋. 国际油价波动对我国宏观经济影响的研究——基于企业生产和居民消费视角的分析[J]. 价格理论与实践, 2018(3): 99-102.
- 3. 李登伟, 郑显林, 杨剑. 油价波动下油田企业的可持续发展能力研究[J]. 北京石油管理干部学院学报, 2018, 25(4): 52-56.
- 4. 何慧, 高登蕊, 冯长焕. 残差自回归模型的研究——基于四川省人均GDP的实证分析[J]. 兰州文理学院学报(自然科学版), 2014, 28(4): 30-32.
- 5. 王丙参, 魏艳华, 吴欣蔓. 基于残差自回归模型的兰州市财政收入预测与决策[J]. 天水师范学院学报, 2015, 35(2): 8-11.
- 6. 宋炜晔, 刘志媛, 王飞. 残差自回归模型在旅游经济当中的应用[J]. 现代商贸工业, 2018, 39(6): 23-25.
- 7. 刘晓冬, 姜宝法. 残差自回归模型在中国人口出生率预测中的应用[J]. 中国卫生统计, 2011, 28(3): 309-311.
- 8. 王璐, 杨书, 张强, 等. 残差自回归模型在艾滋病感染率变化趋势中的应用[J]. 预防医学情报杂志, 2013, 29(3): 175-177.
- 9. 翟丽萍. 基于回归分析的97号汽油定价问题[J]. 青年科学(教师版), 2014, 35(4): 211-212.
- 10. 徐凌, 黎佳卉, 李亮. ARIMA模型在国际原油价格预测中的应用[J]. 河南科学, 2013, 31(5): 692-695.
- 11. 王燕. 时间序列分析——基于R[M]. 北京: 中国人民大学出版社, 2017: 161-168.
