Statistical and Application
Vol.04 No.03(2015), Article ID:16057,12 pages
10.12677/SA.2015.43022
Research on the Price of Real Estate in China
—Based on e-TSVR Model and VAR Model
Lingling Xie, Yu Zhang
School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan
Email: xielingling1992@163.com
Received: Aug. 29th, 2015; accepted: Sep. 12th, 2015; published: Sep. 18th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
China’s price of real estate forecasts has been a hot livelihood issue, and scholars have paid much attention to it. In this paper, the monthly data of the national 2005-2013 years, in the study of China’s real estate prices, are based on the use of vector auto regression VAR model and support vector regression (e-TSVR) model, respectively to predict and compare the Chinese real estate prices. The results show that the average absolute error (MAE), the average absolute percentage error (MPE), the root mean square error (RMSE) value of the of e-TSVR model are less than VAR model, which shows that the e-TSVR model has better forecasting effects on the real estate prices in China.
Keywords:Real Estate Price, VAR Model, e-TSVR Model
中国房地产价格的研究
—基于e-TSVR模型和VAR模型
谢玲玲,张雨
云南财经大学统计与数学学院,云南 昆明
Email: xielingling1992@163.com
收稿日期:2015年8月29日;录用日期:2015年9月12日;发布日期:2015年9月18日

摘 要
中国的房地产价格的有效预测一直是民生的热点问题,从而备受国内外学者的高度关注。本文选用全国2005~2013年的月度数据,在研究中国房地产价格基础上,采用向量自回归(VAR)模型和支持向量回归(e-TSVR)模型,分别对中国房地产价格进行预测,并比较。研究结论表明:e-TSVR模型的平均绝对误差MAE、平均绝对百分比误差MPE、均方根误差RMSE值都小于VAR模型,说明e-TSVR模型对中国房地产价格的预测效果更佳,在房价的预测中有较强的科学性和可行性。
关键词 :模板房地产价格,VAR模型,e-TSVR模型

1. 引言
房地产业俨然已成为中国国民经济的支柱性产业,与经济发展,社会生产及其他经济活动紧密相关。在今天的中国,房地产行业带动了大量相关产业的迅猛发展。然而,随着房地产业的迅速发展,中国的房地产市场泡沫也越来越大,从而中国的房价波动烈,对中国经济的健康持续稳定发展有着重大不利的影响,同时,对人民群众的生活也而产生了较大大的影响作用。中国房价一直持续上升,加重了居民购房的负担。因此,对中国房地产价格进行预测不仅有利于房地产业与全面国民经济的持续、平稳、协调发展的实现,具有重要的现实意义,而且也已相当迫切。本文将利用历史数据构建合适的中国房地产价格预测模型,综合考虑影响因素对中国房地产的价格进行预测分析,以此判断未来中国房地产价格走势,成为当下房地产价格研究中的重要任务。通过构造正确的房地产价格预测模型,来判断未来的房地产业形势,稳定房地产价格,也就成为中国出台一系列调控房价的新政策的重要任务。
在房地产价格研究领域,王彬以北京房地产价格为研究对象,利用回归方程寻找影响房地产价格的主要因素,研究表明人均收入和投资额是其主要影响因素[1] ;罗玉波运用分位数回归研究影响房价的因素 [2] ;李勇、王有贵采用状态空间模型来分析影响中国房地产价格变动的主要因素 [3] ;李芳、李秋娟运用马尔柯夫区制转换模型的自回归模型(MS-VAR)选取2005~2012年人民币汇率和房地产价格的月度数据研究人民币汇率与房地产价格的互动关系 [4] 。在自回归模型的运用研究领域中,李成、马国校利用月度银行间同业拆借利率数据建立自回归模型研究我国银行同业拆借市场问题 [5] ;张卫平选取我国通货膨胀指数、货币量的季度数据,建立自回归模型以研究其在预测我国通货膨胀的有效性 [6] ;刘晓曙、郑振龙利用自回归模型验证商业银行的预测能力 [7] 。在支持向量回归的研究文献中,彭显刚、王洪森将双子支持向量回归模型运用在电力系统的负荷预测中 [8] ;曹慧运用支持向量回归机研究影响中国物价波动的主要因素 [9] ;鲍漪澜运用支持向量机研究金融时间序列,并对市场波动进行预测 [10] 。
本文主要选取2005~2013年月度住宅商品房平均销售价格数据,综合考虑影响中国房地产价格的主要因素,如利率、流动性过剩和国家财政预算收入。添加相关变量,利用e-双子支持向量回归模型和向量自回归模型对中国的房地产价格进行预测,并利用2013年1月~12月的相关数据进行验证,突出两个模型的预测效果。
2. 房地产价格影响因素
近几年,随着房地产价格日渐上升,房价涨幅迅速,给人民生活带来了沉重的经济负担和压力,影响了人民群众的生活水平,据此分析影响房价的因素,可以使得政府针对房地产行业采取切实有效的调控措施,以此实现房地产行业健康、持续、稳定的发展。
影响中国房地产价格的影响因素有很多,本文主要考虑3个影响因素:市场利率、国家财政收入和过剩流动性(EL)。
通过供给和需求两方面进行相互传导是利率变动对房地产价格的最主要影响方式。首先,利率变化会对房地产市场的需求产生直接影响,并且通过收入效应及替代效应两种转换方式完成。此外,就投资性需求或者投机性需求,利率上升时,由于贷款融资产生的财务费用加上因为转手产生的交易费用,房地产价格的上涨幅度必须存在一定程度的提高才能确保本金的收回。其次,在供给方面,利率直接反映了资金使用成本。若贷款利率不断增加时, 开发商的金融成本也随之增高,但在物价没有上升的情况下,资金的利息成本不能通过合理的方式转移到房价上, 房地产开发商的收益大幅减小,开发商就会控制对房地产的投资规模,导致房地产供给量下降。这样,利率的变化通过供需双方的传导间接地影响了房地产的价格。
过剩流动性全称是指“流动性资产过剩”,也就是流通中的的现金(M0)、狭义货币供应量(M1)及广义货币供应量(M2)等因素的过剩。简单的说,政府采取扩张性货币政策时,使货币供应量增加,从而导致利率下降,外币计价的存款收益高于国内本币存款的收益吸引力,本币贬值,国内房价与国外房价相比有所下降,国外资流进购置国内房产,增加了国内房地产需求,导致国内房地产价格上升。
国家财政收入主要分两部分,一部分是税收,另一部分是以土地为租让金为核心的资源性收益。所以,国家财政收入的高低直接影响房地产价格。
3. 模型介绍
3.1. e-双子支持向量回归(e-TSVR)
本文引入了一种新的支持向量回归方法,e-双子支持向量回归(e-TSVR)。e-TSVR将先求得两个函数:
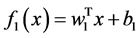 (1)
(1)
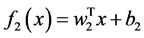 (2)
(2)
其中, 为输入向量,
为输入向量, ,
,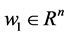 ,
, ,
, 且
且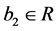 。由这两个函数的均值构成最终的回归函数,设一共有
。由这两个函数的均值构成最终的回归函数,设一共有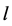 个训练样本,在计算
个训练样本,在计算 和
和 时,e-TSVR分别极小化成如下的经验风险函数:
时,e-TSVR分别极小化成如下的经验风险函数:
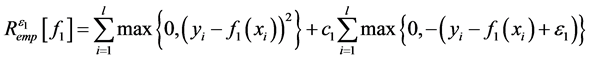 (3)
(3)
和
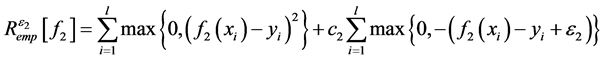 (4)
(4)
其中,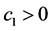 和
和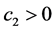 是参数,
是参数,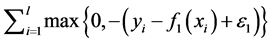 和
和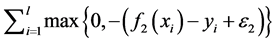 是损失函数。于是引入松弛变量
是损失函数。于是引入松弛变量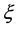 ,
,
 ,
, 和
和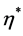 ,通过引入正则化项
,通过引入正则化项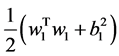 和
和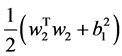 ,e-TSVR的原始最优化问题可以表示为:
,e-TSVR的原始最优化问题可以表示为:
 (5)
(5)
和
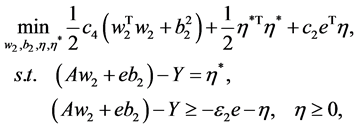 (6)
(6)
其中,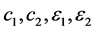 是正参数。
是正参数。
为解决式(5)和(6)的问题,需要得到它们的对偶问题。
关于(5)式的拉格朗日问题由下式给出:
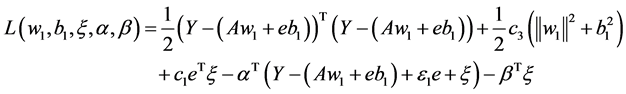 (7)
(7)
其中, 和
和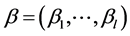 是Lagrange乘法式子的向量,
是Lagrange乘法式子的向量,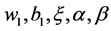 的条件由下式给出:
的条件由下式给出:
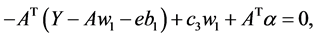 (8)
(8)
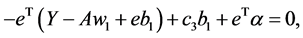 (9)
(9)
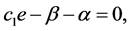 (10)
(10)
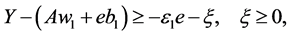 (11)
(11)
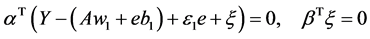 (12)
(12)
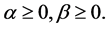 (13)
(13)
从式(9)中的 我们可以得出
我们可以得出 ,显然可以从式(7)和(8)中得出:
,显然可以从式(7)和(8)中得出:
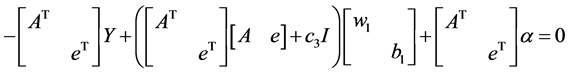 (14)
(14)
定义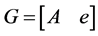 ,
,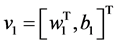 ,式(13)可以表示为:
,式(13)可以表示为:
 (15)
(15)
或者
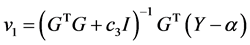 (16)
(16)
将式(16)运用K.K.T.的条件和拉格朗日公式,可以得到式(5)的对偶问题:
 (17)
(17)
当式(17)中的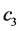 用
用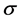 代替时,
代替时, 只是一个固定的正数,所以结构风险最小化原则不能在用
只是一个固定的正数,所以结构风险最小化原则不能在用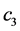 时完全反映出来。
时完全反映出来。
用同样的方法,将式(17)代入Lagrange函数,便得到了式(7)的Wolfe对偶问题:
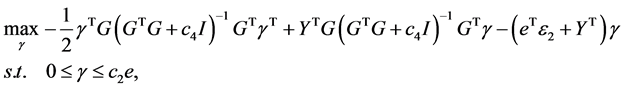 (18)
(18)
其中c是拉格朗日乘数,广义增量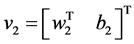 由下式可以得出:
由下式可以得出:
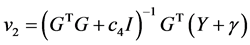 (19)
(19)
一旦从式(18)中求出式(5)和(6)的 和
和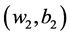 ,那么函数
,那么函数 和
和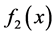 就可以求得解。那么估计的回归量构造如下:
就可以求得解。那么估计的回归量构造如下:
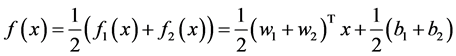 (20)
(20)
本文研究的中国房地产价格的数据是非线性的,由以下两个相近的函数:
 (21)
(21)
其中K是核参数,构建原问题如下:
 (22)
(22)
 (23)
(23)
其中,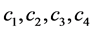 是正参数,用相同的方法可以得到其对偶问题,如下:
是正参数,用相同的方法可以得到其对偶问题,如下:
 (24)
(24)
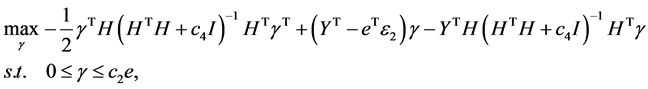 (25)
(25)
其中 ,那么广义向量
,那么广义向量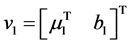 和
和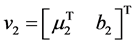 可以由下式得:
可以由下式得:
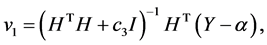 (26)
(26)
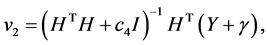 (27)
(27)
若计算出式(22)和式(23)中的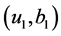 和
和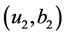 ,函数
,函数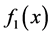 和
和 便可以获得,则构造如下估计的回归量:
便可以获得,则构造如下估计的回归量:
 (28)
(28)
3.2. VAR模型
在预测中国房地产价格方面,本文构建了VAR模型(向量自回归)来做预测研究。向量自回归模型(Vector Auto Regressive )是Sims在十九世纪八十年代提出的。VAR模型是研究多个相关的经济变量互动关系的常用模型,因而VAR模型用来预测相时间序列系统和随机干扰项对系统变量动态冲击的分析,然后理解不同经济冲击对经济变量产生的影响机制。
一般地,考虑一组时间序列变量: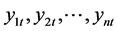 ,我们将其定义微
,我们将其定义微 维向量
维向量 :
:
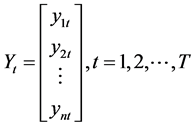 ,
,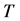 为总期数。
为总期数。
则滞后p阶的VAR模型形式为:
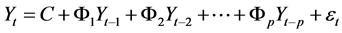 (29)
(29)
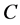 为
为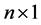 维常数向量,
维常数向量,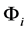 为
为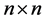 维自回归系数矩阵,
维自回归系数矩阵,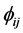 为其矩阵中的元素。
为其矩阵中的元素。 为
为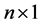 维白噪声序列,其中每个元素均是非自相关的。
维白噪声序列,其中每个元素均是非自相关的。
一个两变量且滞后期为1自回归模型形式为:
 (30)
(30)
其中,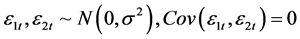 。
。
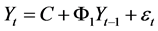 (31)
(31)
则滞后k期的模型为:
 (32)
(32)
VAR模型虽然看着比一般模型较为复杂,但是它的求解却不繁琐。常见的,VAR模型估计求解方法有最大似然估计(MLE)和最小二乘估计(OLS),最大似然估计和最小二乘估计求解得到的各参数是一致的。
4. 实证分析
4.1. 相关数据说明
本文选取的是2005~2013年的月度住宅商品房价格为因变量,样本点数量共为108个。数据来自2005年~2013年的中国统计年鉴。其中将2005年~2012年的月度数据,共96个样本点,用来进行模型的拟合。将剩下的12个样本点,2013年1月~12月的月度住宅商品房价格与用于模型预测的验证和比对。
自变量选取的是2005~2013年的月度过剩流动性和全国银行间同业拆借市场利率,国家财政收入。其中全国银行间的同业拆借市场利率可以从中国人民银行官网统计数据栏中获取。过剩流动性通常用广义货币供应量(M2)来表示。广义货币供应量(M2)和国家财政收入的全国月度数据均可从中国国家统计局统计年鉴中获得。
4.2. e-TSVR模型拟合
e-TSVR模型的预测本文选取的核函数为高斯核函数:
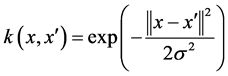
在运用e-TSVR模型回归时本文运用十折交叉验证的方法测试算法准确性。每次所做试验都会得到相应正确率。
预测时,本文利用2005~2012年月度的中国房地产价格、银行间同业拆借利率、M2货币供应量、国家财政收入数据进行分析,得到模型的拟合值和实际值,如图1。
对e-TSVR模型进行拟合准确度的定量分析,其中常用的判断拟合准确度的性能计算公式如下:
SSE (误差平方和):
SST (总平方和):
SSR (回归平方和):
NMSE (正则均方误差):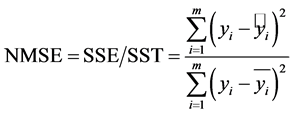
正则均方误差用来测量估计真实值与预测值之间的偏差。当NMSE值愈小时,预测的时间序列值与实际值愈接近,即预测效果愈好;NMSE值越大,则预测效果越差。
 (决定系数):
(决定系数):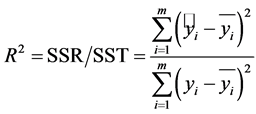
进一步对e-TSVR模型进行拟合准确度的定量分析,判断拟合准确度的性能计算公式的计算结果如表1。
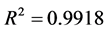 表明在房地产价格的总变差中,被估计的拟合方程所解释的比例为99.18%,即因变量(房地产价格)的99.18%可由模型确定。而且,如图1所示,e-TSVR模型下实际值和拟合值的曲线完全重叠,说明模型的拟合度非常高。
表明在房地产价格的总变差中,被估计的拟合方程所解释的比例为99.18%,即因变量(房地产价格)的99.18%可由模型确定。而且,如图1所示,e-TSVR模型下实际值和拟合值的曲线完全重叠,说明模型的拟合度非常高。
4.3. e-TSVR模型预测及结果分析
运用支持回归向量机构建模型,根据2013年1月~12月12个月度数据得到新的房地产价格的预测值,预测效果见图2。可见根据e-TSVR模型得到的拟合值与实际值非常接近,几乎在一条线上,预测效果非常好。
进一步对e-TSVR模型进行预测准确度的定量分析,判断预测准确度的性能计算公式的计算结果如表2。
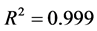 表明在房地产价格的总变差中,被估计的拟合方程所解释的比例为99.99%,即因变量(房地产价格)的99.99%可由模型确定。说明模型拟合度较高,预测效果非常好。
表明在房地产价格的总变差中,被估计的拟合方程所解释的比例为99.99%,即因变量(房地产价格)的99.99%可由模型确定。说明模型拟合度较高,预测效果非常好。
不管是拟合还是对未来房价的预测,e-TSVR模型得到的效果都非常好。
4.4. VAR模型拟合
运用VAR构建的模型,根据2005~2012年月度数据得到新的房地产价格的拟合值,拟合效果见图3。可见拟合值与实际值总体来说比较接近,拟合效果较好。
 表明在房地产价格的总变差中,拟合方程所解释的比例为92.9%,即房地产价格的92.9%可由模型所确定,可以看出方程的拟合度较高,见表3。
表明在房地产价格的总变差中,拟合方程所解释的比例为92.9%,即房地产价格的92.9%可由模型所确定,可以看出方程的拟合度较高,见表3。
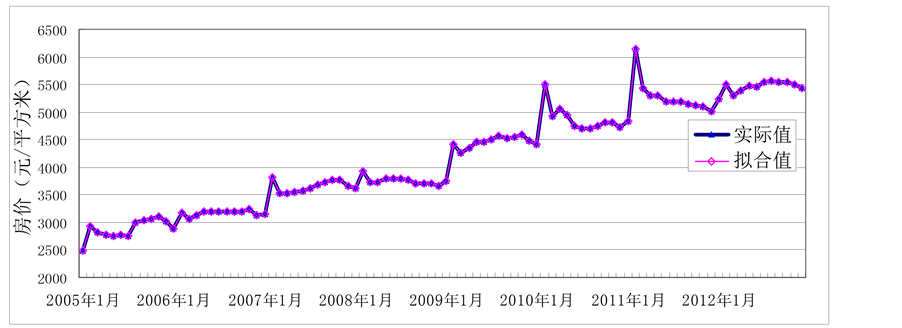
Figure 1. Price data of actual value and the fitting value comparison of e-TSVR model
图1. e-TSVR模型下房价数据实际值与拟合值比较

Figure 2. Price data of actual value and the predictive value comparison of e-TSVR model
图2. e-TSVR模型下的房价预测值与实际值比较
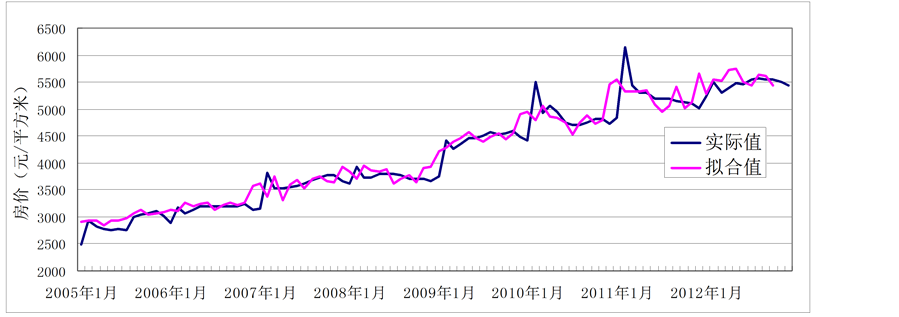
Figure 3. Price data of actual value and the fitting value comparison of VAR model
图3. VAR模型房地产价格实际值与拟合值比较
表1. 判断拟合准确度的性能公式计算值
表2. 判断预测准确度的性能公式计算值
表3. 判断拟合准确度的性能公式计算值
4.5. VAR模型的检验
进行Granger因果检验。平稳性检验能对每一个时间序列进行AR根检验。AR根检验需通过Eviews中的AR Roots Graph和AR Roots Table功能进行判断,若无特征根在单位圆外则序列平稳,则通过平稳性检验。
对收集得到的数据作AR根图如下。如图4可知,所有根的模的倒数都小于1,均位于单位圆内,说明该模型是稳定的,以此建立的VAR模型有效。
为了得出各变量之间是否存在互相影响的关系,此处进行Granger因果关系检验,显著性水平设为0.05,确定滞后期的值为2。检验结果如表4:
分析上表可以看出,利率、EI、财政收入变量的F统计量的概率P值均小于显著性水平5%,故拒绝原假设。表明利率、EI、财政收入变量会对房地产价格产生影响。
将房地产价格设为y,利率为变量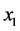 ,EI为
,EI为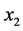 ,财政收入为
,财政收入为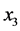 ,运用房价、利率、EI、财政收入数据后运行Eviews得到的VAR模型如下:
,运用房价、利率、EI、财政收入数据后运行Eviews得到的VAR模型如下:
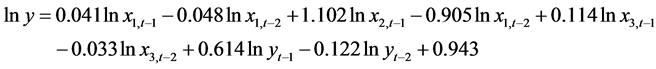
4.6. VAR模型预测及结果分析
运用VAR构建的模型,根据2013年1月~12月12个月度数据得到房地产价格预测值,预测效果见图5。可见预测值与实际值总体看不是很接近,预测效果不好。
本文进一步对VAR模型进行预测准确度的定量分析,其中常用的判断预测准确度的性能计算公式如表5。
 表明在房地产价格的总变差中,被估计的拟合方程所解释的比例为49.2%。即因变量(房地产价格)的49.2%可由模型确定。说明预测效果不理想。
表明在房地产价格的总变差中,被估计的拟合方程所解释的比例为49.2%。即因变量(房地产价格)的49.2%可由模型确定。说明预测效果不理想。
5. 结论
5.1. e-TSVR模型与VAR模型的比较分析
本文将对VAR模型和e-TSVR模型的预测效果进行比较。两个模型分别根据已知变量预测了2013年1~12月份的中国房地产价格,见图6。
图6中模型1预测值为VAR模型下的预测值,模型2预测值为e-TSVR模型下的预测值。从图6可以看出两个模型都可以较好的进行时间序列预测,但是e-TSVR模型预测的效果更接近实际值,因而e-TSVR模型预测效果更好。
进一步对两个模型进行预测准确度的定量分析,其中常用的判断预测准确度的性能计算公式如下:
MAE (平均绝对误差):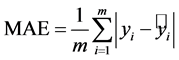
平均绝对误差利用了全部数据信息,因此能比较客观的反映变量分布的离散程度。MAE值越大,表示变量分布离散程度越大;MAE越小,则变量分布离散程度越小。
MPE (平均绝对百分误差):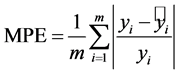
平均绝对百分误差是衡量模型好坏的一个指标。MAPE值越大代表预测值与原始值偏差越大,预测效果越差;MAPE值越小,预测值与原始值差别越小,也即预测效果越好。
RMSE (均方根误差):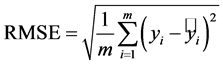
均方根误差也是衡量样本的离散程度的一个指标。RMSE值越大,说明离散程度越大;RMSE值越小,离散程度则越小。
据公式计算VAR和e-TSVR模型下相应的值,见表6。

Figure 4. AR root graph
图4. AR根图
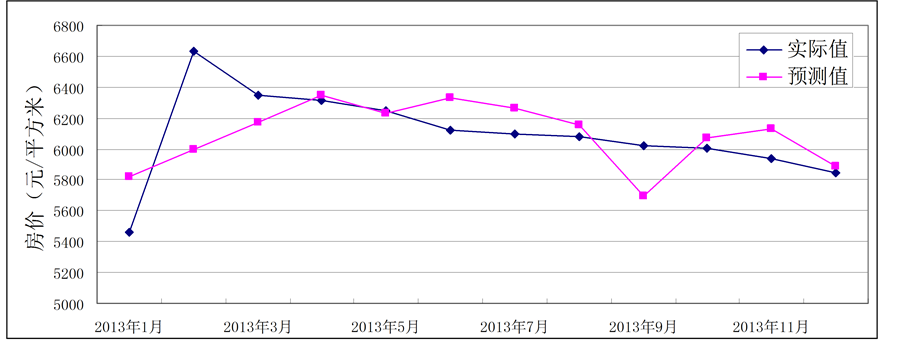
Figure 5. Price data of actual value and the predictive value comparison of VAR model
图5. VAR模型下的预测值和实际值的比较
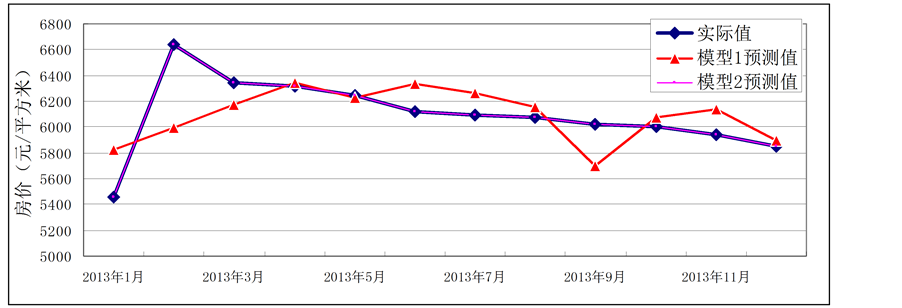
Figure 6. Comparison between the actual value and the predictive value of monthly house price based on VAR model and e-TSVR model in 2013
图6. VAR模型和e-TSVR模型下2013年月度的房价预测值与实际值比较
表4. Granger因果检验结果
表5. 判断拟合准确度的性能公式计算值
表6. VAR和e-TSVR各指标结果
从表中数据的对比可以看出在中国房地产价格的预测中,e-TSVR模型的MAE,MPE,RMSE值均远远小于VAR模型,e-TSVR模型对于在房地产价格的预测误差更小,说明e-TSVR比VAR模型拟合的效果更好。
5.2. 总结
本文在影响中国房地产价格的主要因素:利率、流动性过剩和国家财政收入的基础上,选取2005年1月至2012年12月的单月样本数据,分别采用向量自回归VAR模型和支持向量回归机e-TSVR模型,对中国2013年1月~12月房地产价格进行预测。研究结果表明:e-TSVR模型的平均绝对误差(MAE)、平均绝对百分比误差(MPE)、均方根误差(RMSE)值均小于VAR模型,说明e-TSVR模型比VAR模型具有更好的预测效果,预测结果更接近于实际值。
支持向量机是在统计学理论的基础上发展而来的借助于最优化方法来解决机器学习问题机器学习新方法,VAR模型和e-TSVR模型作为新型的支持向量回归机,都能很好的进行时间序列预测,但e-TSVR模型在预测方面比VAR模型效果更好。
致谢
本文是在云南财经大学统计与数学学院向其凤老师细心指导和建议下完成,在此对向其凤老师表示衷心的感谢!
文章引用
谢玲玲,张雨. 中国房地产价格的研究—基于ε-TSVR模型和VAR模型
Research on the Price of Real Estate in China—Based on ε-TSVR Model and
VAR Model[J]. 统计学与应用, 2015, 04(03): 196-207. http://dx.doi.org/10.12677/SA.2015.43022
参考文献 (References)
- 1. 王彬 (2007) 房地产价格影响因素分析. 硕士论文, 北京交通大学, 北京.
- 2. 罗玉波 (2011) 房价影响因素分析:分位数回归方法. 统计与决策, 6, 158-159.
- 3. 李勇, 王有贵 (2011) 基于状态空间模型的中国房价变动的影响因素研究. 南方经济, 2, 38-45.
- 4. 李芳, 李秋娟 (2014) 人民币汇率与房地产价格的互动关系. 国际金融研究, 3, 86-96.
- 5. 李成, 马国校 (2007) VAR模型在我国银行同业拆借市场中的应用研究. 金融研究, 5, 62-77.
- 6. 张卫平 (2012) 中国通货膨胀预测:基于AR和VAR模型的比较. 统计与决策, 4, 11-15.
- 7. 刘晓曙, 郑振龙 (2007) 商业银行VAR 模型预测能力的验证. 当代财经, 8, 39-43.
- 8. 彭显刚, 王洪森 (2014) 基于竞争ISPO双胞支持向量回归短期负荷预测. 电力系统及其自动化学报, 10, 46-68.
- 9. 曹慧 (2014) 基于支持向量回归机的中国物价波动影响因素探究. 硕士论文, 浙江工业大学, 杭州.
- 10. 鲍漪澜 (2013) 基于支持向量机的金融时间序列分析预测算法研究. 博士论文, 大连海事大学, 大连.
