Statistical and Application
Vol.04 No.04(2015), Article ID:16682,7
pages
10.12677/SA.2015.44032
A New Lifetime Distribution of System
—Mixture Exponential Poisson Distribution
Dongli Cui, Weiyan Mu
School of Science, Beijing University of Civil Engineering and Architecture, Beijing

Received: Dec. 9th, 2015; accepted: Dec. 27th, 2015; published: Dec. 30th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Lifetime distribution is a class of important matters in statistics, the parameter model of the lifetime distribution has the advantages of the mature theory, the simple calculation and the strong operation in practice. Therefore, we define a new lifetime distribution of system—the mixture exponential Poisson distribution based on the condition of the lifetime of the components and the number of the components subject to double parameters mixture exponential distribution and Poisson distribution, respectively. As a statistical model, we studied the various properties of the distribution, and discussed the maximum likelihood estimation of parameters under the condition of censored data of fixed number and time in this paper.
Keywords:Mixture Exponential Poisson Distribution, Maximum Likelihood Estimation, Lifetime Distribution

一种新的系统寿命分布
—混合指数泊松分布
崔栋利,牟唯嫣
北京建筑大学理学院,北京

收稿日期:2015年12月9日;录用日期:2015年12月27日;发布日期:2015年12月30日

摘 要
寿命分布问题是统计学中一类重要问题,寿命分布的参数模型具有理论成熟、计算简单、在实践中操作性强等优点。因此,我们定义了在元件寿命服从双参数混合指数分布、元件个数服从泊松分布的情况下的一种新的系统寿命分布——混合指数泊松分布,作为统计模型,研究了该分布的各种性质,且给出了在定数和定时截尾数据下参数的极大似然估计。
关键词 :混合指数泊松分布,极大似然估计,寿命分布

1. 引言
近年来,许多由经典的离散分布和寿命分布混合而成的新型寿命分布受到统计界以及其他领域的广泛关注,1998年Adimidis和Loukas将几何分布和指数分布结合,提出了指数几何分布(即Exponential- Geometric分布,简写为EG分布) [1] ,随后在2007年Coskun 提出了指数泊松分布(即Exponential-Poisson分布,简写为EP分布) [2] ,2009年Barreto和Criba提出了广义指数泊松分布(即广义Exponential-Poisson分布,简写为GEP分布) [3] 。2013年Nadaraja将几何分布、泊松分布和指数分布结合,获得了几何指数泊松分布(即Geometric Exponential Poisson分布,简写为GEP分布) [4] ,2015年,陈庆华提出了混合指数几何分布(即Mixture Exponential-Poisson分布,简写为MEP分布),并研究了该分布的各种性质,讨论了参数的极大似然估计 [5] 。
在上述研究成果的基础上,我们将指数分布延伸到双参数混合混合指数分布,并与泊松分布结合,定义了新的寿命分布——混合指数泊松分布,并研究了该分布的各种性质,给出了三种情况下参数的极大似然估计。
混合指数泊松分布可描述为如下模型:考虑一个由 个原件组成的串联系统,其中各个原件独立工作,N是服从泊松分布的随机变量,元件的寿命服从双参数混合指数分布,则系统寿命服从混合指数几何分布。
个原件组成的串联系统,其中各个原件独立工作,N是服从泊松分布的随机变量,元件的寿命服从双参数混合指数分布,则系统寿命服从混合指数几何分布。
2. 混合指数泊松分布的定义
若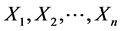 是服从双参数混合指数分布且相互独立的随机变量,
是服从双参数混合指数分布且相互独立的随机变量,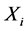 的密度函数为
的密度函数为
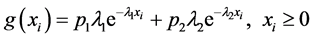 ,
,
其中,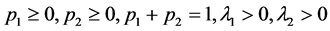 。所以
。所以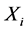 的分布函数为
的分布函数为
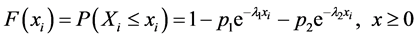 。
。
假设N服从泊松分布,其概率分布列为
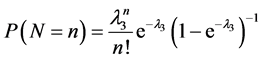 ,
,
其中, ,且N和
,且N和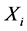 相互独立。令
相互独立。令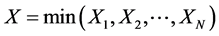 ,则X关于N的条件分布函数为
,则X关于N的条件分布函数为
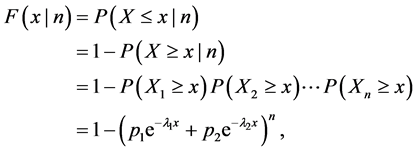
令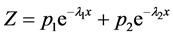 ,所以X的边缘分布函数为
,所以X的边缘分布函数为
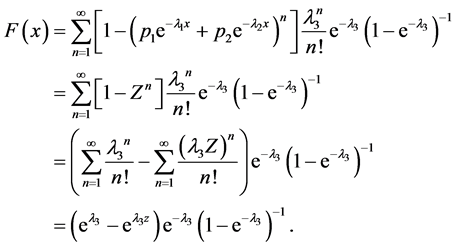 (1)
(1)
X的边缘密度函数为
 (2)
(2)
这样,由混合指数分布和泊松分布结合,得到了一个新的复合分布。
若非负随机变量X的分布函数形如(1)式,(或者说密度函数形如(2)式),则X服从混合指数泊松分布,记为 ,
,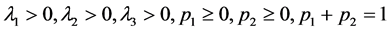 。
。
3. 混合指数泊松分布的性质
3.1. 密度函数的单调性
对于任意的参数值,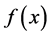 是关于x的减函数,且
是关于x的减函数,且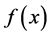 在
在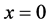 处取得最大值为
处取得最大值为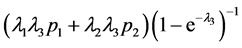 ,当
,当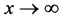 时,
时, 趋近与0,符合寿命分布,可以当
趋近与0,符合寿命分布,可以当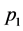 或
或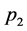 等于0时,混合指数泊松分布退化为指数泊松分布(EP分布) [2] 。
等于0时,混合指数泊松分布退化为指数泊松分布(EP分布) [2] 。
3.2. 分位数
设随机变量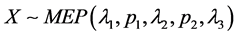 ,当
,当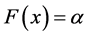 时,则有
时,则有
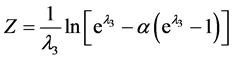 ,
,
特别地,当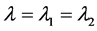 时,此分布的
时,此分布的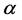 分位数为
分位数为 ,中位数为
,中位数为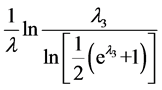 。
。
证明: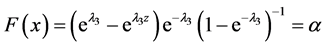 ,可计算得出
,可计算得出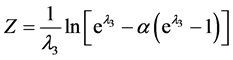 ,当
,当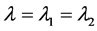 时,
时,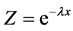 ,
,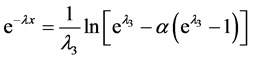 ,有
,有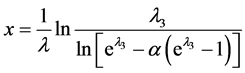 ,即此分布的
,即此分布的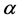 分位数为
分位数为 ,中位数为
,中位数为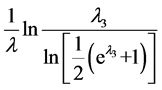 。
。
3.3. 期望与方差
设随机变量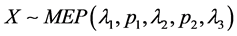 ,则X的期望和方差分别为
,则X的期望和方差分别为
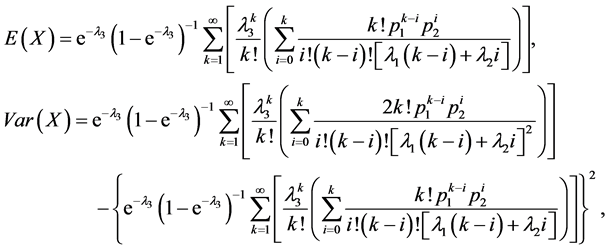
证明:由X的分布函数为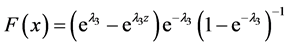 ,可以得到
,可以得到
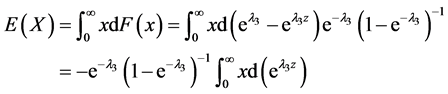 。
。
令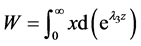 ,
,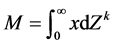 ,则
,则 ,根据泰勒公式,可以得到
,根据泰勒公式,可以得到
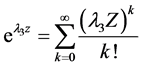 ,则
,则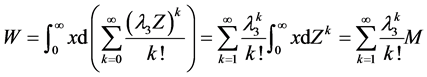 ,所以最终把
,所以最终把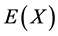 转化为求M。而
转化为求M。而
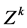 可以写成如下形式
可以写成如下形式
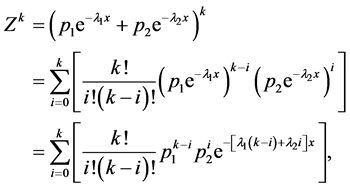
所以根据上式,给出M的如下形式
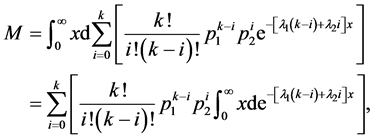

所以X的期望为
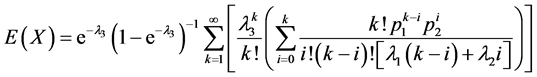 。
。
又因为
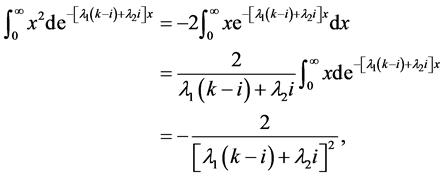
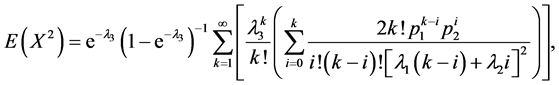
利用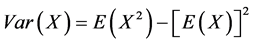 ,即可得出混合指数泊松分布的方差。
,即可得出混合指数泊松分布的方差。
3.4. 生存函数与风险函数
设随机变量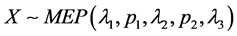 ,
,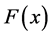 为其分布函数,
为其分布函数,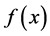 为其密度函数,则
为其密度函数,则
1) 生存函数(或可靠度函数)为 [6]
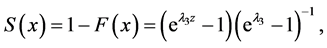
2) 风险函数为 [7]
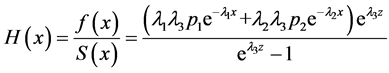
4. 混合指数泊松分布下的参数估计
设总体的概率函数为
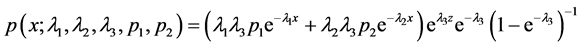 ,
,
其中 是未知参数,
是未知参数,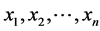 是来自该总体的样本,样本的联合概率函数用
是来自该总体的样本,样本的联合概率函数用 表示,即样本的似然函数为
表示,即样本的似然函数为
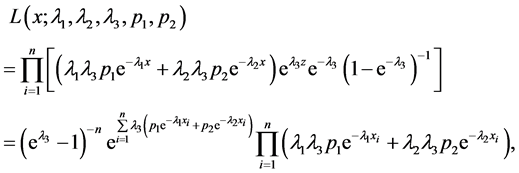
所以对数似然函数为
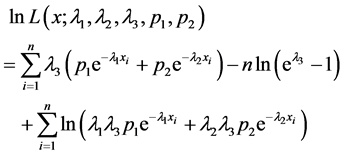
对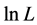 分别求关于
分别求关于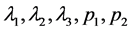 的偏导数,并令其为0,得到似然方程组为如下
的偏导数,并令其为0,得到似然方程组为如下
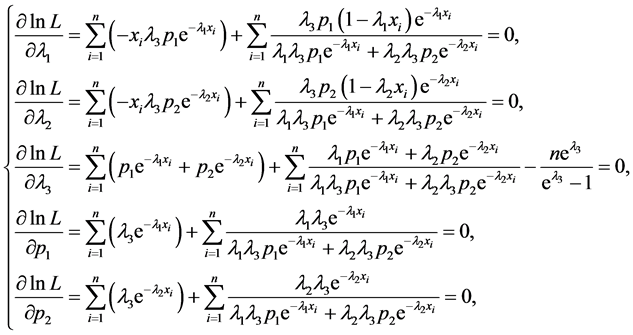
在已知观测数据后,解上述方程组,即可得出参数的极大似然估计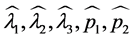 。
。
4.1. 定数截尾数据下对参数的估计
设样本容量为n,截尾个数为 ,记k个观察到的寿命的次序统计量为:
,记k个观察到的寿命的次序统计量为: ,令他们的观察值依次为
,令他们的观察值依次为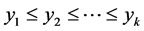 ,则此时的似然函数为
,则此时的似然函数为
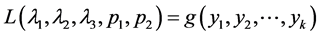 ,
,
前k个次序统计量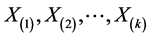 的联合密度函数为
的联合密度函数为
 ,
,
特别的,当 时,
时,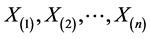 的联合密度函数为
的联合密度函数为
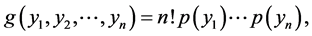
令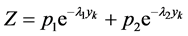 ,所以似然函数为
,所以似然函数为

再次按照极大似然估计的步骤即可求出定数截尾数据下参数的极大似然估计 [8] 。
4.2. 定时截尾数据下对参数的估计
设样本容量为n,指定的时间长度设为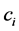 ,寿命数据设为
,寿命数据设为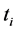 ,第i次观测从0时刻起,当观测的寿命
,第i次观测从0时刻起,当观测的寿命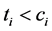 时,寿命记为
时,寿命记为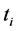 ,如果到
,如果到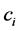 时刻还未观测到寿命数据,则记
时刻还未观测到寿命数据,则记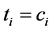 ,
,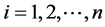 。对n个观测数据
。对n个观测数据 ,其中有些是寿命数据,有些是截尾数据,记寿命数据的集合为D,截尾数据集合为C [9] 。所以
,其中有些是寿命数据,有些是截尾数据,记寿命数据的集合为D,截尾数据集合为C [9] 。所以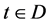 时对应的概率函数为:
时对应的概率函数为:
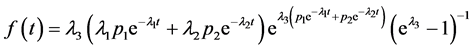 ,
,
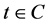 时对应的概率函数为:
时对应的概率函数为:
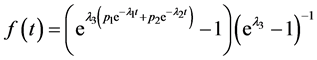 ,
,
因此 的似然函数为:
的似然函数为:
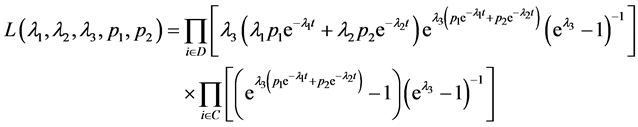
再次按照极大似然估计的步骤即可求出定时截尾数据下参数的极大似然估计[10] 。
文章引用
崔栋利,牟唯嫣. 一种新的系统寿命分布—混合指数泊松分布
A New Lifetime Distribution of System—Mixture Exponential Poisson Distribution[J]. 统计学与应用, 2015, 04(04): 289-295. http://dx.doi.org/10.12677/SA.2015.44032
参考文献 (References)
- 1. Adamidis, K. and Loukas, S. (1998) A Lifetime Distribution with Distribution with Decreasing Failure Rate. Statistics and Probability Letters, 39, 35-42. http://dx.doi.org/10.1016/S0167-7152(98)00012-1
- 2. Kus, C. (2007) A New Lifetime Distribution. Computational Statistics and Data Analysis, 51, 4497-4509. http://dx.doi.org/10.1016/j.csda.2006.07.017
- 3. Barreto-Souza, W. and Cribari-Neto, F. (2009) A Generalization of the Exponential-Poisson Distribution. Statistics and Probability Letters, 79, 2493-2500. http://dx.doi.org/10.1016/j.spl.2009.09.003
- 4. Nadarajah, S., Cancho, V. and Ortega, V. (2013) The Geometric Ex-ponential Poisson Distribution. Stat Methods, 22, 355-380. http://dx.doi.org/10.1007/s10260-013-0230-y
- 5. 叶立淼, 陈庆华. 混合指数几何分布[J]. 统计研究, 2015, 32(7): 106-108.
- 6. 王林书. 几种新寿命分布类[J]. 应用数学学报, 2004, 27(3): 397-399.
- 7. 杨元启. 寿命分布的参数估计[J]. 科技风, 2013(21): 31-32.
- 8. 程侃. 寿命分布类与可靠性数学引论[M]. 北京: 科学出版社, 1999: 1-3.
- 9. 茆诗松, 王玲玲. 可靠性统计[M]. 上海: 华东师大出版社, 1984: 1-2.
- 10. 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 北京: 高等教育出版社, 2006: 1-3.