Statistics and Application
Vol.06 No.05(2017), Article ID:23244,7
pages
10.12677/SA.2017.65065
Test for the Homogeneous Poisson Process Model of Highway Traffic Flows
Ya’nan Li, Shuhe Lei*, Fenglin Sun
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong
*通讯作者。
Email: *lyn_stat@163.com
Received: Dec. 7th, 2017; accepted: Dec. 22nd, 2017; published: Dec. 29th, 2017

ABSTRACT
In order to build a traffic model of vehicles arrival times of highway, using the observed traffic data, a stochastic point pattern is composed by recording vehicles arrival times. Based on the theory of spatial point process, the Ripley’s K function is applied to one-dimensional stochastic point process. According to the characteristics of Homogeneous Poisson Process, a graphical approach is proposed to test Homogeneous Poisson Process combined with envelope test. And the effectiveness of the test is verified by simulation. Then the graphical approach is applied to the patterns, and the result indicates that arrival times of vehicles composed a Homogeneous Poisson Process. Finally, the traffic model of Chang-Tai freeway is obtained by estimating the parameter of the Homogeneous Poisson Process.
Keywords:Homogeneous Poisson Process, Traffic Flows, K Function, Envelope Test
高速公路交通流量的齐次泊松过程模型检验
李亚楠,类淑河*,孙丰霖
中国海洋大学数学科学学院,山东 青岛
Email: *lyn_stat@163.com
收稿日期:2017年12月7日;录用日期:2017年12月22日;发布日期:2017年12月29日
摘 要
为检验高速路上车辆到达时刻是否服从齐次泊松过程模型,使用实测的交通数据资料,记录车辆到达监测点的时间,构成一个随机点过程。基于空间点过程的理论,将Ripley的K函数应用到一维随机点过程中,依据齐次泊松过程情形下K函数的特殊形式,结合包络检验,提出了一种齐次泊松过程的图形化检验方法,并通过随机模拟验证了检验方法的有效性。使用该图形化方法对车辆到达常台高速监测点的时间所构成的点过程进行检验,结果表明该点过程是一个齐次泊松过程,通过估计其参数得出常台高速该时段车流量的齐次泊松过程模型。
关键词 :齐次泊松过程,交通流量,K函数,包络检验

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
当前,我国城市高速发展,交通问题成为城市发展过程中面临和需要解决的重要难题之一。随着经济水平的不断提高,居民机动车保有量持续上升,再加上高速公路网越来越发达,选择长途自驾出行的居民日益增加。为解决交通拥堵,及时处理高速公路交通安全问题,做好高速公路车流量的实时监控,掌握车流量的变化是非常必要的。在实际应用中,研究者们通常使用简单的概率分布——泊松分布来描述交通流量的分布情况。
国内学者对于泊松分布在交通流中的应用研究有很多,郭冠英 [1] 提出了三种常用的车辆到达分布,正常情况下车流量为泊松分布,车流出现持续的拥挤现象时为二项分布,当车流行驶受到周期性干扰时用负二项分布来刻画效果更好。莫智锋 [2] 等在微观交通仿真的研究中,首先说明了交通仿真断面的发车规律满足无后效性、平稳性、普通性,然后根据实测数据估计参数,建立了基于泊松分布的断面发车模型;丁春蕾 [3] 假设高速公路上行驶的车辆到达收费站的过程为泊松过程,从而建立了高速公路收费站的排队模型;张蓉 [4] 等通过分析北京某路口的实际车流量的分布规律,得出该路口车流符合泊松分布的结论,并进一步阐述了不同交通特征的概率分布函数在交通仿真中的应用。
以上研究的研究对象都是统计分布,实际上交通流应该被视为一个随机点过程。随机点过程是一类特殊的随机过程,因为随机事件的发生在数学上可用一个理想化的点来表示。于是,一个按一定的统计规律在某空间中随机分布的点集就形成一个随机点过程。齐次泊松过程是最简单、常用的随机点过程。交通流数据作为点过程是动态的、随机的,通常情况下应该是泊松过程,在短时间内可以认为是一个齐次泊松过程。但是,给定一个实际的观测数据,是否能够确认它是一个泊松过程,迄今为止还没有太多研究。在使用泊松过程来刻画车辆到达时刻时,研究者们通常是假设交通流服从泊松分布,通过估计参数直接建立模型,然而,必不可少的应该是首先对交通流是否服从泊松分布进行检验。邓永录 [5] 给出了几种检验齐次泊松过程的方法,薛珊荣 [6] 从统计分布的角度出发,假设给定的交通流资料服从泊松分布,记录每分钟来车辆数并记录出现该车辆数的频数,使用不同方法进行了检验,根据泊松分布的期望和方差相等的特性,计算监测数据的均值和方差并比较二者的差距;比较理论频数与实际频数的差距;以及泊松分布的χ2拟合优度检验,通过这些方法验证了泊松分布对监测数据是适合的。此外,由于齐次泊松过程的发生时间间隔服从指数分布,因此也可以检验车辆到达时刻间隔是否服从指数分布。
除了上述所说的方法之外,近二十年来空间统计学的兴起使得空间点过程的理论逐渐得到广泛应用,也为我们提供了更有效的点过程检验工具,这些工具基于K函数、L函数、G函数等等。Ripley的K函数 [7] 是用来分析事件发生位置数据的工具,表示以过程中的任意一点为中心,r为半径的区域内的期望点数与随机点过程密度的比值,它是一个关于距离r的函数,对于齐次泊松过程,K函数表示的是这个区域的测度。本文利用交通实测视频与数据共享平台 [8] 中城际快速路G15w常台高速2012年3月28日8:00~9:42的交通流数据,对数据进行处理后获得车辆到达时刻的点过程样本,基于Ripley的K函数和蒙特卡罗模拟,采用包络检验的方法,验证了此点过程为齐次泊松过程,从而建立了常台高速公路交通流的齐次泊松过程模型。
2. 理论与方法
2.1. 空间点过程与Ripley的K函数
随机点过程按照空间维数来划分,可以分为一维点过程和空间点过程,一维点过程对应时间轴上的点过程,空间点过程中的点表示研究对象发生的位置。
空间点过程是数据分析中非常有用的统计模型,点过程的均值以及更高阶的矩是研究其特征的重要工具,特别是强度测度和二阶矩测度,以及由它们所产生的K函数、G函数、成对相关函数等导出量 [9] 。其中Ripley的K函数常用来分析空间点过程的随机性。
将事件的发生看作是二维平面中的点,定义
(1)
其中,λ表示点过程的密度,Nr(x)表示以点过程中固定的一点x为中心,半径为r的圆内的点数,即到x的距离小于等于r的点过程中的点数,则λK(r)表示对任一x,在B(x,r)这个圆内的期望点数。
特别地,齐次泊松过程具有平稳性、普通性和独立增量性等特性。二维平面中的齐次泊松过程的理论K函数有如下形式:
(2)
这是由于齐次泊松过程作为增量平稳的计数过程,其强度参数与平均发生率相等,也就是点过程的密度。这样,式(1)中的期望即为 ,整理后可得式(2)。此时K函数是关于r的二次函数,根据样本数据,可以求出点过程样本的K函数估计值。记点过程为Φ,观测区域为W,在W内,将Φ中的点 依次作为特征点,给定距离r,计算到特征点的距离为r的过程中的点数,将所有的点数加起来,除以特征点的总数之后,再除以过程的密度,密度即单位区域内的点数,表示如下:
(3)
其中 ,n表示过程中总点数,A(W)表示观测窗的面积。
将Ripley的K函数应用到一维点过程φ中,设已知点过程φ在 上有n个点发生时,它们的发生时间为 ,对于任一x,式(1)中Nr(x)表示区间 中φ的点数,则λK(r)的含义就是在δ(x, r)这个邻域内的期望点数。基于式(3)可得点过程φ的K函数估计为:
(4)
其中 ,L为观测区间的长度。
特别地,若点过程为齐次泊松过程,那么发生时间 就是 上的均匀分布的独立同分布样本的一个重排,也就是所谓的完全随机点过程。与二维上的结论类似,一维齐次泊松过程的K函数也有着特殊的形式:
(5)
基于式(5)可知,一维情形下K函数只是一个关于r的线性函数,记齐次泊松过程的K函数为 。如果待检验的过程是齐次泊松过程,那么该过程的K函数应与 一致或者相差甚微,但是怎样一种程度算相差甚微是无法定义的,于是在此基础之上,使用包络模拟的图形化方法来检验一个随机点过程是否为齐次泊松过程 [10] [11] 。
2.2. 图形化检验方法
假设点过程φ是强度参数为β的齐次泊松过程,β未知。首先,通过极大似然估计的方法来估计模型的参数,不妨设在一固定时间区间 上对点过程进行观测。假若在 中观测到的随机事件总数为n,它们的发生时间依次 ,于是 ( )可以看作是参数为β的指数分布随机变量的n个独立观测。则这n个观测的似然函数是
(6)
将式(6)的右端对β求导后令其等于零得出β的极大似然估计
(7)
因此,齐次泊松过程作为具有平稳性、普通性的随机点过程,它的强度可由平均发生率也就是密度来估计。由式(7)选择强度参数为 的齐次泊松过程模型,从该模型中模拟s条新的样本数据,对于每一条模拟样本,估计其K函数,令 和 ( )分别表示原始数据和模拟数据的K函数估计值,由于K函数的变化范围较大,为了使结果更加清晰直观,使用理论的K函数 对 标准化,记
(8)
则 ,并定义上下包络为:
(9)
(10)
检验方法为在同一坐标内作出 、 以及得到的包络 与 四条函数曲线,在原假设成立的情况下, 与 的差距应是很小的,即 应在 附近,同时如果 落在包络之外,则否定原假设,认为点过程φ不是齐次泊松过程。此方法无法预先给定犯第一类错误的概率,只能后验地在模拟中估计出来。根据不等式:
, (11)
得到犯第一类错误的概率为1 − (m/s),其中m表示使得不等式(11)成立的过程数量。
2.3. 随机模拟
根据齐次泊松过程的事件发生时间间隔服从指数分布的特性,借助R语言产生一组指数分布的随机数,这里不妨令强度参数为10,假设观测区间为[0,50],整理得到一个齐次泊松过程。根据上述图形化检验方法,取s = 499,根据式(4)分别估计它们的K函数,由式(8) (9)得到上下包络。结果如图1所示,该点过程的K函数估计恰好落在包络线以内,所以认为此点过程为齐次泊松过程。同样地,对上述过程重复500次,得到通过检验次数为486,未通过检验次数为14,因此犯第一类错误的概率为0.028。这表明该方法对于检验齐次泊松过程是有效的。
3. 实证分析
以城际快速路G15w常台高速2012年3月28日上午8:00~9:42的交通流数据为案例来建立该路段的齐次泊松过程模型。该数据采用的交通流实测方法是视频录像调查法,将所拍摄的录像转换成逐帧排列的图像文件,一秒为一帧,对于每一帧图像,进行图像识别,为识别到的车辆编号,记录帧号、位置、车头时距、车辆类型及所在车道,按照预先设定好的时间间隔取得下一帧图像,根据同编号车辆的移动距离获得该车的行驶速度 [12] 。本文仅选用2车道的监测数据,2车道为正常行驶车道。基于每辆车在监测区域中的位置p、速度v及帧号m,由
(12)
可以计算出每辆车进入监测区域的时间t,以此便得到了一个点过程数据样本,记为X。这里假设任意时刻车辆的到达均不受其他车辆的影响,且每个时刻最多有一辆车到达,显然这个假设是合理的。
记初始时刻为零,单位时间为每分钟,则常台高速的车流量数据是在时间区间[0 min, 102 min]上的离散时间点。过程中的点的总数n为551,观测区间长度L为102 min,根据齐次泊松过程的参数估计,由式(7)可知,其强度参数的估计即为密度的估计,求得强度 约为5.4。
所以,如果原假设成立,则认为点过程X是强度为5.4的齐次泊松过程。取包络模拟中的s为499,即产生499条强度为5.4的齐次泊松过程样本数据,通过R语言实现随机模拟,并分别计算其K函数估计值: ,由式(8)得出 ,并根据式(9)、式(10)取出上下包络线,作图如图2所示。观察图2可以发现, 恰好落在包络线之内,而且始终靠近0刻度线,这说明 与齐次泊松过程的理论K函数值相差甚微,由不等式(11)计算得出犯第一类错误的概率为0.04,因此有理由相信点过程X
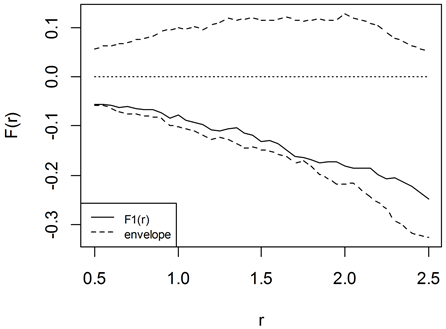
Figure 1. The envelope test of Homogeneous Poisson Process
图1. 齐次泊松过程的包络模拟检验图

Figure 2. The envelope test of the arrival times in Chang-tai Highway
图2. 常台高速车辆到达过程的包络模拟检验图
就是一个齐次泊松过程。所以,常台高速此路段的车辆到达时刻模型是一个强度参数约为5.4的齐次泊松过程。基于齐次泊松过程的特性,在微观交通仿真时,通过产生同参数β的指数分布,即可获得发车时间间隔,从而得出此路段在某一时段的发车模型,用于交通管理与决策。
4. 结论与讨论
基于空间点过程理论中Ripley的K函数,得到了一种齐次泊松过程的图形化检验方法。这种方法直接对随机点过程进行检验,无需将其转化成对统计分布的检验,而且能够直观地展现检验结果,齐次泊松过程的理论K函数值是检验的重要参考,模拟的包络曲线是检验的强有力依据。但是同时这种检验方法也有一定的局限性,就是无法预先给定犯第一类错误的概率,尽管可以后验地从模拟中估计出来,但是仍然不知道计算该假设检验问题的p值的方法,这仍需进一步地研究和改进。从结果来看,使用齐次泊松过程来描述常台高速此路段在该时间段内的车辆到达过程是合理的,而且能够估计出点过程的强度,对应着交通流量和密度的大小,这将是解决交通问题、有效利用道路资源的依据。但是应当指出的是,并不是所有的交通流都是齐次泊松过程,本文仅选用了一个时间段的数据,对于其他时间、其他路段是否还有同样特性并没有做太多研究。一天中可能会出现高峰期与低峰期,这就意味着车辆到达时刻的点过程的强度是不同的,即可能为非齐次泊松过程,像交通拥堵或者交叉口附近的交通流都不能用齐次泊松过程来描述。
基金项目
本项目由国家自然科学基金(41276010),教育部博士点专项基金(20130132130002)支持。
文章引用
李亚楠,类淑河,孙丰霖. 高速公路交通流量的齐次泊松过程模型检验
Test for the Homogeneous Poisson Process Model of Highway Traffic Flows[J]. 统计学与应用, 2017, 06(05): 576-582. http://dx.doi.org/10.12677/SA.2017.65065
参考文献 (References)
- 1. 郭冠英. 交通工程普及讲座第九讲交通量的到达分布[J]. 华东公路, 1983(5): 63-73.
- 2. 莫智锋, 余嘉, 孙跃. 基于泊松分布的微观交通仿真断面发车数学模型研究[J]. 城市交通, 2002(4): 4-6.
- 3. 丁春蕾. 高速公路交通流量数学模型与分析[D]: [硕士学位论文]. 天津: 天津大学, 2003: 4-7.
- 4. 张蓉, 石建军, 任福田, 等. 数理统计知识在交通仿真中的部分应用[J]. 北京工业大学学报, 2003, 29(4): 473- 476.
- 5. 邓永录, 梁之舜. 随机点过程及其应用[M]. 北京: 科学出版社, 1992: 106-109.
- 6. 薛珊荣. “泊松分布”在交通工程中的应用[J]. 公路, 1981(1): 26-30.
- 7. Dixon, P.M. (2006) Ripley’s K Function. Encyclopedia of Environmetrics, 3, 1796-1803.
- 8. 郭明旻. 交通实测视频与数据共享平台[EB/OL]. http://traflow.fudan.edu.cn/instr.html, 2017-04-05.
- 9. Baddeley, A. (2007) Spatial Point Processes and Their Applications. Stochastic Geometry, 1, 1-75.
- 10. Stoyan, D. and Penttinen, A. (2000) Recent Applications of Point Process Methods in Forestry Statistics. Statistical Science, 15, 61-78.
- 11. Grabarnik, P., Myllymäki, M. and Stoyan, D. (2011) Correct Testing of Mark Independence for Marked Point Patterns. Ecological Modelling, 222, 3888-3894. https://doi.org/10.1016/j.ecolmodel.2011.10.005
- 12. 许谦, 郭明旻, 吴正. 嘉兴两条城际高速公路车速测量与统计研究[J]. 水动力学研究与进展, 2014, 29(3): 325-331.