Statistics and Application
Vol.07 No.01(2018), Article ID:23953,7
pages
10.12677/SA.2018.71010
Time Series Analysis of China’s Price Level
Xu Huang
Economic Statistics, Yunnan University of Finance and Economics, Kunming Yunnan
Received: Feb. 9th, 2018; accepted: Feb. 21st, 2018; published: Feb. 28th, 2018

ABSTRACT
This paper analyzes the CPI index of China from 1985 to 2014 by using time series measurement model. First, the data is analyzed in a stationary manner. It is found that the sequence has an increasing trend through the sequence diagram, so the sequence is a non-stationary sequence [1] . The sequence is processed by logarithmic process and the first order difference is made. The basic stability is found by the sequence diagram after the difference. Then the ARIMA(p,d,q) model is fitted to the stationary sequence. The fitting effect test and the heteroscedasticity test of the model are carried out [2] [3] . Finally, the fitting model is used to predict the CPI data of the next 5 years. It can be seen from the prediction results that the CPI is still increasing.
Keywords:CPI Index, ARIMA(p,d,q) Model, Forecast
关于我国物价水平的时间序列分析
黄旭
云南财经大学经济统计学,云南 昆明
收稿日期:2018年2月9日;录用日期:2018年2月21日;发布日期:2018年2月28日

摘 要
文章通过运用时间序列计量模型对我国1985~2014年的CPI指数进行分析,首先对数据进行平稳性分析,通过时序图发现序列有递增的趋势,所以序列为非平稳序列 [1] ,再对序列做对数化处理并做一阶差分,通过差分后的序列时序图发现基本平稳,之后对平稳序列做ARIMA(p,d,q)模型拟合,并对模型进行拟合效果检验和异方差检验 [2] [3] ,最后用拟合后的模型预测2015~2020年的CPI数据。从预测结果看出CPI仍然呈递增趋势。
关键词 :CPI指数,ARIMA(p,d,q)模型,预测

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 研究背景、意义及目的
消费者价格指数(CPI),是一个反映居民家庭一般所购买的消费价格水平变动情况的宏观经济指标 [4] 。它是度量一组代表性消费商品及服务项目的价格水平随时间而变动的相对数,是用来反映居民家庭购买消费商品及服务的价格水平的变动情况 [5] 。居民消费价格统计调查的是社会产品和服务项目的最终价格,一方面同人民群众的生活密切相关,同时在整个国民经济价格体系中也具有重要的地位。它是进行经济分析和决策、价格总水平监测和调控及国民经济核算的重要指标。其变动率在一定程度上反映了通货膨胀或紧缩的程度。一般来讲物价全面地、持续地上涨就被认为发生了通货膨胀。
2. 模型介绍
具有如下结构的模型称为求和自回归移动平均模型,简记为ARIMA(p,d,q)模型:
式中, ; ,为平稳可逆ARMA(p,q)模型的自回归系数多项式; ,为平稳可逆ARMA(p,q)模型的移动平滑系数多项式。
求和自回归移动平均模型这个名字的由来是因为d阶差分后序列可以表示为:
式中, ,即差分后序列等于原序列的若干序列值得加权和,而对它又可以拟合自回归移动
平均(ARMA)模型,所以称它为求和自回归移动平均模型。ARIMA模型的实质就是差分运算与ARMA模型的组合。这说明任何非平稳序列如果能够通过适当阶数的差分实现差分后平稳,就可以对差分后序列进行ARMA模型拟合了。
经济时间序列的平稳性检验
大部分时间序列是非平稳的,这类序列的数字特征是随着时间的变化而变化,难以通过序列已知的信息去掌握时间序列整体的随机性。对于非平稳的时间序列,当然可以通过差分运算得到平稳序列,因此首先应对时间序列进行平稳性检验,检验的标准方法是采用单位根检验,这里对单位根检验采用ADF检验。其模型为:
(1)
(2)
(3)
假设检验:
原假设说:序列存在一个单位根;备择假设说:不存在单位根序列。通过ADF值与在一定的显著性水平下的临界值的比较,就可判断序列的平稳性,如接受原假设,则存在单位根即是非平稳;如拒绝原假设,则序列是平稳的。
3. 数据来源
数据来自国家统计局1985~2014年全国CPI指数(1978 = 100)。时序图如图1。
4. 实证分析
4.1. 数据处理
从上图可以肯出CPI指数有明显的上升趋势,即原数据是非平稳数据。首先对数据做对数化处理并做时序图如图2。
从图2中可以看出序列依旧有明显的递增趋势,在对对数化后的数据做一阶差分并作时序图如图3。
从图3中可以看出序列基本平稳。
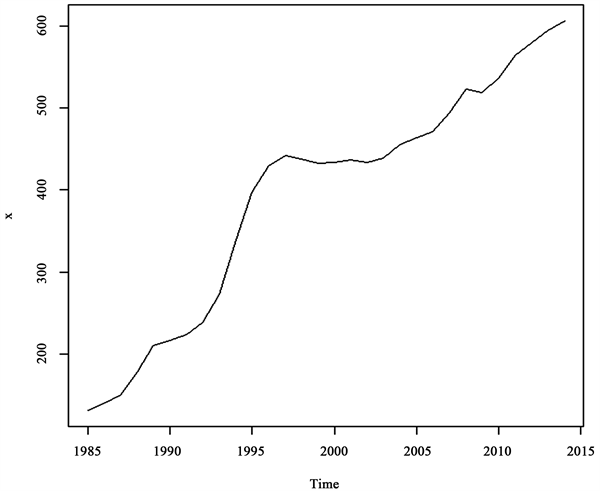
Figure 1. 1985-2014 national CPI index (1978 = 100)
图1. 1985~2014年全国CPI指数(1978 = 100)
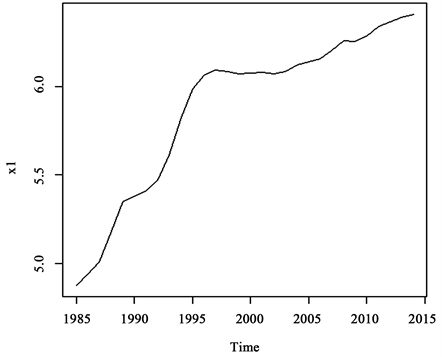
Figure 2. 1985-2014 data on the logarithmic data of the national CPI index
图2. 1985~2014年全国CPI指数对数化数据
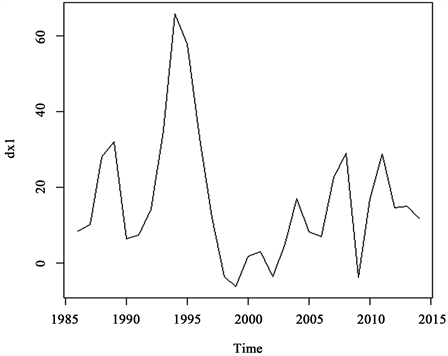
Figure 3. First order difference data
图3. 一阶差分数据
4.2. 随机性检验
对差分数据采用LB统计量进行白噪声检验,使用延迟6阶和延迟12阶的LB统计量,延迟6阶的检验统计量P值为0.03091 < 0.05的显著性水平,所以拒绝原假设,即序列存在6阶以内的短期相关,即序列是平稳非白噪声序列。
4.3. 平稳性检验
对差分后序列做自相关图和偏自相关图观察序列的短期相关性,并对差分后的序列做单位根检验以判断差分序列的平稳性。
从ACF图(图4)中可以看出序列存在一节自相关,从PACF图(图5)中可以看出序列存在一节的偏自相关,但从图中读出的结果存在一定的主观性,所以后面采用auto.arima函数自动定阶建立模型。对差分后的序列做单位根检验结果如下。
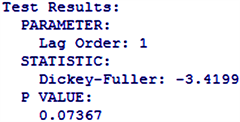
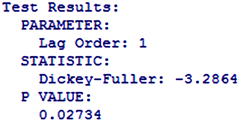
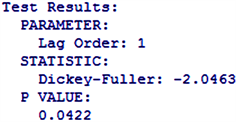
从上图中可以看出差分序列在三个模型中均在P为0.1的显著性水平下,拒绝原假设,所以一阶差分序列为平稳序列。

Figure 4. ACF inspection figure
图4. ACF检验图
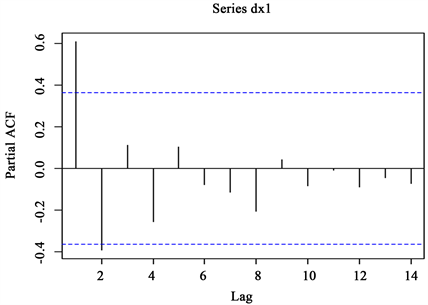
Figure 5. PACF inspection figure
图5. PACF检验图
4.4. 模型拟合
采用auto.arima()函数对差分序列及原序列自动拟合,对原序列拟合结果为arima(0,1,1),对差分后序列拟合结果为arima(0,0,1),拟合结果相同进一步证明一阶差分序列为平稳序列。结果如下。
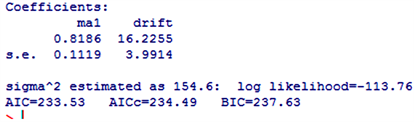
从结果可以看出模型为arima(0,1,1),与图形观察的结果不同,所以图形是有主观成分在里面的,对模型的参数进行显著性检验,其P值小于0.05的显著性水平,所以参数是显著的。
模型为
4.5. 模型的显著性检验
模型的显著性检验是对模型的残差序列做白噪声检验,若模型的拟合结果好那么残差序列为白噪声序列,即残差序列没有相关性,模型对序列信息提取充分。反之若残差序列为非白噪声序列则模型拟合效果差,序列信息为被充分提取。对残差序列做延迟6阶和12阶的白噪声检验,结果p值为0.8599和0.9829均大于0.05的显著性水平,所以接受原假设即残差序列为白噪声序列。对残差序列做6阶和12阶的异方差检验P值分别为0.331和0.7443,均大于0.05的显著性水平,所以残差序列不存在异方差。
4.6. 预测
由拟合的模型效果较好,所以对2015~2020年的CPI数据做预测结果如下。

预测曲线图如下图6。
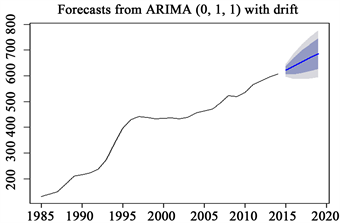
Figure 6. CPI forecast for 2015-2020
图6. 2015~2020年CPI预测图
5. 结论
从模型预测结果可以看出未来CPI依旧会呈现上升趋势,目前我国CPI快速增长的原因有以下几条:一是国际大宗商品价格快速上涨,传导进入国内导致我国相关产品价格快速上涨,如:铁矿石、黄金等等。二是人民币不断升值,导致热钱快速大量的流入国内,按照我国货币政策,外国货币需在流入过程中将其储备起来,这部分流入的货币将会兑换成“同价值”的人民币在国内流通,国内货币过多导致货币购买力下降、物价上涨。三是国民消费增长趋势明显增快,近几年经济的高速增长必然带动了巨大的国民消费能力,而强劲的出口也会提高企业的效益和就业岗位,国家对农民的扶持政策,让农民的收入明显增长,这些因素累积起来将共同促进消费增长。政策建议:一、国家的宏观调控,国家为抑制通货膨胀而采取的宏观政策,在改善经济过热和对通货膨胀的语气上起到了举足轻重的作用。所以国家的宏观调控必不可少。二、加强监管投机炒作,镇府对期货市场炒作行为应该加强监管。
文章引用
黄旭. 关于我国物价水平的时间序列分析
Time Series Analysis of China’s Price Level[J]. 统计学与应用, 2018, 07(01): 72-78. http://dx.doi.org/10.12677/SA.2018.71010
参考文献 (References)
- 1. 张鹤. 时间序列分析方法在粮食价格指数分析中的应用[J]. 统计与决策, 2004(9): 32-34.
- 2. 李可柏, 陈森发. 南通地区月降水量时间序列分析[J]. 数理统计与管理, 2009, 28(3): 555-565.
- 3. 汤润龙, 颜春莲, 张曙光. 红塔香烟月均价格的时间序列分析[J]. 数理统计与管理, 2005, 24(1): 10-14.
- 4. 刘颖, 张智慧. 中国人均GDP (1952-2002)时间序列分析[J]. 统计与决策, 2005(2X): 61-62.
- 5. 姜弘. 居民消费价格指数的时间序列分析及预测[J]. 统计与决策, 2009(4): 117-118.