Statistics and Application
Vol.
08
No.
01
(
2019
), Article ID:
28672
,
13
pages
10.12677/SA.2019.81010
Discussion and Research on the Prediction of House Price in Shenbei New District of Shenyang City
Shuang Wang, Congdian Cheng
School of Mathematics and Systems Science, Shenyang Normal University, Shenyang Liaoning
Received: Jan. 7th, 2019; accepted: Jan. 21st, 2019; published: Jan. 28th, 2019

ABSTRACT
We discuss the effects to predict the trend of house price on Shenbei New Districtof Shenyang City, based on the house price data of a building in the district, respectively by the polynomial fitting method and Markov Chain method. Through a long-term follow-up statistics of the house price data on the building, repeated forecasting and empirical testing, it is concluded that the two forecasting methods are more suitable for predicting the trend of house price in the district and the effects are largely same. In addition, the method of weighted Markov Chain forecasting on house price given by Gu Ying and Xia Letian has been improved and perfected. The work we have done in this article can promote the development of the research on regional house prices.
Keywords:House Price, Forecast, Fitting, Weighting, Markov Chain
关于沈阳市沈北新区房价预测的探讨与研究
王双,程丛电
沈阳师范大学数学与系统科学学院,辽宁 沈阳
收稿日期:2019年1月7日;录用日期:2019年1月21日;发布日期:2019年1月28日

摘 要
基于沈阳市沈北新区某楼盘房价数据分别探讨用多项式拟合方法和加权马尔可夫链方法预测沈北新区房价走势的效果。通过长期跟踪统计房价数据,反复预测与实证检验,得出了这两种预测方法都较适用于预测沈阳市沈北地区房价走势且效果大体相同的结论。此外,还改进与完善了顾莹和夏乐天所给出的加权马尔可夫链房价预测方法。所做工作对于促进区域房地产研究的发展具有一定意义。
关键词 :房价,预测,拟合,加权,马尔可夫链

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
由于房地产业是提高人民的住房水平,实现“居者有其屋”,形成和谐社会的基本条件,所以世界上各个国家的政府都非常重视国民的住房问题。发达国家早在工业革命期间就已开始研究居民的住房问题,如恩格斯早在19世纪就曾写过《关于住房问题》的专著。我国房地产业在上世纪九十年代初起步,至今也已有30多年的历史了。这些年里,我国建筑、建材、家具、家电、装饰、设计、金融、化工、机电、钢铁、塑料等行业的快速发展都与房地产业的蓬勃发展密切相关。据不完全统计,我国40余个行业的发展都与房地产业有着直接或者间接的联系,房地产业也一跃成为了我国的重要支柱型产业。由于房地产市场的规模宏大,关联产业多,且是城市化的主要载体,又直接影响着国计民生,因此房地产业受到了国内外的广泛研究。例如,辛杰 [1] 就我国国民经济与房地产业如何相互协调发展和提升这一问题展开了探讨与研究。张慧 [2] 论述了目前中国房地产的现状以及房地产业对中国经济的刺激作用。王国军、刘水杏 [3] 借助投入产出模型分析了房地产业与其相关产业关联关系的变化规律。何志华 [4] 运用VAR模型来分析相关房地产业的联动性,结果表明房地产业与建筑、金融、机械、建材、化工等行业整体上具有长期均衡关系。
房地产业的发展,不仅与整个国民经济的发展密切相关,而且与区域经济息息相关。我国的房地产市场往往是按照不同区域进行划分的,一般情况下,在短期内区域经济会随着房地产市场的波动而变化,房地产业的稳定发展会间接地提高当地人民的经济水平和生活质量。因此,近年来国内不少学者开始致力于区域房地产业的研究,尤其是关于一些城市的房地产价格问题的研究。阎秋序 [5] 根据其自身经验讨论了我国区域经济发展与房地产业之间的关系,并提出了促进房地产行业与区域经济协调发展的方法。顾莹,夏乐天等 [6] 建立了一种利用加权马尔可夫链模型预测房价的方法。江跃勇 [7] 从多方面影响房价的因素出发通过灰色系统理论和马尔可夫链理论相结合的方法对成都市各个区域房产价格进行了预测性研究,结果有效地反映了成都市房价的变化趋势。王昱博等 [8] 运用马尔可夫链方法预测武汉市短期内房价的涨跌情况为近期内急于买房的市民提供了重要的参考。刘娜娜等 [9] 发展了一种基于网络搜索词利用多项式回归模型预测成都市商品房价格为购房者提供参考价格的方法。
沈阳市沈北新区对于沈阳市的发展具有重要意义。目前,就我们所知,尚且没有学者认真地研究过沈北新区房价走势预测问题,特别是,虽然现有文献中已给出不少预测区域房价的方法,但是究竟什么样的方法较适合用于沈北新区房价预测依然是一个值得探讨的问题。上述动态暨空白激发我们从事该项研究。本文试基于笔者近几年来所收集的沈阳市沈北新区某楼盘房价数据,探讨与研究运用多项式拟合方法与加权马尔可夫链模型方法预测沈北新区房价走势的问题。
2. 情况说明
沈阳市沈北新区是连接辽宁、吉林、黑龙江和内蒙古四省区的黄金通道和“东北城市走廊”的枢纽重地。改革开放以来,沈北新区通过利用得天独厚的地理优势、资源优势,全方位实施外向牵动、改革驱动、科教拉动和合力推动四大战略,使全区经济和社会各项事业都取得了长足的发展。沈阳市市委副书记曾经指出,“十一五”期间,沈阳提出要进入全国副省级城市第一集团军,也就是进入前五名,目前沈阳市名列第八,想跨过前面的哪一位,都将十分艰难,能否实现此目标关键取决于沈阳四大空间的发展情况,其中相对落后的沈北地区是最具有战略性的空间,也是辽宁最具发展潜力的区域。沈北地区的崛起,将成为沈阳全面振兴的动力引擎,使沈阳实现一个新的跨越。
房地产业是沈北新区的主要产业,与沈北的发展密切相关,探讨其走势与研究沈阳市经济的运行密切相关。
为了研究沈北新区房价走势,近年来我们跟踪搜集了沈阳市沈北新区的房价数据。表1便是我们所跟踪搜集到的沈阳道义街区某楼盘2016年9月~2018年1月逐月房价的数据。
Table 1. The house price and its status of the A building in the moral block A in the month of September 2016 to January 2018
表1. 道义街区A楼盘2016年9月~2018年1月逐月房价及其状态
由图1可以看出,A楼盘的房价在2017年3月以前走势平稳,没有太大变化;但在2017年3月以后,房价逐步提升。整个沈北新区房价大概如此。
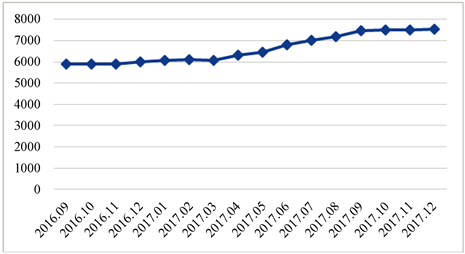
Figure 1. A real estate in Daojie District, Shenbei New District, September 2016 to December 2017
图1. 沈北新区道义街区A楼盘2016年9月~2017年12月房价走势图
3. 多项式回归预测
基于沈北新区A楼盘逐月房价数据,参考文献 [10] [11] 的方法,寻找多项式拟合回归模型,并做预测。
1) 根据A楼盘2016年9月~2017年8月逐月房价数据,寻找多项式拟合回归模型,并预测2017年9月房价。
分别记月份为x,房价为y,预测值为z。利用matlab软件进行多项式拟合,发现这一阶段的房价较符合二次多项式拟合回归模型,其拟合曲线图像如图2所示。
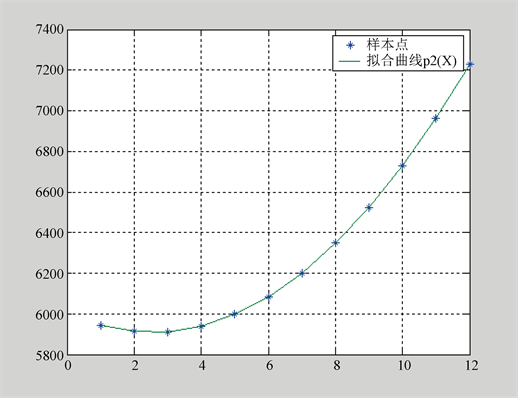
Figure 2. Based on building A September 2016-August 2017 Quadratic fitting Curve Image of House Price
图2. 基于A楼盘2016年9月~2017年8月逐月房价的二次拟合曲线图像
由上述结果可得二次拟合回归方程为 ,将 代入上述方程得2017年9月的预测房价约为 元/平方米。实际房价为7465元/平方米,每平方米相差55元。
2) 依次根据A楼盘2016年10月~2017年9月,2016年11月~2017年10月,2016年12月~2017年11月,2017年1月~2017年12月的逐月房价数据,运用1)中方法预测接下来四个月2017年10月,2017年11月,2017年12月,2018年1月的房价。
所得预测结果依次为:7825.9元/平方米,7938.1元/平方米,7917.6元/平方米,7808元/平方米。
实际房价依次为:7500元/平方米,7499元/平方米,7530元/平方米,7565元/平方米。
绝对偏差依次为:325.9元/平方米,439.1元/平方米,387.6元/平方米,243元/平方米。
3) 说明与讨论
表3中定义了实际房价与预测房价之绝对偏差的级别。从表2和表3可以看出,在这五次预测中,有一次预测值与实际值的绝对偏差为允许偏差,三次为接受偏差,一次为较大偏差,可以说准确率达到了80%。由此可知,上面所采用的多项式回归预测方法基本适用于预测沈阳市沈北新区房价的走势。
Table 2. Example of house price forecast value, actual value and absolute deviation sum
表2. 实例中房价预测值、实际值与绝对偏差汇总
Table 3. Absolute deviation corresponding level partitioning
表3. 实例中绝对偏差对应级别划分
4. 加权马尔可夫链预测
传统的马尔可夫链预测没有充分考虑各个数据之间相关关系的强弱,没有充分地利用历史数据中隐藏的信息,往往预测结果不尽如人意。鉴于马尔可夫链预测方法的这种不足,近年来许多学者都在探讨如何改进,加权马尔可夫链方法就是其中一种,参见文 [6] ,这种方法的好处在于充分利用了数据间的强弱关系,使已有数据资料的信息最大化被利用,使得预测结果更加准确合理。本节我们适当改进文 [6] 的方法,并讨论用其预测沈北新区房价走势的效果。
4.1. 方法介绍
设 ,为连续n个度量期的房价,可用加权马尔可夫链方法预测第 个度量期的房价,具体方法请见文 [6] 中2.3节。需要说明的是,在文 [6] 中,顾莹和夏乐天是用系统聚类–离差平方和法进行状态分类的,这种方法不是唯一的,实用中可以用其它方法进行分类。
下面我们通过基于A楼盘2016年9月~2017年8月连续12个月的房价预测2017年9月的房价来介绍与改革文 [6] 的方法。
4.1.1. 分类
先根据A楼盘2016年9月~2017年8月连续12个月房价的具体情况,用表4定义类别,然后再依表5给出这段时间里每月房价的类别。
Table 4. A partitioning of housing price states
表4. A楼盘房价状态区间划分
Table 5. A property price index and its corresponding status from September 2016 to August 2017
表5. A楼盘2016年9月~2017年8月房价指数及对应状态
4.1.2. 马氏性检验
在房价预测中,马氏性检验是应用马尔可夫链预测的前提,只有通过了马氏性检验,才可以用马尔可夫链方法进行预测。
用文 [6] (或文 [12] )的方法对 A楼盘2016年9月~2017年8月连续12个月的房价进行马氏性检验。
设房价 的状态为 (这里, )。通过令
其中,m为状态的个数(这里 ),做出一步转移概率矩阵 ,再命 ,且 ,则当n较大时有近似的统计量 。计算 ;
给定显著性水平 ,查表得分位点 。由于 。该楼盘房价数据序
列符合马氏性,所以可以运用相关的方法和原理进行预测分析。
注:实际计算中可能遇到 的情况,这时在运算中把 当作0来处理,这样做是合理的,
原因如下。
,
其中 ,由此可知当 时,必有 ,将 视为无穷小量,则: ,
所以这样做是合理的。
4.1.3. 计算出各阶自相关系数
,(这里 )
其中, 为滞时是k个时期的自相关系数,K为要计算的最大阶数, 为房价的均值。结果见表6。
4.1.4. 规范化
,
结果见果表6,其意义见文献 [6] 。
Table 6. Summary of results of normalization of autocorrelation coefficients by order in examples
表6. 实例中各阶自相关系数规范化结果汇总
4.1.5. 求各步转移概率矩阵
仿照文献 [6] 的方法求出一步,二步,三步和四步转移概率矩阵,结果如下。
4.1.6. 求转移概率
基于 (初始月)时点的房价状态 , (这里 ),用频率方法求 时点房价为状态i的概率 ,简记为 。结果如表7所示。
4.1.7. 预测
命 ,用其作为 时点房价状态为i的概率;然后找出满足 的状态i*,以其作为 时点房价的预测状态。在当前情况下,i* = IV。
由表7可知,最大加权概率和为1,相应的状态为IV,即用此方法预测该楼盘2017年9月房价的状态为IV,也就是说此时的房价应满足: 。根据我们的跟踪结果,该楼盘在2017年9月的实际房价为7465元/平方米,该房价正好处于状态IV,说明预测结果准确。
Table 7. A housing prices forecast for September 2017
表7. 2017年9月A楼盘房价的预测
4.2. 方法检验
运用上述方法,依次基于A楼盘2016年10月~2017年9月连续12个月的房价预测2017年10月的房价,基于A楼盘2016年11月~2017年10月连续12个月的房价预测2017年11月的房价,基于A楼盘2016年12月~2017年11月连续12个月的房价预测2017年12月的房价。预测结果状态依次为:IV,IV,IV;实际房价状态依次为:IV,IV,IV。准确率达到100%,由此可见加权马尔可夫链预测方法适于用来预测沈阳市沈北新区该楼盘的房价。
5. 总结
本文首先汇报笔者两年多来对于沈阳市沈北新区某楼盘房价跟踪情况,然后基于这些统计数据研究用多项式拟合模型方法预测沈北房价走势的效果与用加权马尔可夫链方法预测沈北新区房价走势的效果。
通过用多项式拟合方法反复预测并将预测价格与实际价格进行比较,结果表明五次预测中,有一次预测值与实际值的绝对偏差为允许偏差,三次为接受偏差,一次为较大偏差,此结果说明该方法有效程度较高,适用于预测沈北地区房价走势。通过运用加权马尔可夫链方法反复预测并与实际价格进行比较,结果表明在四次预测中预测状态全部与实际房价状态一致。这个结果说明该方法适用于预测沈北地区房价的走势。
两种方法相互比较,多项式拟合方法的预测结果是具体数值,但是吻合程度不是特别好,五次预测中仅一次绝对偏差是允许偏差,三次为接受偏差,一次为较大偏差;虽说加权马尔可夫链方法的预测结果是状态,但预测结果都与实际相同,所以两种预测方法效果大体相同。
讨论如何有效预测沈阳市某区域的房价是一个有着重要意义的研究课题,衷心希望本文工作能够促进该项研究的发展。
文章引用
王 双,程丛电. 关于沈阳市沈北新区房价预测的探讨与研究
Discussion and Research on the Prediction of House Price in Shenbei New District of Shenyang City[J]. 统计学与应用, 2019, 08(01): 84-96. https://doi.org/10.12677/SA.2019.81010
参考文献
- 1. 辛杰. 房地产业与国民经济协调发展研究[J]. 中国建设信息化, 2017(11): 76-78.
- 2. 张慧. 浅析中国房地产与国民经济[J]. 全国流通经济, 2014(7): 29-29.
- 3. 王国军, 刘水杏. 房地产业对相关产业的带动效应研究[J]. 经济研究, 2004(8): 38-47.
- 4. 何志华. 房地产相关行业的联动性及楼市调控的财富效应[C]//第八届(2013)中国管理学年会——金融分会场论文集, 2013.
- 5. 阎秋序. 房地产业与区域经济发展的关系探析[J]. 中国商论, 2015(26): 113-115.
- 6. 顾莹, 夏乐天. 加权马尔可夫链在房价预测中的应用[J]. 重庆理工大学学报, 2013, 27(8): 125-130.
- 7. 江跃勇. 成都市房价预测的一个数学模型[J]. 科技信息(学术研究), 2007(16): 392-396.
- 8. 王昱博, 李晖. 基于马氏链模型的武汉房价预测[J]. 经营管理者, 2013(12): 185-185.
- 9. 刘娜娜, 李雨洁, 唐宇, 邱益聪. 基于网络搜索词搜索量的房价预测[J]. 商, 2016(25): 294-295.
- 10. 温鲜, 霍海峰, 黄秋和. 基于多项式回归模型的柳州市房产价格预测[J]. 市场研究, 2013(8): 53-54.
- 11. 李东月. 房价预测模型的比较研究[J]. 工业技术经济, 2006, 25(9): 65-67.
- 12. 张玉芬. 马尔可夫性及其检验方法研究[J]. 价值工程, 2012, 31(2): 312-313.
