Statistics and Application
Vol.
08
No.
04
(
2019
), Article ID:
31706
,
11
pages
10.12677/SA.2019.84075
Research on College Students’ Concern about the 19th National People’s Congress
—Based on Some Universities in Nanjing City, Jiangsu Province
Yan He, Yang Li, Shan Rong, Conghui Zhang
Nanjing Audit University, Nanjing Jiangsu

Received: Jul. 25th, 2019; accepted: Aug. 7th, 2019; published: Aug. 14th, 2019

ABSTRACT
The 19th National Congress of the Communist Party of China is an important meeting that has attracted much attention at home and abroad. College students are the future of a country, and contemporary college students' attention to the 19th National People’s Congress is a reflection of students’ political accomplishments. Analyzing the influence factors of contemporary college students on the attention of the 19th National People’s Congress is conducive to the understanding of the political literacy of students by society and schools. It is beneficial to draw a feasible solution for improving students’ attention to the 19th National People’s Congress. In this paper, questionnaire data are systematically analyzed by SPSS through regression and then the proposed factors in affecting attention of the 19th National People’s Congress are evaluated.
Keywords:The 19th National People’s Congress, Questionnaire, Regression Analysis
当代大学生对党的十九大关注度 影响因素分析
——基于南京部分高校调查数据
贺研,李杨,荣珊,张聪慧
南京审计大学,江苏 南京
收稿日期:2019


摘 要
党的十九大是备受国内外关注的一次重要会议,大学生是祖国的未来,当代大学生对十九大关注度是学生政治素养的一种体现,分析当代大学生对十九大关注度的影响因素有利于社会、学校对当代学生政治素养的了解,有利于得出可行性方法提高学生对十九大的关注度。本文从十九大出发,通过分析问卷数据,利用SPSS统计软件进行回归分析,最后找出影响当代大学生对十九大关注度的因素。
关键词 :十九大关注度,问卷调查,回归分析

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 问题提出
自2017年党的十九大召开以来,青年一代的发展得到了社会的高度的关注。习近平总书记在十九大报告中提到:“青年兴则国家兴,青年强则国家强” [1] 。大学生作为青年群体中的优秀代表,是实现中国奋斗目标的重要社会群体。同时,当前国内全面深化改革,国际格局进入深刻变革时期,政治教育成为高校教育重要的组成部分,也是提高学生政治素养的主要渠道。当代大学生对时政的关注度可以从一定程度上反应政治素养,了解当前影响政治关注度的因素可以为教育工作者改善其政治教育方式方法提供重要依据,也可以让社会了解到当代大学生的时政关注度现状 [2] 。
党的十九大的召开,是备受瞩目的国际大事,更是在中国特色社会主义发展道路上的一次重要会议。此次会议关系着我国事业的发展,关系着我国社会的建设,关系着我国最广大人民的利益。我国人民对十九大的关注度也可以体现其意义之重大,影响之深远。如前所述,当代大学生作为国家的优秀群体,更应该会关注十九大,为探究当代大学生对十九大的关注度的影响因素,从2017年12月开始,本文通过开展大创项目,以十九大为出发点,以当代大学生为中心,展开了一系列调查分析工作。
同时,通过调查近期已有的研究报告并分析相似的对政治关注度或对党的十八大关注度的调查,可以得出相关调查往往只在一个学校进行或者没有深入分析其影响因素。李婷(2016)的研究以广州某“211”大学为调查对象分析出部分与大学生时事政治关注度有显著相关关系的因素,但是所调查的样本数据过于单一,属于同一院校 [3] 。何冬梅(2013)的研究属于描述统计,提供了青岛某高校学生群体回答有关十八大以及政治时事的问题的正确率的数据,但是没有进一步利用统计软件对样本数据进行相关性以及回归分析 [2] 。因此,为了进行更深入的研究,本文对南京地区三所不同类型高校(南京审计大学、南京工业大学、南京大学)进行调查,研究南京地区在校大学生的十九大关注的影响因素。同时,之前的调查报告中在对调查问卷的设计上偏向于让调查者为自己评估其政治关注度,于是产生疑问:是否会存在评估偏差或心理因素的影响?因此,本次问卷调查分为两部分:被调查者自我评估十九大关注度以及实测结果(通过回答十九大的相关问题测评出相对客观的分类结果),并将二者分别进行影响因素回归,以求得出更具有说服力的调查结果。
2. 研究设计与假设
2.1. 数据与样本
本次研究基于南京地区的三所高校进行十九大关注度影响因素的调查,目的在于探究某些变量对十九大关注度的影响情况。本调查关注的对象是江苏省内三所高校(南京审计大学、南京工业大学与南京大学学生)的学生,该调查对象的总体是三所高校的所有在校生的集合。理论上,目标总体应与抽样总体保持一致 [4] ,但实际上,受各种因素的影响,不能完全获得每一位在校生的调查数据。于是本文采用抽样的方式,根据样本提供的信息推断总体的特征。
本次调查采用不重复抽样的抽样方法,以分层随机抽样为组织方式进行问卷调查。在进行参数估计前,应先确定一个适当的样本量。由于本研究将分别调查大学生对十九大关注度的自我评估结果和客观测试得出的实测结果,所以选取的样本量应大于两种情况下所计算出的理论样本量的值。研究首先进行了一次预调查,在查阅相关文献之后,做出如下假设:
假设1:对于自我评估(关注占样本总体的比例),可接受的估计误差(E)为5%;
假设2:对于客观测试(实测结果),可接受的估计误差(E)为0.1分;
假设3:对于客观测试(实测结果),用经调整后的相似样本 [3] 的样本标准差σ = 0.402代替总体标准差;
假设4:本调查将置信水平1 − α定为99%。
自我评估方面样本量的确定用估计总体比例时样本量,即
其中 为需抽取的样本量(不重复抽样情况下), 为在置信水平为1 − α下的统计量的值, 为关注样本所占比例,E为希望达到的估计误差, 代表在重复抽样下的样本量的值,N为三所高校本科生的总人数(截止2018年,三所高校本科生人数约为五万三千名)。
客观测试方面样本量的确定用估计总体均值时样本量,即
其中 为需抽取的样本量(不重复抽样情况下), 为在置信水平为1 − α下的统计量的值,σ为总体标准差,E为希望达到的估计误差, 代表在重复抽样下的样本量的值,N为三所高校本科生的总人数(截止2018年,三所高校本科生人数约为五万三千名)。
本文所用数据来自于研究小组2018年2月到12月的调查数据。该调查采用分层抽样的方法,以学校为单位进行随机抽样,调查对象覆盖南京审计大学、南京工业大学和南京大学三所南京高校,具有较强的代表性。由于互联网问卷有不确定因素,在清洗了重要变量上不完整的问卷与系统错误问卷之后,最终有670个样本(大于上文所计算出的至少抽取658个样本)进入分析模型。
2.2. 分析方法与步骤
如前所述,问卷调查分为两部分,分别为自我评估的十九大关注度分类结果和依据回答客观问题正确率得出的分类结果(以下简称实测结果),本文将分别对这两个分类结果进行检验。其中自我评估由调查对象自己选择关注的程度,用“您认为自己是否关注十九大”进行提问,答案项分为“0:关注”和“1:不关注”。在实测结果的十九大关注度的部分中设置了与十九大相关的五道测评题,通过答对题目个数将被调查者分为五类:① 关注度低、② 关注度较低、③ 关注度适中、④ 关注度较高、⑤ 关注度高五类。研究自变量为多个因素:学校、性别、年级、专业、政治面貌。自变量的值在调查问卷中分别设置问题进行统计收集。
之后采用SPSS软件对数据进行相关的统计学处理,用卡方检验、logistic回归进行分析,具体步骤如下:
1) 自我评估结果分析:首先,将自我评估分类结果与待检验因素进行卡方检验,检测二者是否独立。其次,采用向后法–似然比检验(LR)筛选变量以检验变量是否真实独立,进行二分类logistic回归确定各因素的影响程度和方向。最后,分析回归结果。
2) 客观实测结果分析:首先,将实测结果与待检验因素进行卡方检验,检测二者是否独立。其次,对待检验因素和分类结果进行平行线检验,然后进行有序多分类logistic回归确定各因素的影响程度和方向。最后,分析回归结果。
3) 比较二者结果差异进行综合分析,得出结论。
为进行卡方检验所作假设如下(结果代指自我评估结果或实测结果):
H0:该因素与分类结果独立;H1:该因素与分类结果不独立。
基于卡方检验所得出的结果,对剩余未排除因素进行logistic回归检验,因作出如下假设:
H0:该因素对十九大关注度有影响;H1:该因素对十九大关注度没有影响。
3. 实证分析
3.1. 自我评估结果分析
1) 自我评估的结果分布
如表1所示,自我评估结果分为:① 关注、② 不关注度两类。
Table 1. Self-assessment results distribution
表1. 自我评估的结果分布
2) 自我评估结果与各因素的卡方检验
Table 2. Chi-square test of interaction between self-assessment and school
表2. 自我评估与学校交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为99.00。
Table 3. Chi-square test of interaction between self-assessment and gender
表3. 自我评估与性别交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为136.97;b. 仅针对2 × 2表进行计算。
Table 4. Chi-square test of interaction between self-assessment and grade
表4. 自我评估与年级(大一、大二 = 低年级,大三、大四 = 高年级)交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为 93.24;b. 仅针对2 × 2表进行计算。
Table 5. Chi-square test of interaction between self-assessment and political appearance
表5. 自我评估与政治面貌交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为12.50。
Table 6. Chi-square test of interaction between self-assessment and major
表6. 自我评估与专业交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为 8.71;b. 8个单元格(50.0%)的期望计数小于5,最小期望计数为1.83;c. 1个单元格(6.3%)的期望计数小于5,最小期望计数为 4.98;d. 6个单元格(42.9%)的期望计数小于5,最小期望计数为1.27。注:剔除了被调查人数较少的专业,避免对卡方检验造成影响。
由表2~6可知,通过卡方检验对学校、性别、年级、政治面貌和专业与自我评估十九大关注度进行分析,对应统计量的p值分别为0.042、0.086、0.160、0.000和0.048。从上述检验中可以得出,学校、政治面貌与自我评估结果进行检验得出的p值小于0.05,说明二者是不独立的,也就是说这些因素会对自我评估造成影响。而性别、年级这两个因素与自我评估进行检验得出的p值大于0.05,说明这两个变量没有拒绝原假设,但为了更为准确仍凭经验保留这两个变量进行logistic回归以进一步确认结果。专业因素对应的卡方检验虽然总体上表现出与分类结果不独立,但由于专业分布与学校有很大关系,在每个学校分层检验中可以明显看出专业与十九大关注度卡方检验的p值很大,所以实际专业与十九大关注度分类结果二者独立,因此在接下来的检验中并不考虑专业这一因素。
3) 二分类logistic回归
Table 7. Variables screened by backward method-likelihood ratio test
表7. 向后法–似然比检验(LR)筛选出来的变量
a. 在步骤1输入的变量:学校,性别,年级,政治面貌。
该步骤中,记关注为0,不关注为1。从表7的分析结果中可以看出,在进行向后法进行筛选变量后,年级这个变量被筛选排外(验证了步骤1中年级的卡方检验),而学校、性别、政治面貌作为影响自我评估十九大关注度的变量通过筛选,说明学校、性别、政治面貌作为影响因素质量较高。
对学校、性别、政治面貌进一步分析,可以得出如下结论:在自我评估的结果中,相对于南京审计大学的学生,南京工业大学和南京大学两所学校的学生自我评估对于十九大关注度趋向于不关注的可能性更高,举例来说,南京工业大学的学生认为自我不关注十九大的可能性是南京审计大学的学生的1.5倍;对于女性而言,男性明显更倾向于关注十九大,男性自我评估为关注十九大的可能性是女性的两倍;政治面貌属于显著影响因素,党员和入党积极分子的关注程度显著的(OR < 0.5,说明政治面貌是重要的影响因素)高于团员和群众,党员自我评估关注十九大的可能性是群众的十五倍。
以上是仅通过自我评估得出的结果,但是其中包含了很多心理因素,还需通过实测结果来进行对比分析。
3.2. 实测结果分析
1) 实测结果的分布情况
被调查者通过问题回答正确率情况被分为:① 关注度低、② 关注度较低、③ 关注度适中、④ 关注度较高、⑤ 关注度高五类。如图1可以看出分类情况属于正态分布。
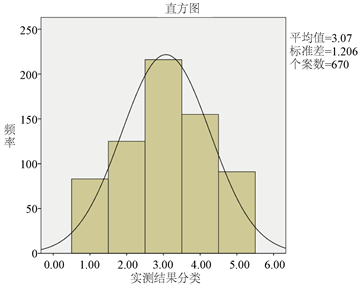
Figure 1. Distribution of testing results of the 19th national congress
图1. 十九大关注度实测结果分布情况(问题答对情况)
2) 实测结果分类与各因素的卡方检验
Table 8. Chi-square test of interaction between testing results and school
表8. 实测结果分类与学校交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为25.52。
Table 9. Chi-square test of interaction between testing results and gender
表9. 实测结果分类与性别交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为35.31。
Table 10. Chi-square test of interaction between testing results and grade
表10. 实测结果分类与年级交互效应的卡方检验
a. 0个单元格(0.0%)的期望计数小于5,最小期望计数为6.07。
Table 11. Chi-square test of interaction between testing results and political appearance
表11. 实测结果分类与政治面貌交互效应的卡方检验
a. 5个单元格(25.0%)的期望计数小于5,最小期望计数为3.22。
Table 12. Chi-square test of interaction between testing results and major
表12. 实测结果分类与专业交互效应的卡方检验
a. 11个单元格(27.5%)的期望计数小于5,最小期望计数为2.20;b. 33个单元格(82.5%)的期望计数小于5,最小期望计数为0.26;c. 23个单元格(57.5%)的期望计数小于5,最小期望计数为 1.15;d. 21个单元格(60.0%)的期望计数小于5,最小期望计数为0.25。注:剔除了被调查人数较少的专业,避免对卡方检验造成影响。
由表8~12可知,将学校、性别、年级、政治面貌和专业与实测结果分类进行卡方检验,他们统计量的渐近显著性值分别为0.000、0.291、0.734、0.000和0.000。从上述检验中可以得出,学校和政治面貌与实测结果是不独立的,也就是说这些因素会对实测结果造成影响,而性别、年级对于实测结果是独立的,从分层卡方检验结果看来,专业和实测结果是独立的,所以同样在这里排除专业这一影响因素。但是对于年级和性别,为了与之前进行对比,仍保留该因素,然后通过有序多分类logistic回归确定各因素的影响程度和方向。
3) 有序多分类logistic回归
在通过spss软件得出回归系数B,计算出OR值(EXP(B))。根据表13结果显示可以得出如下结论:随着学校变化,由南京审计大学转变为南京大学再到南京工业大学,关注度变高的可能性越来越低,即关注度向低的方向靠近,南京大学的学生处于十九大关注度相对高的可能性是南京审计大学的学生的1/2倍,南京工业大学的学生处于十九大关注度相对高的可能性是南京审计大学的学生的1/3倍,换言之,则是南京大学和南京工业大学的学生十九大关注度更低;在性别方面看来,男女同学在十九大关注度上的差异并不大,对应的p值没有经过显著性检验(验证了前面的实测结果分类与性别交互效应的卡方检验未通过);在年级方面看来,各个年级的十九大关注度无较大差异,对应的p值同样没有通过显著性检验(验证了实测结果分类与年级交互效应的卡方检验未通过);在政治面貌方面,中共党员和预备党员处于十九大关注程度高的可能性明显(OR > 2)高于共青团员和群众。政治面貌为中共党员的同学处于十九大关注度高类别的可能性是政治面貌为群众的7倍。
Table 13. Ordered multi-class logistic regression of testing results
表13. 实测结果的有序多分类logistic回归
a. 此参数冗余,因此设置为零。
3.3. 对比分析
上述分析的两次回归的结论在学校、政治面貌方面具有一致性,而在性别方面有差别,对此,本文对异同进行如下总结。
相同之处:南京工业大学和南京大学的同学在自我评估和问卷回答上处于十九大关注度低的可能性更高,原因可能与不同学校的思想政治教育有关。在政治面貌方面,两次回归结果一致,都表明了中共党员和预备党员的十九大关注度更高,这说明了中共党员和预备党员对学习十九大的主动和积极态度。在年级这个方面,两次回归的结果都没有通过显著性检验,说明年级并非十九大关注度的主要影响因素。
不同之处:自我评估的回归中性别因素通过了显著性检验,说明对结果有影响,但是在分析实测结果的回归结果中,性别因素没有通过检验,说明男性可能在心理上更倾向于认为自己关注十九大,但实际上男性与女性并没有显著区别。
4. 结论与讨论
本文研究了学校、政治面貌对于大学生十九大关注度的确产生了影响,对今后学校在引导大学生关注政治有一定的借鉴意义:“促使学生熟悉政治,使当代大学生具有在社会与国家生活中进行良好理解与判断所必需的知识与技能”,这是高校开设思想政治类课程的出发点 [5] ,偏理工科类的学校应该对时事政治教育类的课程、活动更加重视,让学生全面发展。偏文科类的学校在政治教育方面较其他类学校做得更好,可以为其他学校提供借鉴。此外,校方应有针对性的“因类施教”,引导大学生关心政治,还可以结合十九大政策导向,帮助大学生对未来做职业规划,并且可以通过开展丰富多彩的实践活动帮助大学生了解社会现实,培养主人翁责任感,增强爱国主义意识,从根本上培养大学生关注政治 [6] 。在另一方面,党员和预备党员应起到模范带头的作用,带领普通同学共同进步,学习党的知识,提高思想觉悟,带动身边的同学关注政治、关心国家大事,在提高全体学生思想政治素质方面起到积极作用 [7] ,学校也应做到引导党员和预备党员发挥带头作用。
基金项目
本文系南京审计大学2018年度大学生创新创业训练计划项目(项目编号:201811287009Z)的成果。
文章引用
贺 研,李 杨,荣 珊,张聪慧. 当代大学生对党的十九大关注度影响因素分析——基于南京部分高校调查数据
Research on College Students’ Concern about the 19thNational People’s Congress—Based on Some Universities in Nanjing City, Jiangsu Province[J]. 统计学与应用, 2019, 08(04): 664-674. https://doi.org/10.12677/SA.2019.84075
参考文献
- 1. 习近平. 决胜全面建成小康社会夺取新时代中国特色社会主义伟大胜利[N]. 人民日报, 2017-10-28(001).
- 2. 何冬梅. 大学生对党的十八大关注度调查分析与研究——以青岛某高校中外合作办学理工类专业为例[J]. 学理论, 2013(23): 195-196.
- 3. 李婷. 大学生时事政治关注状况的调查研究[J]. 广东青年职业学院学报, 2016, 30(40): 28-32.
- 4. 杨光辉. 对多目标抽样的再认识[J]. 统计与决策, 2013(8): 32-35.
- 5. 唐湘宁. 大学生政治参与的意义[J]. 辽宁行政学院学报, 2006, 8(12): 25-26.
- 6. 张甲田. 思想政治教育视域下大学生对社会热点问题的关注及引导研究[J]. 当代教育实践与教学研究, 2017(5): 264-265.
- 7. 陶祚. 大学生党员发挥先锋模范作用的实现途径探究[J]. 品牌研究, 2018, 18(6): 219-220.
