Statistics and Application
Vol.
10
No.
02
(
2021
), Article ID:
41863
,
6
pages
10.12677/SA.2021.102027
基于水平镜像算法的改进Box-Cox变换
陈鸿
云南师范大学数学学院,云南 昆明

收稿日期:2021年3月31日;录用日期:2021年4月15日;发布日期:2021年4月26日

摘要
基于服从负偏态分布数据的一种水平镜像算法,本文提出一种改进Box-Cox变换——镜像Box-Cox变换,并进行数值实验,实验结果显示,与传统的Box-Cox变换相比较,镜像Box-Cox变换在处理正偏态分布数据的效果上与传统Box-Cox变换处理效果相同的基础上,其处理负偏态分布数据的效果要优于传统Box-Cox变换。再进行模拟回归模型实验,实验结果表明,经过镜像Box-Cox变换的数据建立的回归模型的拟合和预测效果有所提高,且效果优于使用传统Box-Cox变换后的数据。
关键词
Box-Cox变换,水平镜像算法,极大似然估计法
Improved Box Cox Transform Based on Horizontal Mirror Algorithm
Hong Chen
School of Mathematics, Yunnan Normal University, Kunming Yunnan

Received: Mar. 31st, 2021; accepted: Apr. 15th, 2021; published: Apr. 26th, 2021

ABSTRACT
Based on a horizontal mirror algorithm for data with negative skew distribution, this paper proposes an improved Box-Cox transform: mirror Box-Cox transform, and carries out numerical experiments. The experimental results show that, compared with the traditional Box-Cox transform, mirror Box-Cox transform can process negative skewness on the basis of the same effect as the traditional Box-Cox transform. The effect of distributed data is better than that of traditional Box-Cox transform. Then the simulated regression model experiment is carried out. The experimental results show that the fitting and prediction effect of the regression model established by the mirror Box-Cox transformation data is improved, and the effect is better than the data after using the traditional Box-Cox transformation.
Keywords:Box-Cox Transform, Horizontal Mirror Algorithm, Maximum Likelihood Estimation Method

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 研究背景
现实中,我们会遇到的数据纷繁复杂,不同的数据根据我们所做的假设的不同,需要进行不同的变换,以便我们能够在已有理论上对其进行分析。例如:股票收益率等数据的特殊性,不可观测的误差可能是和预测变量相关的,但其不服从正态分布,于是给线性回归的最小二乘估计系数的结果带来误差,为了满足线性回归的四个假设条件而又不丢失信息,有时需要对数据进行处理变换;又例如方差分析需要试验误差具有独立性、无偏性、方差齐性和正态性的条件,若不满足这些条件就需要对数据进行处理 [1]。
Box-Cox变换是George Box和David Cox在1964年提出的一种参数化广义幂变换方法 [2],其主要特点是引入一个参数 ,通过数据本身估计该参数 ,从而确定应采取数据变换形式 [3]。常用于稳定方差、减少数据在统计建模中的非正态性和增强关联性度量的有效性。
基于正偏和负偏的数据互为镜像关系,本文提出的镜像Box-Cox变换,提高偏态分布数据正态化效果,且便于运算,并进行数值实验以验证该结论。
1.2. 正态性检验及回归模型评价指标说明
1) Shapiro-Wilk检验 [4] (W检验)
W检验是用来检验数据是否符合正态分布的。可计算得到一个相关系数,它越接近1就越表明数据和正态分布拟合得越好。且W检验还会给出一个P值,若P值大于0.05,就无法拒绝其符合正态分布。若统计量W值接近1,但P值小于0.05,我们仍然拒绝其符合正态分布。W检验计算公式为:
其中, 为样本的次序统计量, 为一个待估常量。
2) MAPE [5] (Mean Absolute Percentage Error,平均绝对百分比误差)
MAPE常用于描述准确度,它是一个百分比值,因此比其他统计量更容易理解。MAPE的值越小,说明预测模型拥有更好的精确度。其数学表达式为:
2. Box-Cox变换
假设样本里一共有n个数据点,分别是: ,我们把变换后新的数据点记为:
当 时,Box-Cox变换是对原始数据做如下变换:
(1)
当存在 时,Box-Cox变换是对原始数据进行如下变换:
(2)
是一个待定变换参数,对不同的 ,所做的变换自然就不同,所以这是一个变换族。我们将(1)式称为Box-Cox变换的基本公式;将(2)式称为Box-Cox变换的扩展公式。
3. 镜像Box-Cox变换
众所周知,在面对偏态分布数据时,我们需要使其变换为正态分布,要在保持数据大小次序不变的同时,减小数据之间的距离。对于处理正偏态分布的数据就需要一类增长率单调递减的函数,例如对数函数、平方根函数等等。而根据Box-Cox变换公式:
要使变换函数增长率单调递减,就需要变换的二阶导数小于0,即:
故Box-Cox变换在处理正偏态分布数据时,待定变换参数 ,同理可得,其在处理负偏态分布数据时,待定变换参数 。
所以,Box-Cox变换在处理正偏态分布数据时,相较于其处理负偏态分布数据时,除了幂函数,还多了对数变换,且变换参数的取值范围较小,易于求解。
理论介绍
,镜像Box-Cox变换是对原始数据做如下变换:
(3)
若原始数据服从正偏态分布,且 ,则: , ;若原始数据服从正偏态分布,且 ,则: , ;若原始数据服从负偏态分布,则: , 其中, 表示原始数据取绝对值后,数据中的最大数。
无论选择传统的Box-Cox变换还是镜像Box-Cox变换,最关键的问题在于怎样选定一个最优的 ,使得变换后的样本(及总体)正态性最好 [6]。求解最优参数 ,我们可以采用极大似然估计法和Bayes方法 [6] [7]。
4. 数值实验
我们将分三种情况进行数值实验:1) 数据全为正数,2) 数据全为负数,3) 数据有一部分正数和一部分负数。
本节使用Python软件随机生成上述三种情况的负偏态分布 [8] 数据,之后将此类数据分别使用传统的Box-Cox变换和本文提出的镜像Box-Cox变换进行处理,对变换后的数据进行偏度、峰度 [9] 和Shapiro-Wilk [10] 检验,并画出数据的频率直方图和P-P图,据此可以比较两种变换的效果。
4.1. 符号说明
本节将实验中处理的不同数据使用不同的符号表示,便于之后的实验结果的描述,符号说明如表1所示。
Table 1. Symbol description
表1. 符号说明
4.2. 实验结果
4.2.1. 数据正态性检验图示结果
图1从左到右分别表示的是І−型、П−型、Ш−型、TІ−型、TП−型、TШ−型、MІ−型、MП−型和MШ−型数据的直方图和P-P图。从图中可以看出经过镜像Box-Cox变换后的数据更加接近正态分布。
4.2.2. 数据正态性假设检验结果
从表2中可以看出无论是І−型、П−型还是Ш−型数据,经过镜像Box-Cox变换后的数据在偏度、峰度和W值的表现均比传统Box-Cox变换后的数据更加接近正态分布。
5. 回归模型模拟
5.1. 实验分析
生成一组服从负偏态分布的回归因变量,数据中即包含正数、也包含负数,计算原始数据的偏度、峰度,并进行Shapiro-Wilk检验,之后对原始数据建立回归模型,进行预测并计算MAPE;再使用传统Box-Cox变换及镜像Box-Cox变换对原始数据进行处理,计算经过变换后的数据的偏度、峰度,并进行Shapiro-Wilk检验,之后使用处理后的数据建立回归模型,进行预测并计算MAPE。
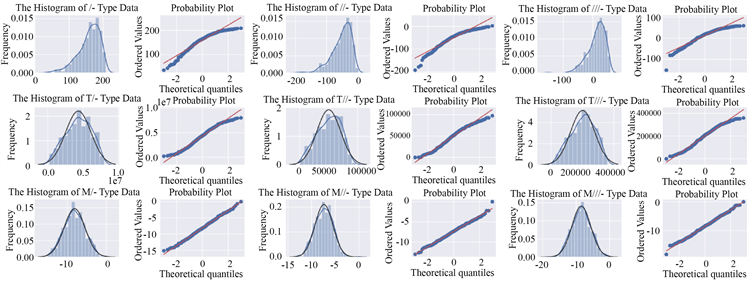
Figure 1. The histogram and P-P plot of three type data
图1. 三类数据的频率直方图和P-P图
Table 2. Data normality test results and optimal parameters ( λ )
表2. 数据正态性检验结果及最优参数( λ )
5.2. 实验结果
从表3可以得到经过镜像Box-Cox变换后的数据更接近正态分布,并且其预测值与实际值的平均绝对百分比误差(RMSE)为2.802%,远小于传统Box-Cox变换后的数据的70.77%。
Table 3. Data normality test results and model fitting effect evaluation
表3. 数据正态性检验结果及模型拟合效果评价
6. 结语
通过数值实验,我们发现无论何种类型(全为正数、全为负数和部分正数、部分负数)的负偏态分布数据经过镜像Box-Cox变换后,数据基本服从正态分布,且效果要优于使用传统Box-Cox变换。
进行模拟回归模型实验结果表明,使用传统Box-Cox变换后的数据建立的回归模型,进行预测后其RMSE为70.77%;使用镜像Box-Cox变换后的数据建立的回归模型,进行预测后其RMSE为2.802%,经过镜像Box-Cox变换的数据建立的回归模型的拟合和预测效果有所提高,且效果优于使用传统Box-Cox变换后的数据。
本文提出的镜像Box-Cox变换通过计算机易于实现,效果相较传统Box-Cox变换有所提高,可以作为处理非正态数据的一种可靠的方法。
文章引用
陈 鸿. 基于水平镜像算法的改进Box-Cox变换
Improved Box Cox Transform Based on Horizontal Mirror Algorithm[J]. 统计学与应用, 2021, 10(02): 278-283. https://doi.org/10.12677/SA.2021.102027
参考文献
- 1. 张彦玲. 处理非正态数据[J]. 中国质量, 2002(8): 22-24.
- 2. Box, G. and Cox, D. (1964) An Analysis of Transformations (with Discussion). Journal of the Royal Statistical Society, Series B, 26, 211-252.
https://doi.org/10.1111/j.2517-6161.1964.tb00553.x - 3. 王松桂, 陈敏, 陈立萍. 线性统计模型——线性回归与方差分析[M]. 北京: 高等教育出版社, 1999: 52-55.
- 4. Shapiro, S.S. and Wilk, M.B. (1965) An Analysis of Variance Test for Normality (Complete Samples). Biometrika, 52, 591-611.
https://doi.org/10.1093/biomet/52.3-4.591 - 5. Hyndman, R.J. and Koehler, A.B. (2006) Another Look at Measures of Forecast Accuracy. International Journal of Forecasting, 22, 679-688.
https://doi.org/10.1016/j.ijforecast.2006.03.001 - 6. 钟登华, 刘豹. Box-Cox变换模型参数估计方法研究[J]. 系统工程学报, 1993, 8(2): 40-46.
- 7. 胡宏昌, 樊献花, 等. 广义Box-Cox变换[J]. 周口师范学院学报, 2006, 23(5): 17-18.
- 8. Azzalini, A. and Capitanio, A. (1999) Statistical Applications of the Multivariate Skew-Normal Distribution. Journal of the Royal Statistical Society: Series B, 61, 579-602.
https://doi.org/10.1111/1467-9868.00194 - 9. 茆诗松, 周纪芗. 概率论与数理统计[M]. 北京: 中国统计出版社, 2013: 260-262, 420-422.
- 10. Rigby, R.A. and Stasinopoulos, D.M. (2010) Smooth Centile Curves for Skew and Kurtotic Data Modelled Using the Box-Cox Power Exponential Distribution. Stats in Medicine, 23, 3053-3076.
https://doi.org/10.1002/sim.1861
