Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19031,5
pages
10.12677/AAM.2016.54075
The Asymptotic Expansion Related to the Similar Constant B of Glaisher-Kinkelin Constant A
Chaomin Tang*, Hongmei Liu, Yunxiao Shi, Guiqing Shi
School of Science, Dalian Nationalities University, Dalian Liaoning

Received: Nov. 2nd, 2016; accepted: Nov. 18th, 2016; published: Nov. 24th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, by the Bernoulli numbers and the exponential complete Bell polynomials, we establish one general asymptotic expansion related to the similar constant B of Glaisher-Kinkelin constant A and the function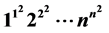 .
.
Keywords:Glaisher-Kinkelin Constant A, Similar Constant B, Asymptotic Expansion

关于Glaisher-Kinkelin常数A的类似常数B的 渐近展开
唐超敏*,刘红梅,史云霄,石桂庆
大连民族大学理学院,辽宁 大连

收稿日期:2016年11月2日;录用日期:2016年11月18日;发布日期:2016年11月24日

摘 要
在本文中,通过Bernoulli数和指数型完全Bell多项式,我们建立了关于Glaisher-Kinkelin常数A的类似常数B和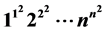 的渐近展开式。
的渐近展开式。
关键词 :Glaisher-Kinkelin常数A,类似常数B,渐近展开

1. 引言
Glaisher-Kinkelin常数 被定义为:
被定义为:
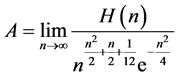 ,(1.1)
,(1.1)
其中,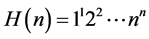 为超阶乘函数。最近,根据Euler-Maclaurin公式,Chen [1] 给出了下列关于超阶乘函数和Glaisher-Kinkelin常数
为超阶乘函数。最近,根据Euler-Maclaurin公式,Chen [1] 给出了下列关于超阶乘函数和Glaisher-Kinkelin常数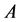 的渐近展开:
的渐近展开:
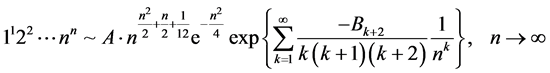 , (1.2)
, (1.2)
其中, 为Bernoulli数。
为Bernoulli数。
在式(1.2)的基础上,Wang and Liu [2] 对超阶乘函数和Glaisher-Kinkelin常数推导出以下一般渐近展开:
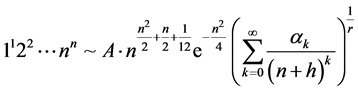 .(1.3)
.(1.3)
最近,我们发现,Chen [1] 还建立了以下关于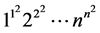 和常数
和常数 的渐近展开:
的渐近展开:
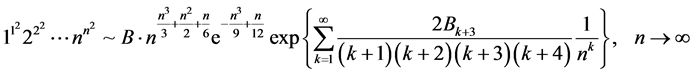 (1.4)
(1.4)
其中, 为Glaisher-Kinkelin常数
为Glaisher-Kinkelin常数 的类似常数。
的类似常数。
以上知识给了我们一个启发,我们希望通过Bernoulli数和指数型完全贝尔多项式去推导出关于Glaisher-Kinkelin常数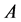 的类似常数
的类似常数 和
和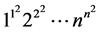 的渐近展开:
的渐近展开:
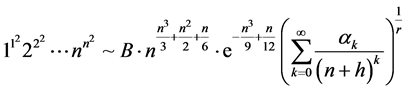 .(1.5)
.(1.5)
为了得到这个渐近展开式,我们需要下列指数型完全Bell多项式的相关知识。指数型完全Bell多项式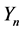 被定义为(见 [3] , Section 3.3):
被定义为(见 [3] , Section 3.3):
 . (1.6)
. (1.6)
它的具体表达式为:
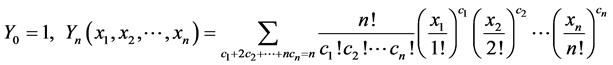 . (1.7)
. (1.7)
另外,根据 [4] , p.36, Equation (44)和 [5] , Theorem 1可以知道多项式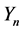 满足递归式:
满足递归式:
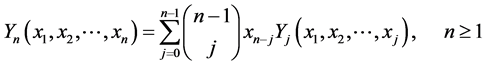 . (1.8)
. (1.8)
2. 定理及证明
2.1. 定理
令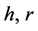 为实数,
为实数,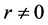 ,并定义
,并定义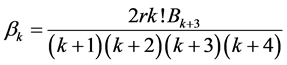 ,则我们有下列关于
,则我们有下列关于 和常数
和常数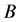 的渐近展开:
的渐近展开:
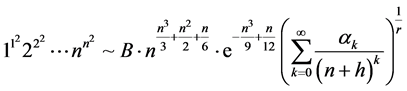 ,
,
其中,当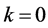 时,
时,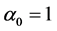 ;当
;当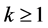 时,
时,
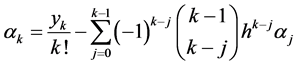 , (2.1)
, (2.1)
在式(2.1.1)中,当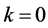 时,
时, ;当
;当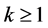 时,
时,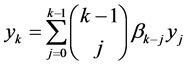 .
.
2.2. 证明
令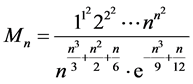 ,由(1.6)以及
,由(1.6)以及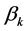 的定义,我们可以将式(1.4)改写为:
的定义,我们可以将式(1.4)改写为:
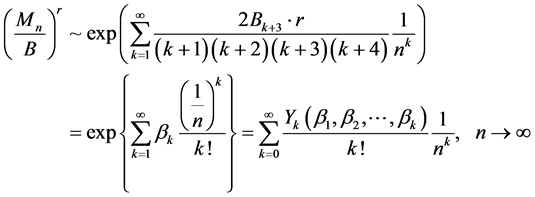
另外,将 展开为关于
展开为关于 的幂级数:
的幂级数:
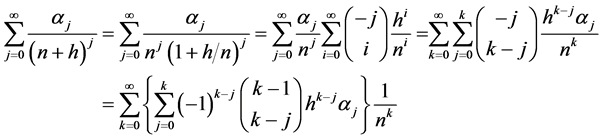 .
.
要证: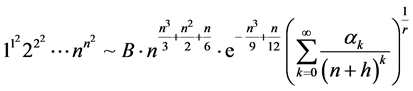 ,即要使下列等式成立:
,即要使下列等式成立:
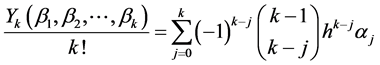 .
.
当我们定义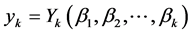 时,上式可以写成:
时,上式可以写成:
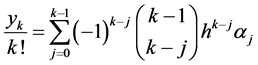 .
.
通过以上等式,我们得到一个唯一解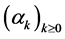 ,而且
,而且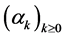 有如下递推关系:
有如下递推关系:
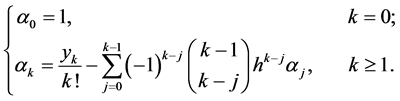
其中, 满足(1.8),定理得证。
满足(1.8),定理得证。
通过指数型完全Bell多项式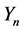 的定义(1.6)我们可以容易地计算出
的定义(1.6)我们可以容易地计算出 。下面我们列出
。下面我们列出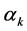 的前几项:
的前几项:
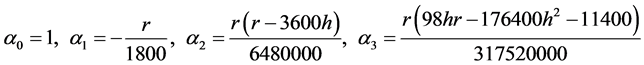 .
.
将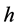 和
和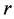 取特殊值,我们可以得到一系列有关Glaisher-Kinkelin常数
取特殊值,我们可以得到一系列有关Glaisher-Kinkelin常数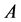 的类似常数
的类似常数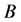 和
和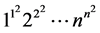 的渐近展开。下面我们举出几个例子。
的渐近展开。下面我们举出几个例子。
3. 例子
令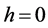 ,
,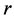 分别取1,2,3,当
分别取1,2,3,当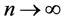 时,我们有:
时,我们有:
 ,
,
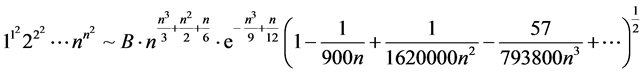 ,
,
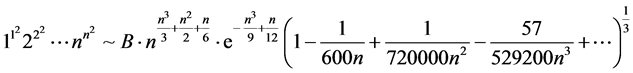 .
.
基金项目
国家自然科学基金/Natural Science Foundation of China (11501081),省级大学生创新创业训练计划项目(项目编号:S201612026050),中央高校基本科研基金(DC201502050405)。
文章引用
唐超敏,刘红梅,史云霄,石桂庆. 关于Glaisher-Kinkelin常数A的类似常数B的渐近展开
The Asymptotic Expansion Related to the Similar Constant B of Glaisher-Kinkelin Constant A[J]. 应用数学进展, 2016, 05(04): 646-650. http://dx.doi.org/10.12677/AAM.2016.54075
参考文献 (References)
- 1. Chen, C.-P. (2012) Glaisher-Kinkelin Constant. Integral Transforms and Special Functions, 23, 785-792.https:/doi.org/10.1080/10652469.2011.632501
- 2. Wang, W.P. and Liu, H.M. (2016) Asymptotic Expansions Related to Hyperfactorial Function and Glaisher-Kinkelin Constant. Applied Mathematics and Computation, 283, 153-162. https:/doi.org/10.1016/j.amc.2016.02.027
- 3. Comtet, L. (1974) Advanced Combinatorics. D. Reidel Publishing Co., Dordrecht. https:/doi.org/10.1007/978-94-010-2196-8
- 4. Riordan, J. (2002) An Introduction to Combinatorial Analysis. Dover Publications, Inc., Mineola, NY. Reprint of the 1958 Original.
- 5. Rota Bulo, S., Hancock, E.R., Aziz, F. and Pelillo, M. (2012) Efficient Computation of Ihara Coefficients Using the Bell Polynomial Recursion. Linear Algebra and Its Applications, 436, 1436-1441. https:/doi.org/10.1016/j.laa.2011.08.017
*通讯作者。