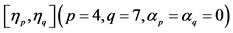Advances in Applied Mathematics
Vol.06 No.02(2017), Article ID:20025,5
pages
10.12677/AAM.2017.62021
Monophyletic Representation of Random Vector
Shuo Zhuang, Jihui Ding, Baoxin Tang
School of Civil Science and Engineering, Yangzhou University, Yangzhou Jiangsu

Received: Mar. 9th, 2017; accepted: Mar. 27th, 2017; published: Mar. 30th, 2017

ABSTRACT
Based on orthogonal function theory and Karhunen-Loeve decomposition method, monophyletic random vector is constructed to solve the reduction of random variables in stochastic structural analysis. Based on the probability theory, the approximate independence of the monophyletic random vector and the construction method of the monophyletic random vector are studied. The results show that: 1) the monophyletic random vector is independent, the accuracy is sufficient to meet the engineering requirements; 2) the monophyletic random vector is simple and repeatable. Furthermore, it provides a new method for the stochastic analysis of structures.
Keywords:Structure Stochastic Analysis, Monophyletic, Random Vector Reduction, Approximate Independence
随机向量的单源表达方法
庄硕,丁继辉,汤保新
扬州大学建筑科学与工程学院,江苏 扬州
收稿日期:2017年3月9日;录用日期:2017年3月27日;发布日期:2017年3月30日

摘 要
基于正交函数理论和Karhunen-Loève分解法,构造了一种单源随机向量,从而实现了结构随机分析中随机变量的缩减。基于概率论方面的相关理论,研究了单源随机向量的近似独立性和单源随机向量的构造方法。结果表明:1) 单源随机向量近似独立,精度满足工程要求;2) 单源随机向量构造简单。这为结构随机分析提供了一个新的手段。
关键词 :结构随机分析,单源,随机向量缩减,近似独立

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前为减少实际工程基本随机变量个数,一种可靠的方法是通过数学上的正交变换方法缩减随机变量个数。下面以随机过程的描述为例。Karhunen-Loève分解法 [1] 将随机过程分解为各分量不相关的正交函数叠加,大约需要200~600个基本随机变量。李杰等 [2] [3] 进一步研究基于标准正交基的随机过程展开法,通过随机向量的相关分解对展开系数实施正交化,基本随机变量一般为10~20个左右。汤保新 [4] [5] 对李杰等采用的不相关的基本随机变量再次采用单源随机向量(正交函数)表达,随机过程的描述仅需1个基本随机变量。
本文给出了“单源随机向量”概念的更一步解释,并探讨了单源随机向量的近似独立性和构造方法。
2. 单源随机向量的概念
“单源”是遗传学上的概念,它在模糊数学和力学领域已有借用的范例 [6] [7] 。
所谓单源随机向量 [8] (monophyletic random vector),是指以同一个随机变量为自变量的一组随机函数序列。如 ,其中,
,其中, ,
, 为唯一的随机源变量,则称
为唯一的随机源变量,则称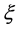 为单源随机向量。可以构造一个分量服从反正弦分布的单源随机向量,
为单源随机向量。可以构造一个分量服从反正弦分布的单源随机向量,
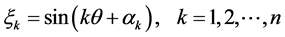 (1)
(1)
式中, 为
为 上均匀分布的唯一随机变量,
上均匀分布的唯一随机变量,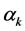 为任意确定的常量。容易推导,
为任意确定的常量。容易推导, 的概率密度函数形式同为,
的概率密度函数形式同为,
 (2)
(2)
概率分布函数为
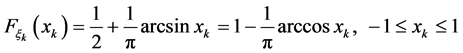 (3)
(3)
由此可见, 的各分量服从同一分布,均值
的各分量服从同一分布,均值 ,均方差
,均方差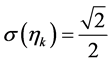 。任意两个分量之间的相关系数
。任意两个分量之间的相关系数 ,即各分量之间不相关,但并不相互独立。单源随机向量的性质将决定其应用,下一节介绍其性质的研究。
,即各分量之间不相关,但并不相互独立。单源随机向量的性质将决定其应用,下一节介绍其性质的研究。
3. 单源随机向量的近似独立性
因为随机源相同,单源随机向量的各分量之间通过唯一随机源相联系,所以各分量之间是不独立的,存在一定的相依关系。这种关系,经典概率论一般采用独立性和线性相关系数描述,但这种描述存在一定局限性 [9] 。
这里仅研究三角函数形式的单源随机向量 或
或 的近似独立性,这里
的近似独立性,这里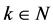 ,
, 服从
服从 上的均匀分布(以下记为
上的均匀分布(以下记为 )。
)。
1) 先考虑用联合概率分布是否等于各边缘分布的乘积来判断。
公式推导发现联合概率分布不等于各边缘分布的乘积。在严格的概率意义上, 是不相互独立的。但从数值计算结果看,
是不相互独立的。但从数值计算结果看, 与
与 很接近,见图1。误差大小跟
很接近,见图1。误差大小跟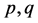 的取值有关,当
的取值有关,当 时,最大误差0.0063;当
时,最大误差0.0063;当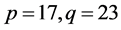 时,最大误差0.0067。由于
时,最大误差0.0067。由于 ,所以,在不太严格的概率意义上说,
,所以,在不太严格的概率意义上说,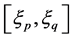 是接近相互独立的,不妨称之为近似独立。
是接近相互独立的,不妨称之为近似独立。
2) 其次考虑按统计学方法通过样本检验来判断。
这里采用二维列联表的独立性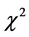 检验 [10] 。将
检验 [10] 。将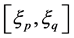 的值域离散为
的值域离散为 个区格,抽样统计每个区格的频数
个区格,抽样统计每个区格的频数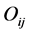 ,与每个区格的理论频数
,与每个区格的理论频数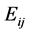 进行比较,计算统计量
进行比较,计算统计量
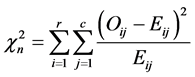 (4)
(4)
当该统计量服从自由度为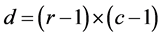 的
的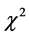 分布时,说明抽样数据相互独立。取显著水平为
分布时,说明抽样数据相互独立。取显著水平为 ,检验结果见表1。由表可见,
,检验结果见表1。由表可见, ,所以无法拒绝抽样数据的独立性。
,所以无法拒绝抽样数据的独立性。
3) 最后按高阶相关系数度量单源随机向量的近似独立性。
基于多边矩阵理论 [11] ,罗纯、王晓迪、张应山 [12] 给出了两组随机向量相互独立和相互观测独立的定义,推出了框架的正交性与随机变量的独立性等价定理。崔瑞峰、牛新军 [13] 以高阶相关系数描述随机变量之间的非线性关系,定义了两个随机变量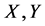 的n阶协方差矩阵,
的n阶协方差矩阵,
 ,当
,当 时,称
时,称 为n阶不相关。研究证明,对两个
为n阶不相关。研究证明,对两个
连续型随机变量,任意高阶不相关与相互独立等价。
由于协方差的计算会受到量纲的影响,这里定义两个随机变量 的n阶相关系数矩阵(无量纲),
的n阶相关系数矩阵(无量纲),
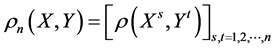 ,那么,可将高阶相关系数矩阵接近不相关矩阵
,那么,可将高阶相关系数矩阵接近不相关矩阵 的程度作为两个随机
的程度作为两个随机
变量逼近相互独立的判据。本文研究了两个随机变量的情形。由定义
 (5)
(5)
不难推导各阶相关系数。
这里以四阶相关系数( )为例。此时有
)为例。此时有 ,或
,或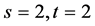 ,或
,或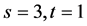 三种情形。利用对称性,仅需讨论前2种情形,结果如下:
三种情形。利用对称性,仅需讨论前2种情形,结果如下:
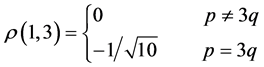 ,
,  ,
,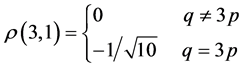 (6)
(6)
其它各阶相关系数最大值见表2。
研究发现,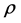 均与
均与 的取值有关。当
的取值有关。当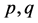 经过约简后,如果
经过约简后,如果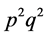 值较大,则各阶相关系数较小。可以通过适当的
值较大,则各阶相关系数较小。可以通过适当的 选值,达到一定的接近独立的程度。
选值,达到一定的接近独立的程度。
4. 任意分布单源随机向量的构造
由均匀分布单源随机向量
 (7)
(7)
可构造任意类型的概率分布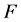 ,
,
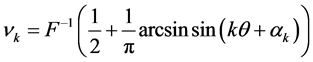 (8)
(8)
由式(7)所构造的均匀分布函数近似独立,如图2所示。
用正态分布作为媒介,通过变换,进行单源构造后,可将实际随机变量的数量减少到1个。

 (a) 边缘分布的乘积 (b) 联合概率分布
(a) 边缘分布的乘积 (b) 联合概率分布
Figure 1. Two dimensional joint probability distribution function
图1. 二维联合概率分布函数
Table 1. The independence test of two dimensional contingency table
表1. 二维列联表的独立性检验
Table 2. Higher order correlation coefficients of two random variables
表2. 两个随机变量的高阶相关系数
注: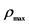 为相关系数绝对值的最大值。
为相关系数绝对值的最大值。
图2. 二维均匀分布直线网格
5. 结论
综上所述,单源随机向量 在概率论上本质是不独立的,但相当接近于独立。高阶相关系数足够小且统计检验又无法拒绝抽样数据的独立性,可以说,单源随机向量所表现的统计意义上的观测独立性达到了“以假乱真”的效果,甚或掩盖了概率意义上的不相互独立的本质。对数值模拟来说,如果单源随机向量近似独立,当抽样次数不多时亦可满足样本点的独立性要求,这为有效减少抽样次数提供了方法论上的依据,也为结构随机分析提供了新的手段。
在概率论上本质是不独立的,但相当接近于独立。高阶相关系数足够小且统计检验又无法拒绝抽样数据的独立性,可以说,单源随机向量所表现的统计意义上的观测独立性达到了“以假乱真”的效果,甚或掩盖了概率意义上的不相互独立的本质。对数值模拟来说,如果单源随机向量近似独立,当抽样次数不多时亦可满足样本点的独立性要求,这为有效减少抽样次数提供了方法论上的依据,也为结构随机分析提供了新的手段。
基金项目
国家自然科学基金资助项目(51541805)。
文章引用
庄硕,丁继辉,汤保新. 随机向量的单源表达方法
Monophyletic Representation of Random Vector[J]. 应用数学进展, 2017, 06(02): 183-187. http://dx.doi.org/10.12677/AAM.2017.62021
参考文献 (References)
- 1. Loève, M. (1977) Probability Theory. Springer-Verlag, Berlin.
- 2. 李杰, 刘章军. 基于标准正交基的随机过程展开法[J]. 同济大学学报: 自然科学版, 2006, 34(10): 1279-1283.
- 3. 刘章军, 李杰. 地震动随机过程的正交展开[J]. 同济大学学报: 自然科学版, 2008, 36(9): 1153-1159.
- 4. Tang, B.X., Cheng, K.H. and Li, Q. (2011) Simulating Stochastic Process with a Monophyletic Random Vector. Sustainable Development of Urban Environment and Building Material, Tran Tech Publications, Zurich-Durnten, 1698- 1703.
- 5. 汤保新. 随机结构的单源随机向量表达[J]. 扬州大学学报, 2011, 14(4): 64-68.
- 6. 王柏生. 单源模糊数及运算[J]. 模糊系统与数学, 1998, 12(2): 49-53.
- 7. 刘长虹, 陈虬. 单源模糊数的模糊随机有限元方程的解法[J]. 应用数学与力学, 2000, 21(11): 1147-1150.
- 8. 汤保新. 单源随机向量及其在随机分析中的应用[J]. 工程力学, 2012, 29(12): 51-55.
- 9. 严忠权. 随机变量相依关系的度量[J]. 黔南民族师范学院学报, 2008(6): 34-38.
- 10. 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 第3版. 北京: 高等教育出版社, 2001.
- 11. 张应山. 多边矩阵理论[M]. 北京: 中国统计出版社, 1993.
- 12. 罗纯, 王晓迪, 张应山. 正交性与独立性——处理复杂系统的新思维系列之三[J]. 上海应用技术学院学报: 自然科学版, 2010, 10(4): 271-277.
- 13. 崔瑞峰, 牛新军. 随机变量相互独立与不相关之间关系的推广[J]. 西安电子科技大学学报, 1999, 26(2): 262-264.




 (b)
(b) (c)
(c)