Advances in Applied Mathematics
Vol.06 No.05(2017), Article ID:21815,10
pages
10.12677/AAM.2017.65086
A Class of Improved Algorithm for Solving Interval Nonlinear Equation
Liang Qiu, Haijun Wang*, Qi Wang
School of Mathematics, China University of Mining and Technology, Xuzhou Jiangsu
*通讯作者。

Received: Aug. 6th, 2017; accepted: Aug. 20th, 2017; published: Aug. 25th, 2017

ABSTRACT
In this paper, we consider the problem of solving interval nonlinear equation with interval parameters. Dividing the initial interval by monotone segment technique, we extended the improved interval Newton algorithm proposed in [1] , and established a class of improved algorithm for solving interval nonlinear equation. Besides, some relevant theoretical results and effectiveness tests are given. Numerical examples show the new algorithm can not only solve problems that can not be solved by improved interval
Keywords:Interval Nonlinear Equation with Interval Parameters, Improved Interval Newton Algorithm, Subinterval, Interval Zero
求解区间非线性方程的一类改进算法
邱亮,王海军*,王琪
中国矿业大学数学学院,江苏 徐州

收稿日期:2017年8月6日;录用日期:2017年8月20日;发布日期:2017年8月25日

摘 要
本文研究了含区间参数的区间非线性方程的求解问题,通过单调分割技术对初始区间进行并行划分,对文献 [1] 中的拓展区间牛顿算法进行了改进,建立了一类求解区间非线性方程的新算法,给出相关的理论结果并进行数值有效性测试。数值算例表明新算法不仅可以解决拓展区间牛顿法不能解决的问题,并且大大提高了计算效率。
关键词 :含区间参数的区间非线性方程,拓展的区间牛顿算法,子区间,零解区间

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
传统的非线性方程可以表示为:
 (1)
(1)
这里 是连续可微的函数,
是连续可微的函数,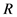 表示所有的实数。
表示所有的实数。
在众多科学领域(如:化工 [2] 、计算机图形学 [3] 、机器人科学 [4] 、控制理论 [5] 等)中,都会涉及到(1)的求解。但是,在现实问题中考虑到实验过程中实验方法、实验仪器等存在的误差、计算过程中浮点数运算出现的误差,在实际计算中我们常常需要解决的是求解含不定参数的非线性方程:
 (2)
(2)
这里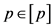 ,
,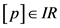 ,
, 表示所有实区间集合。下面我们给出含区间参数的区间非线性方程的定义:
表示所有实区间集合。下面我们给出含区间参数的区间非线性方程的定义:
定义1.1 是连续可微的函数,
是连续可微的函数, 是初始区间,
是初始区间, 是包含
是包含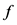 所有系数的区间向量,则含区间参数的区间非线性方程可表示为:
所有系数的区间向量,则含区间参数的区间非线性方程可表示为:
 (3)
(3)
定义1.2 ,
, 的每一个连续的零解集合构成区间方程
的每一个连续的零解集合构成区间方程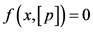 的一个零解区间,如果该零解区间只包含一个值,称其为退化的零解区间。
的一个零解区间,如果该零解区间只包含一个值,称其为退化的零解区间。
区间方程(3)的所有零解就是方程(2)所有方程零解的集合。显然区间方程(3)的解有3种情况:空区间、退化区间(区间内只包含一个值)和非退化区间。对于非退化区间来说,包含在其中的零解是无穷多的,方程(2)的系数是不断变化的,其零解也是不断变化的。但是,区间方程(3)的解区间的个数是有限的,所以我们不直接求方程(2)的零解,而求其解区间。
1966年,Moore [6] 在《Interval Analysis》一书中第一次用区间牛顿法逼近了一个简单的区间方程的零解;1992年,Hansen [7] 利用牛顿法提出了区间搜索和启发式的终止条件求解区间方程的零解;2006年,Nikas [8] 等,在理论上提出了一种边界近似的方法求解区间方程,并取得了很好的成果;2009年,Nikas [1] 等,又基于牛顿法提出了通过分离零解区间端点的方法求解区间方程。
本文基于Nikas提出的分离零解区间端点的方法,首先考虑区间函数在指定初始区间内不单调的情况下,先分割出存在零解的各个单调子区间,再逼近其零解区间的各个端点。数值算例证明该方法可在更少的迭代步下确定零解区间。
2. 拓展的区间牛顿法(EIN)
对于 ,
, ,
, 是方程的解,且
是方程的解,且 ,则传统的区间牛顿法公式为:
,则传统的区间牛顿法公式为:
 (4)
(4)
其中: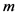 是
是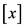 内的任意一点(通常取
内的任意一点(通常取 为
为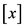 的中点),
的中点),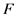 和
和 是
是 和
和 在区间
在区间 上的区间扩张函数。则(4)的实际迭代公式为:
上的区间扩张函数。则(4)的实际迭代公式为:


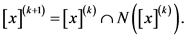
对于区间牛顿法,当 时迭代失败,对此Hansen [9] 拓展了区间牛顿法使其可以处理
时迭代失败,对此Hansen [9] 拓展了区间牛顿法使其可以处理 的情况。但对于
的情况。但对于 的情况目前还没有较好的处理方法,只能用区间二分法避免此情况。
的情况目前还没有较好的处理方法,只能用区间二分法避免此情况。
为了求解区间方程(3),Nikas [1] 对区间牛顿法进行了拓展,我们在这里对其进行简短的说明。
将区间牛顿法换一种表达方式,令: ,
, ,
, ,则区间牛顿法可表示成:
,则区间牛顿法可表示成:
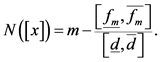 (5)
(5)
根据区间运算法则,(5)可表示为:
 (6)
(6)
令: ,
, ,则(6)的迭代公式是:
,则(6)的迭代公式是:

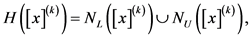

引理2.1 [1] 假设 是(3)定义的含区间参数的区间非线性方程,
是(3)定义的含区间参数的区间非线性方程, 是初始区间,
是初始区间, 是方程
是方程 的零解区间。如果
的零解区间。如果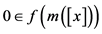 ,且区间
,且区间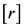 定义如下:
定义如下:
 (7)
(7)
则 总是存在且
总是存在且 (详见图1)。
(详见图1)。
引理2.2 [1] 假设引理2.1的条件成立,如果 且
且 ,
, 的定义同(7),如果
的定义同(7),如果 存在,则
存在,则 (详见图2)。
(详见图2)。




Figure 1. Four cases in lemma 2.1
图1. 引理2.1中的4种情况

Figure 2. Two cases: [r] not existing or existing in lemma 2.2
图2. 引理2.2中[r]不存在与[r]存在的2种情况
对于一些在指定初始区间内非单调的含区间参数的区间非线性方程,由(6)构造的迭代法计算其零解区间时可能会失效。如下例:
例2.1 求区间方程 在初始区间
在初始区间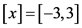 内的零解(精度取
内的零解(精度取 )。考虑到
)。考虑到 ,根据拓展牛顿法可以得到(详见图3):
,根据拓展牛顿法可以得到(详见图3):
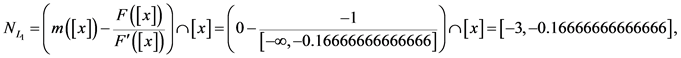


根据例2.1的计算结果我们可以发现: ,则对任意迭代步都有:
,则对任意迭代步都有: ,则每一次迭代得到的
,则每一次迭代得到的 都是一样的,永远达不到要求的精度。这样由(6)构造的迭代法并不能解决这个问题。
都是一样的,永远达不到要求的精度。这样由(6)构造的迭代法并不能解决这个问题。
3. 新的改进算法
为了提高(5)和(6)在求解非单调的区间方程时的计算效率,我们首先把非单调的区间分割成若干个单调的子区间,在每个单调的子区间内再求解(3)的零解区间。
定理3.1 假设 是(3)定义的含区间参数的区间非线性方程,
是(3)定义的含区间参数的区间非线性方程, 是初始区间,
是初始区间, 是
是 的一个零解区间,
的一个零解区间, ,
, 是由(5)和(6)计算得到的,则
是由(5)和(6)计算得到的,则 或
或 。
。
证明:
1) 若 ,则
,则 ,
, 。
。
2) 若 ,则
,则 ,
, 。
。
3) 若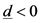 ,
, ,根据Hansen [9] 提出的处理
,根据Hansen [9] 提出的处理 的情况有:
的情况有:
 (8)
(8)
则 ,
,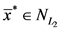 。
。
4) 若 ,
, ,同理有:
,同理有:
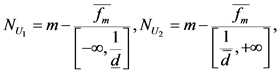 (9)
(9)
则 ,
, 。
。
所以: 或
或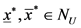 。
。
定理3.1保证了在分割非单调的初始区间时不会丢失区间方程的零解区间的上下界。但是,分割得到的子区间有可能不包含方程的零解区间,对此我们给出定理3.2。
定理3.2 假设定理3.1的条件成立, 是初始区间,若(5)和(6)计算得到的
是初始区间,若(5)和(6)计算得到的 ,
,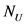 为空,则
为空,则 内不包含
内不包含 的零解。
的零解。
证明:假设 内包含
内包含 的零解,由定理3.1可知:
的零解,由定理3.1可知: 或
或 ,则
,则 ,
, ,与原假设矛盾,定理得证。
,与原假设矛盾,定理得证。
定理3.2保证了不包含零解的区间在迭代中会被自动删除,进而不会影响迭代结果。

Figure 3. Interval equation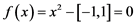 ,
, 
图3. 区间函数 ,
,
定理3.3 假设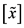 是通过分割初始区间
是通过分割初始区间 得到的一个单调子区间,
得到的一个单调子区间, 是
是 的一个区间零解,
的一个区间零解, ,
, 是
是 的边界函数,
的边界函数, ,
, 分别是建立在
分别是建立在 ,
, 上的区间牛顿算子,若
上的区间牛顿算子,若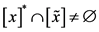 ,则
,则 ,
, 可以以任意精度二阶收敛到
可以以任意精度二阶收敛到 或
或 。
。
证明:因为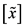 是单调区间且
是单调区间且 ,所以在
,所以在 上解的情况只可能有3种:
上解的情况只可能有3种: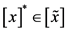 ,
,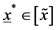 和
和 。对于
。对于 ,
,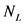 ,
,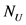 是分别建立在
是分别建立在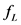 ,
, 上的区间牛顿算子且
上的区间牛顿算子且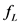 ,
, 是非区间函数,Hansen在文献 [7] 中证明了区间牛顿算子可以以任意精度收敛到非区间函数的零解。同理可证:对于
是非区间函数,Hansen在文献 [7] 中证明了区间牛顿算子可以以任意精度收敛到非区间函数的零解。同理可证:对于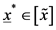 ,
,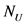 的迭代结果为空,
的迭代结果为空,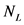 可以以任意精度收敛到
可以以任意精度收敛到 。对于
。对于 ,
, 的迭代结果为空,
的迭代结果为空, 可以以任意精度收敛到
可以以任意精度收敛到 。
。
又Moore在文献 [6] 中证明了区间牛顿算子在逼近单调的非区间方程的零解时是二阶收敛的,故定理得证。
下面给出通过分割非单调区间求解区间方程的零解区间的算法。在如下的算法1中, 用来存储非单调的区间,
用来存储非单调的区间, 的初始值为[x](0),
的初始值为[x](0), 用来存储单调的子区间,
用来存储单调的子区间, 的初始值为空,
的初始值为空,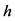 用来取出
用来取出 内不单调的子区间,
内不单调的子区间, 用来将迭代过后的仍不单调的子区间重新存入
用来将迭代过后的仍不单调的子区间重新存入 內,
內,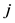 用来将单调的子区间存入
用来将单调的子区间存入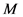 内和取出
内和取出 内单调的子区间,
内单调的子区间,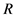 用来存储零解区间,
用来存储零解区间,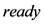 用来决定是否还需要迭代。
用来决定是否还需要迭代。
注:算法1中,第3~7步是将非单调的初始区间分割成若干个单调的子区间(初始区间单调时不执行),第8~9步是对各单调子区间排序,以确保迭代出的r是零解区间,第10~28步是在各单调子区间内计算r。
4. 数值算例
本文所使用的数值算例全部来自 [1] ,计算精度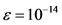 。通过比较初始区间(
。通过比较初始区间( )、迭代步数(
)、迭代步数(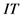 )、
)、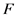 的计算次数(
的计算次数(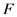 )、
)、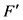 的计算次数(
的计算次数(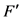 )、二分区间数(
)、二分区间数( )、获得解区间数(
)、获得解区间数( )来比较算法的优劣。表1给出了6个测试函数的具体表现形式,图4给出了每个测试函数的图像,表2是用EIN方法计算得到的结果,表3是用算法1计算得到的结果。
)来比较算法的优劣。表1给出了6个测试函数的具体表现形式,图4给出了每个测试函数的图像,表2是用EIN方法计算得到的结果,表3是用算法1计算得到的结果。
根据表2和表3的计算结果我们能得到:算法1在迭代步数上有明显的减少,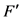 的计算次数有所增加是因为我们需要检测子区间是否单调,如果不单调就需要继续迭代,因此,这一类检测子区间是否单调的
的计算次数有所增加是因为我们需要检测子区间是否单调,如果不单调就需要继续迭代,因此,这一类检测子区间是否单调的 的计算量与
的计算量与 的计算量相同,而算法1的
的计算量相同,而算法1的 的计算次数有明显的改善,总的来说算法1的计算效率高于EIN。
的计算次数有明显的改善,总的来说算法1的计算效率高于EIN。
Table 1. Test function (from reference [1] )
表1. 测试函数(来自参考文献 [1] )



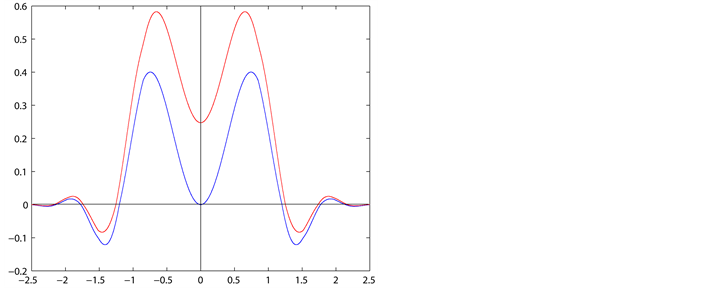
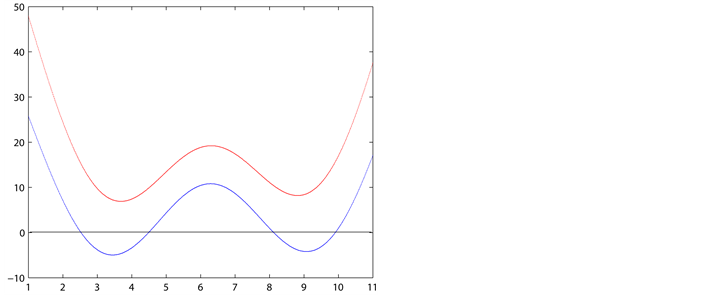
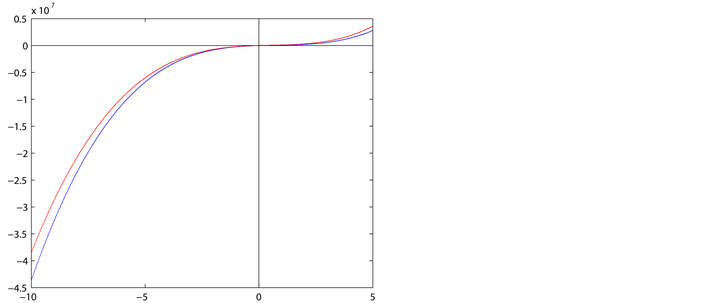
Figure 4. The image of test function
图4. 测试函数的图像
Table 2. Numerical results are calculated by EIN
表2. EIN计算得到的数值结果
Table 3. Numerical results are calculated by algorithm1
表3. 算法1计算得到的数值结果
Continued
5. 总结
本文通过分割非单调的区间得到单调的子区间的方法,对求解含区间参数的区间非线性方程在指定区间内的所有零解区间的拓展区间牛顿算法进行了改进,并且可以解决拓展区间牛顿算法不能解决的问题,在计算效率上也有所提高。
基金项目
本文工作受到江苏省自然科学基金(NO.BK20151139)支持。
文章引用
邱亮,王海军,王琪. 求解区间非线性方程的一类改进算法
A Class of Improved Algorithm for Solving Interval Nonlinear Equation[J]. 应用数学进展, 2017, 06(05): 716-725. http://dx.doi.org/10.12677/AAM.2017.65086
参考文献 (References)
- 1. Nikas, I. and Grapsa, T. (2009) Bounding the Zeros of an Interval Equation. Applied Mathematics and Computation, 213, 466-478. https://doi.org/10.1016/j.amc.2009.03.041
- 2. Balaji, G. and Seader, J. (1995) Application of Interval Newton’s Method to Chemical Engineering Problems. Reliable Computing, 1, 215-223. https://doi.org/10.1007/BF02385253
- 3. Carpani, O. Hvidegaard, L., Mortensen, M. and Schneider, T. (2000) Robust and Efficient Ray Intersection of Implicit Surfaces. Reliable Computing, 6, 9-21. https://doi.org/10.1023/A:1009921806032
- 4. The COPRIN Project (2003) Minimal and Maximal Real Roots of Parametric Polynomials Using Interval Analysis. In: Bliek, C., Jermann, C. and Neumaier, A., Eds., Global Optimization and Constraint Satisfaction, First International Workshop Global Constraint Optimization and Constraint Satisfaction, COCOS 2002, Valbonne-Sophia Antipolis, France, October 2-4, 2002, Revised Selected Papers, Lecture Notes in Computer Science, Vol. 2861, Springer.
- 5. Šiljak, D. and Stipanović, D. (1999) Robust D-Stability via Positivity. Automatica, 35, 1477-1484. https://doi.org/10.1016/S0005-1098(99)00042-4
- 6. Moore, R. (1966) Interval Analysis. Prentice-Hall, Inc., Englewood Cliffs, New Jersey.
- 7. Hansen, E. (1992) Global Optimization Using Interval Analysis. Monographs and Textbooks in Pure and Applied Mathematics, Vol. 165, Marcel Dekker, New York.
- 8. Nikas, I. Sotiropoulos, D. and Grapsa, T. (2006) Extending Interval Newton Method for Nonlinear Parameterized Equations. In: Simos, T., Psihoyios, G. and Tsitouras, C., Eds., ICNAAM-International Conference on Numerical Analysis and Applied Mathematics, Wi-ley-VCH, Hersonisos, Crete, 512-515, ISBN 3-527-40743-X.
- 9. Hansen, E. (1978) Interval Forms of Newton’s Method. Computing, 20, 153-163. https://doi.org/10.1007/BF02252344
