Advances in Applied Mathematics
Vol.06 No.09(2017), Article ID:23091,10
pages
10.12677/AAM.2017.69134
Duality between the Smash Product and Smash Coproduct
Beishang Ren1,2, Yuqiu Wei3, Fenfang Xie2*, Shuai Jin1, Juan Chen1
1Guangdong University of Science & Technology, Dongguan Guangdong
2Guangxi Teachers Education University, Nanning Guangxi
3Guangxi University of Foreign Languages, Nanning Guangxi

Received: Nov. 25th, 2017; accepted: Dec. 14th, 2017; published: Dec. 21st, 2017

ABSTRACT
This paper mainly discusses the relations between module algebra and module coalgebra, comodule algebra and comodule coalgebra. Last, from the comodule coalgebra
contained in
, we further characterize duality between the smash product and smash coproduct.
Keywords:Smash Product, Module Coalgebra, Comodule Coalgebra, Smash Coprodule

Smash积与Smash余积的对偶性
任北上1,2,韦玉球3,谢芬芳2*,金帅1,陈娟1
1广东科技学院,广东 东莞
2广西师范学院,广西 南宁
3广西外国语学院,广西 南宁
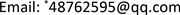
收稿日期:2017年11月25日;录用日期:2017年12月14日;发布日期:2017年12月21日

摘 要
本文探究了模代数与模余代数、余模代数与余模余代数之间的相互关系,并从含于余代数
内的余模余代数
出发,进一步刻画了Smash积与Smash余积的对偶性。
关键词 :Smash积,模余代数,余模余代数,Smash余积

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文中始终约定
为代数闭域,
是
-Hopf代数,
是
-余代数。在Hopf代数文献中,通常采用 [1] 中的Sigma记号:
,及
。
定义1.1 [2] :设
是
-代数。称
为左
-模代数(或
在
上的作用),若下列三条成立:
(MA1)
是左
-模,结构映射
,其中
;
(MA2)
;
(MA3)
。
例1.1:设
是
-代数。如果
是卷积可逆的代数同态,则
是左
-模代数,其中
,
。
在 [1] 中我们知道
可以构成一个
-代数,其中乘法运算为
,这个代数的乘法习惯上称为Smash积。在此基础上, [3] 里又引入了交叉积的概念和一系列重要性质,为Hopf代数的结构理论研究起到了重要作用(譬如,点Hopf代数、辫子Hopf代数等)。由于模代数产生的极大影响引起了学者们的关注,所以又陆续得到了新的对偶概念。
定义1.2 [4] :设
是
-代数。称
为右
-余模代数(或
在
上的余作用),若下列三条成立:
(CA1)
是右
-余模,结构映射
,其中
;
(CA2)
;
(CA3)
。
定义1.3 [4] :设
是Hopf代数,
是
-余代数。称
为左
-模余代数(或
在
上的作用),若下列三条成立:
(MC1)
是左
-模,结构映射
,其中
;
(MC2)
;
(MC3)
。
例1.2:设
是一个
-Hopf代数,而
为
的子Hopf代数。关于
的代数结构的乘法视为模作用,易知
为
-模,进一步可以验证
为
-模余代数。特别地,若取
,可以得到一个平凡的
-模余代数
。
例1.3:易知右
-模
都可以看成左
-模,其中模作用为
,
。进而可推出右
-模代数也可以看成是左
-模代数。类似地,每个右
-模余代数也可以看成是左
-模余代数。
2. 预备知识
首先,讨论模余代数的刻画问题。
命题2.1:设
是Hopf代数,
是
-余代数,且有左
-模结构
。则下列结论等价:
(1)
是一个左
-模余代数;
(2)
是余代数同态;
(3)
的余乘
和余单位
都是
-模同态。
证明:命题条件已经给出(MC1),结论之间的等价性证明如下:
由结论⑴知,条件(MC2)和(MC3)成立,等价于下列等式成立:
(2.1)
(2.2)
其中
是结构映射,我们通常将
简化掉。
注意到,
也是一个余代数,余乘为
,余单位为
。将等式(2.1)和(2.2)箭图化,利用余代数同态的定义及箭图的交换性,即可得知结论⑴和结论⑵等价。
因为
和
都是代数同态,则由
是左
-模可知,
也是左
-模,其中模的结构映射为
由于
是左
-模,则
也是左
-模,结构映射为
现将等式(2.1)和(2.2)恒等变形为
(2.3)
(2.4)
显然,(2.3)和(2.4)事实上就是
和
。
由上文表述所构建的箭图分别为图1和图2。
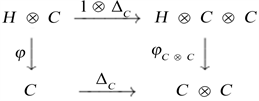
Figure 1. By(2.3) corresponding commutative arrow graph
图1. 等式(2.3)对应的交换箭图

Figure 2. By(2.4) corresponding commutative arrow graph
图2. 等式(2.4)对应的交换箭图
可知,等式(2.1)和(2.2)成立,则相当于图1和图2的交换性分别都成立,即结论(1)和结论(3)等价。
命题2.2:设
和
都是
-Hopf代数,且
为Hopf代数同态。那么
为左
-模余代数(模代数),则
必是左
-模余代数(模代数)。
证明:只对模余代数的情形进行证明,另一情形同理可证。
设
为左
-模余代数,则易知
必是
-模,其中模结构映射为
,即
。于是(MC1)成立。
另外,
即
。所以(MC2)成立。
最后,
。所以(MC3)成立。
如果
为
-空间,
为
的对偶
-空间。若
是左
-模,且
,那么
是右
-模,并且
,其中
类似地,
为右
-模可以得到
为左
-模,其中
。
与
必然具有代数结构不同的是,
-代数
的对偶空间
未必是余代数。但含在
内的
却具
有代数的结构 [1] ,为此,我们有下列结果。
定理2.1:设
为
-Hopf代数,那么
(1)
是一个左
-模代数,那么
是一个右
-模余代数;
(2)
是一个左
-模余代数,那么
是一个右
-模代数。
证明:(1) 因为
是
-代数,则
是
-余代数,欲证(MC1)成立,只需证明
为
的子模即可。也就是说,
。为此,我们将此问题与(MC2)的证明综合考虑。
所以
。上式表明(MC1)和(MC2)都成立。
另外,
,即
,故(MC3)成立。由上可知,
是一个右
-模余代数。
(2) 因为
是左
-模余代数,那么自然知
为代数且
为右
-模,所以(MA1)成立。
下面只需证明(MA2)和(MA3)成立即可。
,
所以
,即(MA2)成立。
最后,由于
,则
进而,
,即(MA3)成立。
所以,
是一个右
-模代数。
推论2.1:设
为Hopf代数,则
自然是一个左
-模代数和左
-模余代数。所以
是一个右
-模余代数,
是一个右
-模代数。
推论2.2:设
为
-Hopf代数,
为反极元;而
为
-代数。那么
可以成为一个左
-模代数,其中模结构映射
,
具有如下等式:
,
。
定义2.1:设
是
-Hopf代数,
是
-余代数。称
为左
-余模余代数,若下列三条成立:
(CC1)
是左
-余模,结构映射
,其中
;
(CC2)
;
(CC3)
。
类似地可以定义右
-余模余代数。
例2.1:设
为Hopf代数,
为余代数,而
是一个余代数同态,如果
作为卷积代数
中的可逆元,那么
必是一个
-余模余代数,其中余模结构映射
,
。
对
-余模余代数的刻画如下:
命题2.3:设
为Hopf代数,余代数
为左
-余模,其中余模结构映射为
,那么
为左
-余模余代数的充分必要条件是
的余乘
和余单位
都是余模同态。
证明:易知,作为
-余模余代数的条件(CC2)和(CC3),分别等价于下列等式:
(2.5)
(2.6)
其中
为同构映射。
另一方面,由于
和
都是余代数同态,故知
和
均为左
-余模,它们的余模结构映射分别为:
由此可知,
构成左
-余模同态当且仅当
,即(2.5)成立;
构成左
-余模同态当且仅当
,即(2.6)成立。
在
-模代数的讨论中我们曾引入了Smash积的概念,在
-余模余代数中我们也可以对偶地讨论
Smash余积。
定义2.2 设
为Hopf代数,
是一个左
-余模余代数,那么可以构造
和
的Smash余积
,其中,作为
-空间,
,
中的元素记为
。另外,在
中定义余乘
,
以及余单位
。
定理2.2:设
为Hopf代数,
为左
-余模余代数,那么Smash余积
关于给定的
余乘和余单位构成一个余代数。
证明:
另一方面,
所以,
。
最后,
所以,
.
已知当
是左
-模时,那么
必然能成为右
-模。习惯上记
为
中的最大有理子模(或
中所有有限维子模的和)。
定理2.3:设
为Hopf代数,那么
(1)
是一个左
-余模余代数,则
是一个右
-余模代数;
(2)
是一个有限维的左
-余模代数,则
是一个右
-余模余代数。
证明:因为
是一个有限维的,所以
,(2)的证明显然 [5] 。
(1) 只需证明
是
的子代数即可。
设余模
的结构映射为
,令
是
的余模结构并给出赋值映射
,其中
。如果由有理模的定义可知
,那么
存在
使得
由有理模的性质可知,这里
。又条件
表明存在
使得
,即单位元
。
设
,那么
这表明
存在,即
对乘法封闭。
3. 主要定理
如果
为左
-余模,那么
就是有理右
-模;同时
也是左
-模,其中模的结构映射是限制
。
定理3.1:设
是
-余代数。如果
是左
-余模余代数,将
对左
-模
的作用限制在
上,那么
(1) 作为代数并具有左
-模结构的
是一个左
-模代数;
(2) 同态单射
是一个代数同态,其中
。
证明:(1) 显然,只需证明(MA1),(MA2)成立即可。
所以,(MA1)成立。
即,(MA2)成立。
(2) 由定理2.2可知
是余代数,进而
是一个代数;显然
是个代数。而
的单射性是自然的。现只需论证
保持单位元和乘法即可,而等式的验证工作较易。
设
为左
-模代数,
的反极元为
。注意到
和
,
,
都是代数同态,易知当
是
的余有限维理想,则
及
分别是
和
的余有维限理想。而且
的余有限维理想
还是
的左
-子模,因为
,
另外,由于
是含在
内的余代数,设
,
是
的某个余有限维理想而且还是
的左
-子模,那么
是
的子余代数,这是因为作为
的子模
,所以有
定理3.2:设
是左
-模代数。模结构映射
。那么
(1)
且
形成一个左
-余模,其中
是一个限制;
(2) 余模
是一个左
-余模余代数;
(3) 嵌入映射
是一个余代数同构。
证明:(1)设
,那么存在
的某个余有限维理想
使得
。所以
自然能零化
,这说明,
。设
,那么
,
,
,其中
是该等式成立的最小正整数。进而易知:
是线性无关,令
,那么
自然就是
的余有限维子空间,则有
这表明
是
的右理想。所以
,即
。
最后,
所以,
构成一个左
-余模。
(2) 欲证左
-余模
是一个左
-余模余代数,关键是证明(CC2)~(CC3)都成立。事实上,
,
,
,于是有
另一方面,还可以有
这就恰好表明
即,(CC2)成立。而(CC3)成立是显然的,因为易知有
。
(3) 显然,
。另外,
我们有
所以,
。
基金项目
广西研究生教育创新计划资助项目(JGY2014092);广东科技学院科研项目及青年项目(GKY-2016KYYB-15, GKY-2017KYQN-4);广东科技学院2016年“质量工程”项目。
文章引用
任北上,韦玉球,谢芬芳,金 帅,陈 娟. Smash积与Smash余积的对偶性
Duality between the Smash Product and Smash Coproduct[J]. 应用数学进展, 2017, 06(09): 1105-1114. http://dx.doi.org/10.12677/AAM.2017.69134
参考文献 (References)
- 1. Sweedle, M.E. (1969) Hopf Algebra. Benamin, New York.
- 2. Cohen, M. (1986) Hopf Algebra Actions. Journal of Algebra, 100, 363-379.
https://doi.org/10.1016/0021-8693(86)90082-7
- 3. Montgomery, S. (1993) Hopf Algebras and Their Actions on Rings. CBMS Regional Conference Series in Math, 82, Amer. Math. Soc., Providence.
- 4. Blattner, R.J., Cohen, M. and Montgomery S. (1986) Crossed Products and Inner Actions Hopf Algebras. Transactions of the American Mathe-matical Society, 298, 671-711.
https://doi.org/10.1090/S0002-9947-1986-0860387-X
- 5. Zhang, Z.H., Wang, Z.W., Ren, B.S. and Zhang, L.Y. (2013) The Structure of Weak Hopf Module Coalgebras. Journal of Nanjing University Mathematical Biquarterly, 30, 1-12.