Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24616,7
pages
10.12677/AAM.2018.74045
Research on Expressway Toll Capacity
Wushuang Tan1*, Yi Yuan1, Yi Lei2
1College of Mathematics and Software Science, Sichuan Normal University, Chengdu Sichuan
2College of Computer Science, Sichuan Normal University, Chengdu Sichuan

Received: Apr. 8th, 2018; accepted: Apr. 20th, 2018; published: Apr. 27th, 2018

ABSTRACT
In this paper, the duplicate toll plazas and fan toll plazas are investigated through the analysis of express toll access and fan toll access, respectively. The mathematical models are found to discuss the optimum construction scheme under different traffic flows and the toll plaza area of different shapes. And then the result is obtained that the area of duplicate toll plaza is smaller than that of the fan toll plaza. Finally, it is found that the conversion of the traditional man-made toll form into MTC and ETC substantially improves the throughput of the toll station.
Keywords:Duplicate Toll Access, Fan-Shaped Toll Access, Toll Plaza
高速公路收费站通行能力研究
谭武霜1*,袁艺1,雷怡2
1四川师范大学数学与软件科学学院,四川 成都
2四川师范大学计算机科学学院,四川 成都

收稿日期:2018年4月8日;录用日期:2018年4月20日;发布日期:2018年4月27日

摘 要
本文通过高速公路复式收费通道和扇形式收费通道的分析,分别讨论了复式收费广场和扇形式收费广场,通过建立数学模型讨论了不同交通流量下最优的建设方案以及不同形状的收费广场占地面积。然后获得了复式收费广场的占地面积小于扇形收费广场。最后发现将传统人工收费形式变为MTC与ETC极大地提高收费站的吞吐量。
关键词 :复式收费通道,扇形式收费通道,收费广场

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
不同的收费通道对停车收费的效率,收费障碍区域的道路通行能力有不同的影响。本文细致研究了不同形式的收费通道对高速公路收费障碍区域吞吐量的影响,为收费广场最优形式的确定提供了有力的依据。
2. 复式收费通道
复式收费通道 [1] 是在一条收费道路上串联多个收费亭(如下图),让多个车辆同时收费的收费通道,正在接受服务队列中收费时间最长的车辆决定整个队列的服务时间,收费亭的个数同时影响着车辆在收费亭服务的排队时间、收费时间、驶入收费障碍区域的时间,驶离收费障碍区域的时间等。
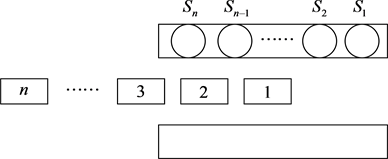

在车流量较大的情况下,假定单位时间(h)通过1500列队的车辆数,排队车辆依次序按列队驶入收费通道并接受服务,未出现途中变道的情况,且每批服务的车辆数等于收费亭的个数。
本文运用时间驱动的方法 [2] [3] 模拟服务1500列队车辆通过收费障碍区域的平均滞留时间来衡量其通行能力。设串联收费亭的数目为m,驶入收费障碍区域的车辆速度为v,车辆启动的反应时间为t,一个列队的车辆平均收费时间T,收费亭间距L,等待收费车辆车头间距为l,收费阻碍区域停留时间包括车辆驶入时间 、收费服务时间 和列队最后一辆车离开启动时间R。第i辆车进入收费通道的时间: ;第i辆车行驶至第i个收费亭所走路程的计算式如下: ;第i辆车驶入收费
通道的行驶时间计算公式如下: 。因此,第i辆车的驶入就位时间计算公式如下:
车辆收费时间
服从负指数分布,其密度函数为:
利用反函数法编写服从负指数的n个随机数。第i辆车的收费结束时间计算公式如下: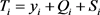 。
。
收费亭为n个复式收费通道,列队每辆车的服务时间与其相应的驶入就位时间之和的最大值为该列队的最大收费结束时间,列队车辆最大收费结束时间计算公式为: 。正在接受服务队列中收费时间最长的车辆决定整个队列的服务时间,因此若第k个车辆收费用时最多,只用算 辆车的启动时间,那么列队的总启动时间为: 。故第k个列队车辆滞留时间为:
将所有列队车辆服务时间相加求平均值即得到总的平均滞留时间。本文只考虑单通道上车辆滞留时间,多通道乘以收费通道数即可,由美国交通统计局统计数据 [4] 可知,车辆启动时间t约为0.5 s,两收费亭的距离L约为9 m,相邻车头间距l为6 m,通道内的车辆平均速度v为5 km/h。由于收费站的个数为通行车道数的两倍,故只考虑一个收费通道串联两个收费亭,即 。将数据带入模型中,求得1500个队列的滞留时间,其中前十个的滞留时间如下表所示。
即得到1500个队列的滞留平均时间 。
3. 扇形式收费通道
扇形式收费通道即是在收费障碍区域中单路排队多通道服务(如下图),车辆列队等候依次驶入该车道对应的收费亭,在车流量比较大的时候,行车道路的车辆有两个收费亭选择,从而减少排队时间,但是当通道流出的车流量大于出站口的最大车流量容纳能力,便会在出口处出现拥挤状况。该收费通道的通行能力主要受到收费服务水平、合并模式的影响,于是只可考虑收费前排队等候时间 、收费过程中的排队等候时间 。假设汽车到达的时间间隔符合负指数分布,收费服务时间服从负指数分布,汽车到达收费站是服从负指数分布。车辆在m个收费车道中分别排队,车辆一旦进入某个收费车道不可再更改车道 [2] 。


每个服务通道收费员的服务强度u,平均服务时间为 ,单位时间达到的车辆数λ, 为t时刻有k辆车的概率,收费亭的数目为N, 为系统空闲概率(系统处于没有顾客来到要求服务的概率), 为系统负荷水平(交通强度或服务程度)。本文考虑在平稳状态下的概率分布情况,即 的情况 [2] 。
扇形式通道系统有C个通道的个数,收费亭的个数为2C,则系统的服务强度为: 。系统中有n个单位(汽车)进入的概率为:
系统中收费亭空闲的概率为: ,即排队长度为: ,排队中平均等待时间: ,系统中平均服务的时间: ,滞留收费广场总时间的期望值:
其中 。
只考虑一条行车道选择最近的两个收费亭的情况,每小时通过的车辆数为3000,据美国交通统计局统计数据,取平均后,新泽西州高速公路车辆流的数据如下: 。将数据带入模型中 cars/s, car/s, , 故该系统稳定,求得滞留收费广场的总时间为 。
4. 成本分析
基于对高速公路收费站安全影响因素的分析,选择收费广场渐变率( ),收费站服务水平( )与收费广场入口段纵坡(i)作为模型参数,并以收费站年交通事故发生次数为安全评价模型的标度(Y)。建立事故预防评价线性模型:
其中 。
在此只考虑土地成本,设备成本和单主路情况。假设土地面积包括收费通道(将收费通道长度近似用收费岛长度代替)和收费广场过渡段(连接高速公路基本路段和收费通道的等腰梯形区域),梯形区域的边与高速公路基本路段的夹角为 ,道路宽度 ,收费岛宽度 ,(如下图)梯形下底长度
 ,其中n为收费站个数,主路宽度d,梯形长度
,收费岛长度l。
,其中n为收费站个数,主路宽度d,梯形长度
,收费岛长度l。


4.1. 复式收费广场
基于收费站的个数与主路道路个数相同,则 。为减少收费站中前车的交易时间对后车的影响,在两收费亭之间设置20 m的缓冲长度 ,因此收费广场面积为:
其中 。
4.2. 扇形收费广场
基于收费站的个数是主路道路的两倍,则 。收费面积为:
其中 。
5. 模型求解
X为收费站设计和交通运行参数矩阵, 代表第i个样本的收费站年交通事故次数,β为系数矩阵,则样本可用下面的矩阵表示:
根据国内外相关研究成果和实际建设经验,建议收费广场渐变率( )取值在1/7~1/10之间,收费站服务水平( )取值在0.7~0.9之间,收费广场入口段纵坡(i)取值在1.0%~2.0%之间,取渐变段长度为
标准值50 m,则由 可求得复式收费广场和扇形收费广场不同的渐变率。
5.1. 复式收费广场
对于复式收费广场而言,由于渐变率为渐变道路加宽宽度与渐变道路的比值,模型表达式为
取 , , 。对系数矩阵标准化处理后进行极大似然估计,可得到一个正规方程组: 。β的极大似然估计为:
带入可得到回归方程:
将 标准化得到的数据带入回归方程得到 。
5.2. 扇形收费广场
取 , , 。对系数矩阵进行极大似然估计,可得到一个正规方程组: 。则β的极大似然估计为:
带入可得到回归方程:
将 标准化后带入回归方程得到 。
在的收费广场渐变率,服务水平,入口段纵坡相同的情况下,复式收费广场发生事故的几率小于扇形收费广场。
5.3. 成本分析模型求解
由大量数据统计以及相关研究 [1] 可以得到一般人工收费站的道路宽度 ,收费岛宽度 ,主路宽度 ,收费岛长度 ,梯形区域的边与高速公路基本路段的夹角取为 ,缓冲长度 。带入数据得到复式收费广场面积为: 。带入数据得到扇形收费广场面积为: 。
通过不同形状的收费广场占地面积来反映成本,由计算结果可知复式收费广场的占地面积小于扇形收费广场。
在本文的假设中,当在设计收费广场时,若更看重道路的吞吐量,综合考虑,使用扇形收费站更佳。
根据实际情况给吞吐量,事故预防和土地成本赋予不同的权重,则得到相适应的解决方案。
6. 仿真方案设定
将传统人工收费形式变为MTC与ETC的实质是将改变了收费站服务水平,收费站服务水平的提升将极大地提高收费站的吞吐量。因此,为了便于比较分析ETC系统对收费站服务水平的影响程度,选择ETC车道数量,ETC使用率和交通流量三个参数构造仿真方案 [5] 。仿真结果分析:选取仿真方案中ETC使用率为30%、60%和90%的收费站平均延误仿真结果进行分析。
当ETC使用率为30%时,可知:当交通流量 < 1000 veh/h时,配置1条ETC通道收费服务水平最佳,即ETC和MTC的比率为1:3;当交通流量 > 1000 veh/h时,配置2条ETC通道服务水平最佳,即ETC和MTC的比率为1:1。
当ETC使用率为60%时,可知:当交通流量 < 1400 veh/h时,配置1条ETC通道收费服务水平最佳,即ETC和MTC的比率为1:3;当交通流量 > 1400 veh/h时,配置2条ETC通道收费服务水平最佳,即ETC和MTC的比率为1:1。
总体而言配置1、2、3条ETC通道均可以提高收费站服务水平。
当ETC使用率为90%时,可知:配置3条ETC通道收费站服务水平最佳,配置2条也可,即ETC和MTC的比率为3:0或2:1。
文章引用
谭武霜,袁 艺,雷 怡. 高速公路收费站通行能力研究
Research on Expressway Toll Capacity[J]. 应用数学进展, 2018, 07(04): 362-368. https://doi.org/10.12677/AAM.2018.74045
参考文献
- 1. 程俊龙. ETC-MTC混合式收费站通行能力研究[D]: [硕士学位论文]. 成都: 西南交通大学, 2015.
- 2. 田根平. 高等级公路收费站通行能力评价研究[D]: [硕士学位论文]. 昆明: 昆明理工大学, 2008.
- 3. 刘伟铭. 道路收费系统的优化方法研究[D]: 博士学位论文. 北京: 国防科学技术大学, 2004.
- 4. Kai, N. and Schreckenberg, M. (1992) A Cellular Automaton Model for Freeway Traffic. Journal De Physique I, 2, 2221-2229.
- 5. 张晨琛, 王艳辉, 贾利民. ETC系统对收费站服务水平的影响研究[J]. 交通运输系统工程与信息, 2013, 13(2): 147-152.
NOTES
*通讯作者。