Advances in Applied Mathematics
Vol.
07
No.
10
(
2018
), Article ID:
27251
,
10
pages
10.12677/AAM.2018.710150
Study on Stability and Hopf Bifurcation of FHN-ML Neuron System
Haonan Xu, Shengwen Deng
School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou Gansu

Received: Oct. 1st, 2018; accepted: Oct. 17th, 2018; published: Oct. 24th, 2018

ABSTRACT
Based on the FHN-ML model of electro synaptic coupling neurons, the stability near the equilibrium point and the equilibrium point of the system are discussed. The existence of Hopf bifurcation and the direction of Hopf bifurcation are proved by using the normal form theory and Hassard method. The periodic solution and approximate period are given. Finally, this paper uses numerical simulation tools such as MATLAB, C language to study the bifurcation behavior and dynamics of the model under a single parameter, verify the interference of external stimuli on the neural system model, and apply the final conclusion to provide a theoretical basis for neuron physiological experiments.
Keywords:FHN-ML Model, Hopf Bifurcation, Stationary Points, Stability, Direction of Branching
FHN-ML神经元系统的稳定性及Hopf分岔研究
续浩南,邓生文
兰州交通大学数理学院,甘肃 兰州

收稿日期:2018年10月1日;录用日期:2018年10月17日;发布日期:2018年10月24日

摘 要
基于电突触耦合神经元FHN-ML模型,讨论了该系统的平衡点及平衡点附近的稳定性,利用范式理论、Hassard等人降维方法,证明了系统Hopf分岔的存在并且确定了Hopf分岔的方向,给出了周期解与近似周期。最后,利用Matlab、C语言等数值模拟工具研究模型在单个参数下的分岔行为及动力学现象,验证了存在外界刺激对神经系统模型的干扰作用,应用最终的结论为神经元生理学实验提供理论依据。
关键词 :FHN-ML模型,Hopf分岔,平衡点,稳定性,分岔方向

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在一完整的生物系统中,其神经系统是由大量高度内联的神经元细胞构成的。神经元之间的信息传递是通过细胞膜间动作电位的变化实现的 [1] 。近半个世纪,医学专家通过医学实验将神经元的信息传递规律用微分方程的形式表现出来。近几年,国内外学者通过对神经元系统的研究和数值模拟,发现神经元系统发生Hopf分岔的仿真结果表明细胞膜受刺激后产生连续动作电位的异变波形同医学实验中观察到的病变现象十分相似 [2] ,说明生理参数变化引发神经系统分岔可能是肌肉疾病的诱因。
在神经元模型中,FHN模型和ML模型具有简易性和现象丰富性的特点,因此它们经常应用于各种科学研究及验证。Morris等首次提出ML模型,随后很多学者把神经元膜电位方程中的外界刺激电流变为由动力学方程控制的变量,将模型改进成三维ML模型,从而进一步研究外界刺激带来的神经元复杂动力学现象 [3] 。其次,FitzHugh和Nagumo等共同提出FHN模型,并研究了外界周期脉冲激励下,神经元系统产生的随机整数倍和混沌多峰放电节律的关系,表明了两类节律的动力学特性 [4] [5] 。另外,近年来,国内杨雨潼 [4] 等以FHN和ML神经元模型为基础,通过两个神经元的电耦合,构建FHN-ML模型,基于FHN-ML模型,研究了外界刺激和时滞对FHN-ML模型发放模式的影响。
本文以FHN-ML模型为基础,首先分析系统的平衡点及其稳定性,利用范式理论,分析Hopf分岔的存在性并且确定分岔方向,并给出近似周期解与近似周期。最后,利用数值模拟方法研究模型在单个参数下的分岔行为及动力学现象,验证了存在外界刺激对神经系统模型的干扰作用,应用最终的结论为神经元生理学实验提供理论依据。
2. 模型描述
在参考文献 [4] ,以FHN和ML两个神经元模型为基础,通过电突触耦合,构建出FHN-ML神经元模型:
(1)
(2)
(3)
(4)
(5)
其中,
(6)
(7)
(8)
、 分别代表FHN神经元和ML神经元的膜电位;C表示膜电容;Y、 分别表示FHN神经元和ML神经元的恢复变量;I表示慢变调节电流, 为时间尺度因子,取值为0.005; 是两个神经元之间的连接强度。 、 、 、 、 、 分别表示钙离子通道、钾离子通道、漏电流通道的最大电导和反转电压; 、 分别是钙离子通道和钾离子通道打开的概率的稳态值; 为激活时间常数; 、 分别表示依赖于电压的 和 斜率的倒数; 、 是依赖于 和 的系统参数。
3. 系统平衡点及其稳定性
3.1. 平衡点
一个系统的平衡点指的是那些系统状态不依赖于时间t而发生改变的那些点,因此我们可以通过求解系统的零线从而进一步判断系统的稳定状态与向量场。首先,令式子(1) = (2) = (3) = (4) = (5) = 0,可以得到关于该系统平衡点的表达式 。其中, , ,
, 。而 满足式子:
根据卡尔丹公式,上述一元三次方程的判别式为:
故 恒有一个实数解,进一步可以求解出该神经元系统的平衡点。因此,系统恒有一个平衡点。
3.2. 平衡点附近的稳定性
通过前面分析,已经求解出系统的平衡点,接下来继续分析模型平衡点附近的稳定性。首先,在平衡点 附近线性化该系统,可得到一个五阶的Jacobian矩阵 :
其中 、 的表达式如下:
, ,
,
。
最后进一步计算得到Jacobian矩阵的特征方程
(9)
其中,
,
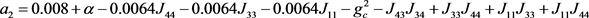 ,
,
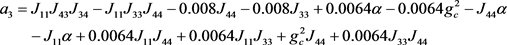 ,
,
 ,
,
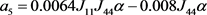 。
。
然后通过数学计算软件得到上述特征方程的特征值,进一步根据特征值的正负与根的类型来判断该平衡点的稳定性及其类型。
3.3. 数值模拟
进一步,给出不同参数的数值来讨论平衡点附近的稳定性。
选取 、
、 、
、 、
、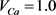 、
、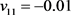 、
、 、
、 、
、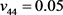 、
、 、
、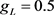 、
、 ,可以求得平衡点
,可以求得平衡点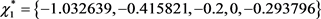 ,该平衡点对应的特征值为:
,该平衡点对应的特征值为: 。因为特征值为一对具有负实部的共轭特征根和三个正实根,故平衡点附近是非渐进稳定的,在此处它是一个不稳定的螺旋点或者焦点,在该点附近系统的相轨迹不会趋于该点。
。因为特征值为一对具有负实部的共轭特征根和三个正实根,故平衡点附近是非渐进稳定的,在此处它是一个不稳定的螺旋点或者焦点,在该点附近系统的相轨迹不会趋于该点。
当参数选取情况如下: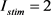 、
、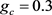 、
、 、
、 、
、 、
、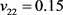 、
、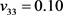 、
、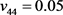 、
、 、
、 、
、 ,该状态下平衡点
,该状态下平衡点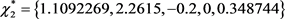 ,特征根为:
,特征根为: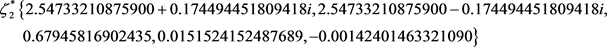 。因为特征值是一对具有正实部的共轭特征根和两个正实根与一负实根,故平衡点附近是非渐进稳定的,其对应于生理学现象是细胞膜电位去极化过程中的某个暂态平衡,膜电位经过该点的去极化过程,恢复成静息状态。
。因为特征值是一对具有正实部的共轭特征根和两个正实根与一负实根,故平衡点附近是非渐进稳定的,其对应于生理学现象是细胞膜电位去极化过程中的某个暂态平衡,膜电位经过该点的去极化过程,恢复成静息状态。
另一组参数选取情况为: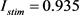 、
、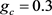 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ,该状态下平衡点
,该状态下平衡点 。其特征值为:
。其特征值为: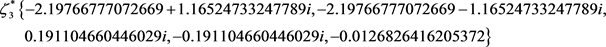 。因为该平衡点有三个负实部特征值,且另两个特征值是零实部的共轭根,故它是一个非双曲的平衡态,神经元系统在平衡点附近的状态结构不稳定,任意小的刺激扰动都会导致平衡点的消失或者改变平衡点附近的拓扑结构。
。因为该平衡点有三个负实部特征值,且另两个特征值是零实部的共轭根,故它是一个非双曲的平衡态,神经元系统在平衡点附近的状态结构不稳定,任意小的刺激扰动都会导致平衡点的消失或者改变平衡点附近的拓扑结构。
综上所述,该神经元系统在平衡点 与
与 附近会失去稳定性,其状态轨线会发生偏移。而当系统参数变化时,平衡点
附近会失去稳定性,其状态轨线会发生偏移。而当系统参数变化时,平衡点 处系统的拓扑结构会发生变化,表现为结构的不稳定性,它对系统的影响特性较大。
处系统的拓扑结构会发生变化,表现为结构的不稳定性,它对系统的影响特性较大。
4. Hopf分叉的稳定性及分岔方向
4.1. 理论分析
在这一部分中,主要研究了当平衡点附近出现一对复共轭特征值时,系统的状态改变情况。而当模型出现Hopf分岔,系统的周期轨道流消失或者出现,即系统从稳态变化到振荡状态(或者从振荡状态变化到稳态),而这是衡量系统现象的一个重要机制。
出自于上述目的,首先从线性化Jacobian矩阵所得到的特征方程(9)进行分析。为了满足Hopf分叉的存在条件及横截性条件,我们首先考虑上述特征方程(9)关于分岔参数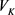 的导数,
的导数,

假定存在一复特征值: ,解方程
,解方程 ,并且将其实部与虚部分离可得:
,并且将其实部与虚部分离可得:
 ,
,
其中,




由上式可得 。当满足
。当满足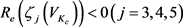 ,根据Poincare-Andronov-Hopf理论,可知该神经元系统在
,根据Poincare-Andronov-Hopf理论,可知该神经元系统在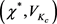 会发生Hopf分岔。
会发生Hopf分岔。
若该特征值为纯虚数: ,Hopf分岔所满足的条件为:
,Hopf分岔所满足的条件为: 与
与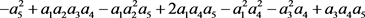 ,上述分别为应用到了横截条件与Roth-Hurwitz判据。
,上述分别为应用到了横截条件与Roth-Hurwitz判据。
最后,应用Hassard,Wan [6] [7] 方法,在分岔参数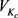 附近分析系统Hopf分岔稳定性与分岔方向。若该系统特征值存在一共轭对,满足
附近分析系统Hopf分岔稳定性与分岔方向。若该系统特征值存在一共轭对,满足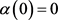 ,
, 。存在一变换P使得Jacobian矩阵
。存在一变换P使得Jacobian矩阵 变成如下形式:
变成如下形式:

矩阵P定义如下: ,
,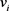 表示其特征值所对应的特征向量。
表示其特征值所对应的特征向量。
做代换 ,
, ,原神经元系统表示为
,原神经元系统表示为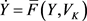 。应用Hassard方法 [6] [7] 可得以下式子:
。应用Hassard方法 [6] [7] 可得以下式子:
 ,
, ,
,
 ,
, ,
,
 ,
, ,
,
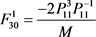 ,
,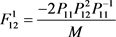 ,
,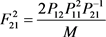 ,
, ,
,
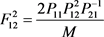 ,
, ,
, ,
, ,
,
 ,
,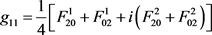 ,
,
 ,
, ,
,
 。
。
综上,可得下面三个判断分岔的重要式子:
 ,
, ,
,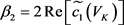
当系统的分岔参数通过临界值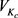 时,其会经历Hopf分岔,并出现下列特性:
时,其会经历Hopf分岔,并出现下列特性:
1) 若 ,Hopf分岔为超临界(亚临界);2)
,Hopf分岔为超临界(亚临界);2)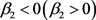 ,分岔周期解轨道是稳定(不稳定);3)
,分岔周期解轨道是稳定(不稳定);3)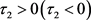 周期解的周期增加(减少)。
周期解的周期增加(减少)。
模型系统有唯一振幅周期解,周期为 ;周期解近似为:
;周期解近似为: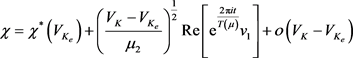 。
。
4.2. 数值模拟
将4.1节的Hopf理论应用于实际的数值模拟仿真中。首先,选取K+的反转电压 为分岔参数,其他参数为
为分岔参数,其他参数为 、
、 、
、 、
、 、
、 、
、 、
、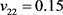 、
、 、
、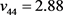 、
、 、
、 ,在该状态下系统对应的特征值为:
,在该状态下系统对应的特征值为:
 。经计算发现
。经计算发现 ,可知该神经元系统发生Hopf分岔。故存在矩阵P如下:
,可知该神经元系统发生Hopf分岔。故存在矩阵P如下:

使得Jacobian矩阵 变成上述的准对角线形式。然后,应用Hassard等人的降维方法,计算出决定分岔方向的几个参数如下:
变成上述的准对角线形式。然后,应用Hassard等人的降维方法,计算出决定分岔方向的几个参数如下: ;
;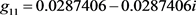 ;
; ;
; ;进一步计算得
;进一步计算得 。最后,Hopf分岔方向的三个参数为
。最后,Hopf分岔方向的三个参数为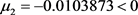 ;
; ;
; 。根据数值结果,Hopf分岔是超临界的。已知
。根据数值结果,Hopf分岔是超临界的。已知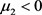 ,分岔方向的存在于范围
,分岔方向的存在于范围 。进一步,
。进一步, ,可以得到系统解是一个周期增加的渐进稳定轨道。系统振幅的周期为
,可以得到系统解是一个周期增加的渐进稳定轨道。系统振幅的周期为 ,周期近似解为:
,周期近似解为:

5. 分岔及混沌的数值仿真
根据以上理论分析,系统所发生的分岔会随着参数选取的不同而发生改变。固定某些参数,选取其中某些参数作为分岔参数可以得到相应的Hopf分岔图和倍周期分岔图,同时也可以观察到系统丰富的动力学现象。
5.1. 对于K+最大电导的数值仿真
1) 当固定 、
、 、
、 、
、 、
、 、
、 、
、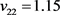 、
、 、
、 、
、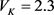 、
、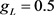 、
、 ,代表K+最大电导的参数
,代表K+最大电导的参数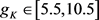 变化时,该神经元系统的数值仿真如图1(a)。随着参数
变化时,该神经元系统的数值仿真如图1(a)。随着参数 的逐渐增大,系统的稳定性也在不断变化。随着K+最大电导的增大系统出现倍周期现象,并出现混沌状态。随即又出现了多周期与混沌状态交替出现的行为。
的逐渐增大,系统的稳定性也在不断变化。随着K+最大电导的增大系统出现倍周期现象,并出现混沌状态。随即又出现了多周期与混沌状态交替出现的行为。
2) 当固定该系统的其他参数 、
、 、
、 、
、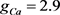 、
、 、
、 、
、 、
、 、
、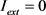 ,参数
,参数 变化时,系统动力学行为如图1(b)。随着参数
变化时,系统动力学行为如图1(b)。随着参数 的逐渐增大,系统由单周期状态进入倍周期—混沌状态,然后逆倍周期变化进入二周期状态。系统在经历倍周期—混沌—逆倍周期复杂的反复动力学行为后,最后达到一周期的稳定运动状态。所以,在其他条件一定的状态下将K+最大电导控制在某些范围内,该电耦合的神经元系统会进入稳定状态。
的逐渐增大,系统由单周期状态进入倍周期—混沌状态,然后逆倍周期变化进入二周期状态。系统在经历倍周期—混沌—逆倍周期复杂的反复动力学行为后,最后达到一周期的稳定运动状态。所以,在其他条件一定的状态下将K+最大电导控制在某些范围内,该电耦合的神经元系统会进入稳定状态。
 (a)
(a)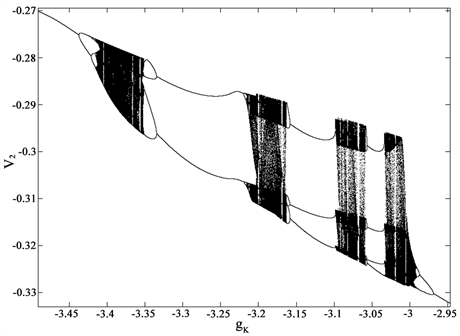 (b)
(b)
Figure 1. Dynamic bifurcation diagram of parameters gK
图1. 参数gK的动力学分岔图
5.2. 对于外界交流电频率的数值仿真
1) 当选择参数 、
、 、
、 、
、 、
、 、
、 、
、 、
、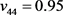 、
、 、
、 、
、 、
、 ,外界交流电频率参数
,外界交流电频率参数 变化时,该神经元系统的数值仿真如图2(a)。随着参数
变化时,该神经元系统的数值仿真如图2(a)。随着参数 的逐渐增大,系统的稳定性也在不断变化。参数
的逐渐增大,系统的稳定性也在不断变化。参数 逐渐增大,系统在经历倍周期—混沌—逆倍周期动力学行为后,最后达到二周期的稳定运动状态。当参数
逐渐增大,系统在经历倍周期—混沌—逆倍周期动力学行为后,最后达到二周期的稳定运动状态。当参数 变化时,其数值仿真如图2(b),系统呈现出另一种动力学行为:Hopf分岔现象。
变化时,其数值仿真如图2(b),系统呈现出另一种动力学行为:Hopf分岔现象。
2) 另外界交流电 ,其他参数
,其他参数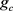 、
、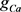 、
、 、
、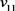 、
、 、
、 、
、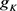 、
、 、
、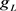 、
、 同上,参数
同上,参数 。频率
。频率 变化时,系统动力学行为如图2(c)。系统在经历倍周期—混沌—逆倍周期复杂的反复动力学行为后,最后达到一周期的稳定运动状态呈现出与上面不一样的现象。
变化时,系统动力学行为如图2(c)。系统在经历倍周期—混沌—逆倍周期复杂的反复动力学行为后,最后达到一周期的稳定运动状态呈现出与上面不一样的现象。
3) 外界交流电 ,其他参数
,其他参数 、
、 、
、 、
、 、
、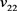 、
、 、
、 、
、 、
、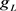 、
、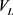 同上,参数
同上,参数 。频率
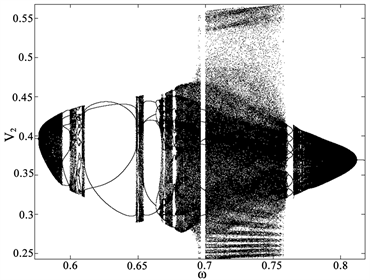
。频率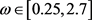 变化时,其单参分岔行为如图2(d)。随着外界交流电频率的增大,系统出现倍周期—混沌现象,随机出现了周期—混沌交替的动力学现象。
变化时,其单参分岔行为如图2(d)。随着外界交流电频率的增大,系统出现倍周期—混沌现象,随机出现了周期—混沌交替的动力学现象。
 (a)
(a) 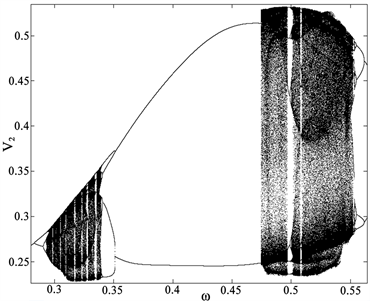 (b)
(b)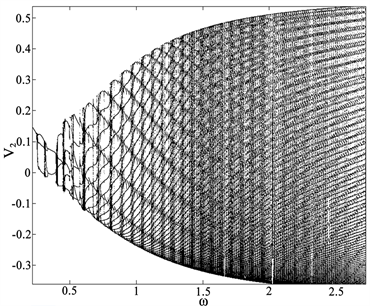 (c)
(c) (d)
(d)
Figure 2. Dynamic bifurcation diagram of parameters ω
图2. 参数ω的动力学分岔图
6. 结束语
首先分析了电耦合神经元系统FHN-ML模型的平衡点及其附近的稳定性,发现系统恒有一实数平衡点。其次,我们利用Hassard等人的高维系统降维方法,讨论了系统Hopf分岔的存在性并且确定了Hopf分岔的方向,并给出近似周期解与近似周期。得到了一个超临界的Hopf分岔,确定系统解是一个周期增加的渐进稳定轨道。在数值模拟过程中,以 为分岔参数,给出了满足条件的一个Hopf分岔。最后,利用C语言、Matlab等工具研究模型在单个参数下的分岔行为及动力学现象,验证了存在外界刺激对神经系统模型的干扰作用,应用最终的结论为神经元生理学实验提供理论依据。
为分岔参数,给出了满足条件的一个Hopf分岔。最后,利用C语言、Matlab等工具研究模型在单个参数下的分岔行为及动力学现象,验证了存在外界刺激对神经系统模型的干扰作用,应用最终的结论为神经元生理学实验提供理论依据。
文章引用
续浩南,邓生文. FHN-ML神经元系统的稳定性及Hopf分岔研究
Study on Stability and Hopf Bifurcation of FHN-ML Neuron System[J]. 应用数学进展, 2018, 07(10): 1289-1298. https://doi.org/10.12677/AAM.2018.710150
参考文献
- 1. 陈良泉. Hodgkin-Huxley模型的分岔分析与控制[D]: [硕士学位论文]. 天津: 天津大学, 2006.
- 2. 袁春华, 王江. 神经元模型的稳定性分析与Hopf分岔控制[J]. 振动工程学报, 2015, 28(1): 52-58.
- 3. 周毅. 神经元Morris-Lecar模型簇放电活动的分岔研究[J]. 长春工业大学学报(自然科学版), 2012, 33(4): 427-431.
- 4. 杨雨潼, 刘深泉. FHN-ML电耦合神经元的发放模式和分岔分析[J]. 中国医学物理学杂志, 2017, 34(3): 306-313.
- 5. 魏春玲, 古华光, 杨明浩, 等. 周期激励下FitzHugh-Nagumo模型的两种多峰分布放电节律[J]. 生物物理学报, 2008, 24(1): 22-28.
- 6. Megam Ngouonkadi, E.B., Fotsin, H.B., Louodop Fotso, P., et al. (2016) Bifurcations and Multistablity in the Extend Hindmarsh-Rose Neuronal Oscillator. Chaos, Solitons and Fractals, 85, 151-163. https://doi.org/10.1016/j.chaos.2016.02.001
- 7. Hassard, B.D. and Wan, Y.H. (1978) Bifurcation Formulae Derived from Center Manifold Theory. Journal of Mathematical Analysis and Applications, 63, 297-312. https://doi.org/10.1016/0022-247X(78)90120-8