Advances in Applied Mathematics
Vol.
13
No.
03
(
2024
), Article ID:
83217
,
11
pages
10.12677/aam.2024.133093
由Lévy过程驱动的加权自排斥扩散的长时间 行为和统计推断
鲁蕴涵,闫理坦*
东华大学理学院,上海
收稿日期:2024年2月25日;录用日期:2024年3月19日;发布日期:2024年3月26日

摘要
假设
是一个跳有界且界限为1的Lévy过程,生成三元组为
。在本文中,我们考虑了由Lévy过程驱动的线性自排斥扩散方程
,其中,
和
。这类过程是一类自交互扩散过程。我们研究了当
趋于无穷时解的长时间行为,发现它具有一种循环收敛性,这在此前的研究中尚未有类似的结论。进一步的,当
时在连续观测情况下,通过最小二乘法给出了方程参数的估计。我们证明了
的估计量具有强相合性,并讨论了它的渐近分布。
关键词
Lévy过程,自排斥扩散,长时间行为,参数估计,渐近分布

Long Time Behavior and Statistical Inference of the Weighted Self-Repelling Diffusion Driven by Lévy Process
Yunhan Lu, Litan Yan*
College of Science, Donghua University, Shanghai
Received: Feb. 25th, 2024; accepted: Mar. 19th, 2024; published: Mar. 26th, 2024

ABSTRACT
Let
be a Lévy process with jumps bounded by 1 and generating triplet
. In this paper, as an attempt we consider the linear self-repelling diffusion driven by a Lévy process,
, where
and the parameter
. This process is similar to a type of self-interacting diffusion process. This paper studies the long time behaviour of the solution as t tends to infinity, and we find that it exhibits a cyclic convergence property, for which similar conclusions have not appeared in previous studies. In addition, when
, by using least squares method, we establish the strong consistency of the estimate
and discuss its asymptotic distribution under the consecutive observation.
Keywords:Lévy Process, The Self-Repelling Diffusion, Long Time Behaviour, Parameter Estimation, Asymptotic Distribution

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1995年,Cranston和Le Jan [1] 介绍了一种特殊随机微分方程( 即线性自吸引扩散)
(1)
其中
和
,B是一个一维标准布朗运动。他们证明了当t趋于无穷时解的收敛性。这种路径依赖随机微分方程是由Durrett和Rogers [2] 首次提出,他们在1992年引入一类增长物模型
其中B是一个d-维标准布朗运动,函数f是Lipschitz连续的。
对应于t时刻聚合物末端的位置。在一定条件下,他们建立了随机微分方程解的渐近性态,并给出了一些猜想和问题。我们把这个解称为布朗运动与它自身通过的轨迹相互作用,即自交互作用的运动。一般来说,如果对f没有任何限制,方程(1)定义了一个自交互扩散。对任意
,若
(反之
),我们称之为自排斥扩散(反之,自吸引扩散)。换句话说,它更倾向于远离(或回到)之前达到的位置。更多相关结果可参考文献 [3] - [13] 及其参考文献。值得注意的是,自交互扩散与O-U过程相当。因此,我们可以得到它的渐近行为。自交互扩散也可以用来描述经济学中空间垄断竞争的一些行为。然而,目前研究的大多数方程都是由布朗运动驱动的。自然而然地,我们可以考虑由Lévy过程或高斯过程驱动的随机微分方程。通过分部积分,方程(1)可以改写为
受此结果的启发,可以考虑方程
在本文中我们考虑
(2)
其中,
和
是
上跳有界且界为1的Lévy过程。记
。在第二章中,我们简要回顾Lévy过程的一些概念。第三章中设
,我们证明了当t趋于无穷时,有
以及
在
和几乎处处意义上存在,其中
,
。这种循环收敛性是非常难得的。在此之前,对于由此类Lévy过程驱动的随机微分方程的研究非常有限,也没有出现类似关于解的循环收敛性的结论。第四章中,当
时,在连续观测下我们估计了方程 的参数
,得到了估计量
具有强相合性且当T趋于无穷大时,以下依分布收敛性成立:
其中
为一无限可分分布,并且
和
相互独立。
2. 预备知识
在本小节中,我们简要回顾
上Lévy过程的定义和性质。关于这些概念的背景,我们参考Applebaum [14] 和Sato [15] 。在本文中,我们考虑定义在概率空间
上的Lévy过程。为简单起见,我们让C代表一个正常数,仅取决于下标,其值在不同的情况下可能会有所不同。
定义在概率空间
上的随机过程
,如果它满足:
1)
a.s;
2) L有独立、平稳增量;
3) L是随机连续的,即对任意
,
我们称之为Lévy过程。定义在
上的Lévy过程
是半鞅,有如下Lévy-Itô分解:
(3)
其中,
,
是一布朗运动,N是
上一独立泊松测度。若定义在
上的Lévy过程
跳有界,那么对一切正整数m,有
此时,过程
是鞅过程。本文中,我们假设
是一个跳有界且界限为1的Lévy过程,其生成三元组为
,由(3)我们有
对上述Lévy过程
,下方不等式成立:
和
其中
,
为停时,
是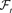 -适应过程。
-适应过程。
3. 自排斥条件下解的长时间行为
在本章中,我们考虑自排斥情况下的方程(2)。不难证明方程(2)有唯一解(参见Protter [16] )。定义核函数
其中
,并且对一切
,极限
存在。通过常数变易法,我们得到方程(2)的解
我们引入如下引理。
引理3.1 设
,定义函数
考虑函数列
,有如下形式:
其中
。那么,对
,
(4)
证明:仿照文献 [11] 的方法,对
进行
次分部积分,那么对任意
,当t趋于无穷时有
其中
结合
的定义,对任意整数
,有
和
又因为对于任意的整数
,当t趋于无穷时,
所以有
也就表明收敛性(4)成立。
引理3.2 设
,定义函数
过程
和随机变量
在
上是适定的。当t趋于无穷时,
(5)
在
和几乎处处意义下成立,其中
和
。
证明 给定
,记
。对
,有
此外,当t趋于无穷时,基于
以及
我们得到收敛性(5)在
上成立。现证明它依概率1收敛。对任意
,当t趋于无穷时,
几乎处处成立。进一步地,当t趋于无穷时,
我们得到了引理。
引理3.3 假设
,函数
为引理3.1中定义得函数,则
和
证明 给定
,利用洛必达法则,可以得到
当
时,显然
令
其中
,则对任意的
,显然有
和
另一方面,对任意的
,当t趋于无穷时,有
和
成立。则
由洛必达法则得,
证毕。
引理3.4 假设
,
为引理3.1中所定义函数,则随机变量
在
意义下存在并且
在
和几乎处处意义下成立。
证明 给定
,对一切
,有
。由引理3.3得,对任意的
,下列连续性成立:
(6)
(7)
显然当
时有
我们考虑当t趋于无穷时,
的收敛性。记
当t趋于无穷时,由(6)我们有
接下来,我们证明对一切
,当t趋于无穷时
几乎处处收敛到零。当t趋于无穷时,通过(6)、(7)和分部积分,显然有
几乎处处成立,引理得证。
定理3.5 假设
。当
时,
在
和几乎处处意义下收敛。
证明 给定
。当
时有
通过分部积分,有
又因为对任意
,
所以有
(8)
因此,当t趋于无穷时,由事实
在
和几乎处处意义下成立以及引理3.1、引理3.2和引理3.4可得,
在
和几乎处处意义下成立。
定理3.6 假设
。定义递推过程
,即,
则对任意
,当t趋于无穷时,
在
和几乎处处意义下成立,其中
是方程(2)的解且
。
证明 给定
。当
时,(8)表明对任意
和
,
其中
是引理3.1中定义的。因此,该定理的证明可以由(4)、(5)和引理3.4得到。
4. 统计推断
在本章中,我们研究微分方程
在连续观测下的参数估计。记
。
的最小二乘估计量可由以下比较函数的最小值求出:
得到
的最小二乘估计量
由常数变易法得
(9)
为了研究参数的相合性和渐近分布,我们引入了一个引理。
引理4.1 当T趋于无穷时,有如下依分布收敛成立:
其中随机变量
服从三元组
的无限可分分布,
。
证明 显然,对任意
,有
其中
服从一个无限可分分布,生成三元组为
。这里等号“=”表示分布相等。我们知道
的特征函数如下:
记
于是我们可以得到
故我们得到了
以及
引理得证。
定理4.1 假设
,则估计量
是强相合的,换句话说,当T趋于无穷时,
几乎必然成立。进一步地,当T趋于无穷大时,以下依分布收敛性成立:
其中
如引理4.1中所定义,并且
和
相互独立。
证明 由分部积分可得
结合(9)、引理3.2和洛必达法则,可以证明当T趋于无穷大时,以下收敛以概率1成立:
此外,当T趋于无穷大时有
综合以上结论,我们可以得到:
几乎必然成立。接下来我们考虑估计量
的渐近分布。对任意
,我们有
记
,对任意
,有
当T趋于无穷时,由
可以得到
综上所述结合引理4.1,有
依分布收敛,其中
服从无限可分分布,生成三元组为
并且
和
相互独立。定理得证。
文章引用
鲁蕴涵,闫理坦. 由Lévy过程驱动的加权自排斥扩散的长时间行为和统计推断
Long Time Behavior and Statistical Inference of the Weighted Self-Repelling Diffusion Driven by Lévy Process[J]. 应用数学进展, 2024, 13(03): 991-1001. https://doi.org/10.12677/aam.2024.133093
参考文献
- 1. Cranston, M. and Le Jan, Y. (1995) Self-Attracting Diffusion: Two Case Studies. MathematischeAnnalen, 303, 87-93. https://doi.org/10.1007/BF01460980
- 2. Durrett, R. and Rogers, L.C.G. (1992) Asymptotic Behavior of Brownian Polymer. Probability Theory and Related Fields, 92, 337-349. https://doi.org/10.1007/BF01300560
- 3. Benaïm, M., Ciotir, I. and Gauthier, C.-E. (2015) Self-Repelling Diffusions via an Infinite Dimensional Approach. Stochastic Partial Differential Equations: Analysis and Computations, 3, 506-530. https://doi.org/10.1007/s40072-015-0059-5
- 4. Benaïm, M., Ledoux, M. and Raimond, O. (2002) Self-Interacting Diffusions. Probability Theory and Related Fields, 122, 1-41. https://doi.org/10.1007/s004400100161
- 5. Cranston, M. and Mountford, T.S. (1996) The Strong Law of Large Numbers for a Brownian Polymer. Annals of Probability, 24, 1300-1323. https://doi.org/10.1214/aop/1065725183
- 6. Gauthier, C.-E. (2016) Self Attracting Diffusions on a Sphere and Application to a Periodic Case. Electronic Communications in Probability, 21, 1-12. https://doi.org/10.1214/16-ECP4547
- 7. Herrmann, S. and Roynette, B. (2003) Boundedness and Convergence of Some Self-Attracting Diffusions. MathematischeAnnalen, 325, 81-96. https://doi.org/10.1007/s00208-002-0370-0
- 8. Herrmann, S. and Scheutzow, M. (2004) Rate of Convergence of Some Self-Attracting Diffusions. Stochastic Processes and Their Applications, 111, 41-55. https://doi.org/10.1016/j.spa.2003.10.012
- 9. Kleptsyny , V. and Kurtzmann, A. (2012) Ergodicity of Self-Attracting Motion. Electronic Journal of Probability, 17, 1-37. https://doi.org/10.1214/EJP.v17-2121
- 10. Mountford, T. and Tarrès, P. (2008) An Asymptotic Result for Brownian Polymers. Annales de l’IHPProbabilités et Statistiques, 44, 29-46. https://doi.org/10.1214/07-AIHP113
- 11. Sun, X. and Yan, L. (2021) Asymptotic Behaviour on the Linear Self-Interacting Diffusion Driven by ɑ-Stable Motion. Stochastics: An International Journal of Probability and Stochastic Processes, 93, 1186-1208. https://doi.org/10.1080/17442508.2020.1869239
- 12. Sun, X. and Yan, L. (2022) The Laws of Large Numbers Associated with the Linear Self-Attracting Diffusion Driven by Fractional Brownian Motion and Applications. Journal of Theoretical Probability, 35, 1423-1478. https://doi.org/10.1007/s10959-021-01126-0
- 13. Yan, L., Sun, Y. and Lu, Y. (2008) On the Linear Fractional Self-Attracting Diffusion. Journal of Theoretical Probability, 21, 502-516. https://doi.org/10.1007/s10959-007-0113-y
- 14. Applebaum, D. (2004) Lévy Processes and Stochastic Calculus. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511755323
- 15. Sato, K. (1999) Lévy Processes and Infinite Divisibility. Cambridge University Press, Cambridge.
- 16. Protter, P. (2005) Stochastic Integration and Differential Equations. Vol. 21, Springer, Berlin, Heidelberg and New York. https://doi.org/10.1007/978-3-662-10061-5_6
NOTES
*通讯作者。






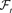 -适应过程。
-适应过程。