Journal of Image and Signal Processing
Vol.
08
No.
03
(
2019
), Article ID:
31517
,
14
pages
10.12677/JISP.2019.83024
New Template Matching Method for Subpixel Mapping of Linear Feature Mixed Pixels
Haiqiang Lu1, Zhaoxin Liu2*, Wei Zhu1
1Hengchuang Power Equipment Co., Ltd., Jiaxing Zhejiang
2College of Computer Science, Hangzhou Dianzi University, Hangzhou Zhejiang

Received: Jul. 4th, 2019; accepted: Jul. 22nd, 2019; published: Jul. 29th, 2019

ABSTRACT
By analyzing the problems of subpixel mapping algorithm based on template matching, a linear feature sub-pixel mapping algorithm based on improved template matching is proposed. Based on the correlation coefficient selection template, two new template selection methods are proposed: 1) Further determining the template by fitting a line with linear feature mixed pixels eight neighborhood, to some extent, reduces the scope of template selection; 2) In order to avoid the uncertainty of template selection, the best template is obtained through line fitting on the mixed pixels eight neighborhoods and the template and calculating the linear correlation. Furthermore, combined with pixel gravity, the sub-pixel mapping problem of linear feature pixel containing three or more ground objects is solved. The experiment results show that the proposed method can improve the sub-pixel mapping accuracy.
Keywords:Mixed Pixel, Subpixel Mapping, Template Matching, Correlation Coefficient, Line Fitting
一种基于模板匹配的线性特征混合像元的 亚像元定位的新方法
陆海强1,刘照欣2*,朱伟1
1嘉兴市恒创电力设备有限公司,浙江 嘉兴
2杭州电子科技大学计算机学院,浙江 杭州

收稿日期:2019年7月4日;录用日期:2019年7月22日;发布日期:2019年7月29日

摘 要
通过分析基于模板匹配的含线特征混合像元亚像元定位算法存在的问题,提出改进的模板匹配新方法。在相关系数选择模板的基础上提出两种新的模板选择方法:1) 对含线特征混合像元八邻域拟合直线进一步确定模板,在一定程度上缩小了模板选择的范围;2) 为避免模板选择的不确定性,对含线特征混合像元八邻域及模板分别进行直线拟合,计算直线相关性,得出最佳模板。进一步地,结合像元引力解决包含三种及以上地物混合的含线特征像元的亚像元定位问题。实验结果表明所提出的方法能提高亚像元定位精度。
关键词 :混合像元,亚像元定位,模板匹配,相关系数,直线拟合

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着遥感技术的发展,遥感图像已被广泛的应用到地质学、海洋学、农业/植被规划和生态环境监测等。由于传感器空间分辨率的限制以及地物空间的复杂多样性,混合像元普遍存在于遥感影像中,如何准确的获取地表覆盖信息在诸多遥感应用方面都有着及其重要的意义 [1] [2] 。软分类技术,能够获取像元中每一个地物类别对应的丰度,获得与类别个数相等的丰度影像,有效的解决混合像元问题,但无法确定各种地物在像元空间中的具体位置 [3] [4] 。Atkinson [5] 首次提出了亚像元定位(subpixel mapping, SPM)的概念。
亚像元定位主要思想是将混合像元按需求放大比例进行分割,确定每个亚像元的所属类别即确定混合像元中不同地物类型具体空间分布。目前主要的亚像元定位算法主要有像元交换 [6],亚像元/像元空间引力 [7],神经网络 [8] [9],软硬属性转换 [10] [11],线性优化 [12] [13] [14] 等模型。上述方法都忽略了混合像元内部不同的结构特征。针对该问题,国内学者许雄提出了顾忌地物空间分布的亚像元定位方法 [15],将混合像元分为边界混合像元和线特征混合像元,利用特征探测、定位和决策等多个智能体分别实现不同特征的获取、不同特征的定位和最后的优化处理;葛勇等通过形状密度指数将地物目标分为点、线、面三类,针对不同的目标使用相应的定位方法 [16] 。对含线特征的混合像元内的亚像元定位用了模板匹配方法,但是该方法无法解决多个模板中如何智能选取最优模板问题,为此本文提出两种模板选择方法,实验证明所提出的模板选择方案能有效解决模板选择时多个模板最优问题。通过分析基于模板匹配的亚像元定位算法存在的问题,提出了基于改进模板匹配的线特征亚像元定位算法。
2. 含线特征混合像元亚像元定位的模板匹配法
2.1. 含线特征混合像元
由于传感器空间分辨率的限制和地物的复杂多样性,遥感图像中混合像元普遍存在。Fisher等 [17] 将遥感图像中混合像元划分为四种类型:亚像元目标、边界混合像元、致密型混合像元和线性目标,如图1所示,其中每个小方格表示1个像元,不同的颜色表示混合像元内不同的地物及其不同类型的空间分布。如图1(d)所示的线性目标对应的混合像元称为含线特征混合像元,该类混合像元一般为某类线性地物,如道路、河流等,由于其宽度和长度分别小于和大于影像空间分辨率,从而造成其贯穿多个混合像元造成的。
每种地物在一个混合像元内占的面积百比分称为该地物在该混合像元内的丰度。
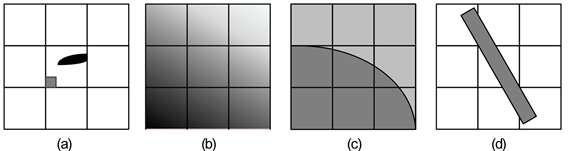
Figure 1. Four different types of mixed pixels. (a) Sub-pixel target; (b) Dense mixed pixels; (c) Boundary mixed pixel; (d) Linear target
图1. 混和像元的四种不同类型。(a) 亚像元目标;(b) 致密型混合像元;(c) 边界混合像元;(d) 线性目标
2.2. 亚像元定位的模板匹配法
基于模板匹配的线状地物亚像元定位方法基本原理包括以下3个步骤 [16] :
1) 对每个混合像元,确定像元尺度下最佳匹配的线状模板。

Figure 2. 3 × 3 template
图2. 3 × 3模板
以图2所示的3 × 3的线状模板为例,每个模板可用二进制矩阵表示为:
(1)
其中,矩阵各元素 , 表示对应图1中的灰色小方格, 对应图1中的白色方格。同理,可以构建重建尺度为 的二进制模板矩阵。
根据各模板和以混合像元Pij为中心的 邻域各像元中线状分布地物的丰度之间的匹配程度确定Pij的最佳匹配模板。匹配程度的度量方法有多种 [17] 。以标准相关匹配(Standard correlation, SC)方法为例,对混合像元中呈线性分布的第c类地物进行亚像元定位。设 ,计算图2中各模板和以混合像元Pij为中心的 邻域各像元第c类地物丰度之间的相关系数
(2)
其中, 表示模板矩阵中第k个模板 位置的元素值, 表示图像中第c类地物的丰度值。
由式(1)可知,ri,j,k的取值范围在0~1之间,值越接近1模板的匹配效果越好,反之效果越差。对图2中的所有模板依次计算相关系数,取值最大的模板为最佳模板。
2) 利用最优模板 对混合像元Pij中第c类地物进行定位。
根据丰度求得第c类地物在混合像元Pij内所占的亚像元个数 ,建立像元和亚像元的统一坐标系 [17],在统一坐标系中,计算亚像元vpq与最优模板 中各元素之间的欧式距离,离模板距离最小的 个亚像元类别为c。
3) 像元内其他亚像元类别确定
分别计算像元内其他地物的亚像元个数,随机确定像元内剩余亚像元的类别。
2.3. 存在的问题
上述模板匹配亚像元定位方法存在如下问题:
1) 直接根据相关系数ri,j,k进行模板选择时最大ri,j,k对应的模板可能不唯一,如何从多个匹配的模板中选出唯一的最优模板仍是个问题;
2) 当混合像元内包含三种及以上地物时,用随机方法确定像元内其他亚像元类别不够准确。
3. 两种最佳匹配模板确定的新方法
针对问题1)提出标准相关匹配结合像元直线拟合(Pixel Line Fitting after Standard Correlation, SC-PLF)的方法,标准相关匹配结合直线拟合相关性(Line Fitting Correlation after Standard Correlation, SC-LFC)的方法。
3.1. 基于拟合直线的最佳匹配模板确定
根据混合像元Pij及其八邻域中地物 的丰度值进行二值化,即8邻域中如果含有第c类地物则将该混合像元标记为1,否则标记为0。图3(a)为第c类地物8邻域丰度示意图,图3(b)中0~1值表示二值化操作后的结果。求出二值化后八邻域中值为1的像元中心坐标,基于线性最小二乘法拟合直线,如图3(b)所示。

Figure 3. Schematic diagram of line fitting. (a) Eight neighborhood abundance map of mixed pixels of class c; (b) Linear fitting after binarization
图3. 直线拟合示意图。(a) 混合像元第c类地物八邻域丰度图;(b) 二值化后直线拟合
以重建尺度 为例说明像元中心坐标的表示。将混合像元Pij及其8邻域放在同一坐标系并以左上角为坐标原点,如图3(b)所示,以左上角为统一坐标系原点,将每一个小方格长度记为1,因此在该同一坐标系中,左上角的亚像元 坐标为(0.5, 0.5),左上角像元 坐标为(2, 2),像元 的坐标为 ,亚像元 的坐标为 。

Figure 4. 4 results of line fitting
图4. 4种直线拟合结果
对于SC确定的若干模板,依次判断模板矩阵中值为1的像元是否被拟合后的直线所经过,并统计其个数NT。设拟合直线La的方程为 ,模板矩阵中值为1的像元 中心坐标为 ,则像元Pmn到直线La的距离为
(3)
如果 ,则像元Pmn被直线La经过。
NT值最大的模板为最优模板。图4给出了图2中部分模板的直线拟合结果,其中各模板中直线所经过的灰色区域个数NT分别为1,3,2,1,图4(b)所示模板为最优模板。
3.2. 标准相关匹配结合直线拟合相关性选择最佳模板
SC-PLF方法虽然进一步缩小了模板选择的范围,但是对于模板唯一性仍无法保证。为此本节提出了标准相关匹配结合直线拟合相关性(Line Fitting Correlation after Standard Correlation, SC-LFC)的方法,在基于标准相关性的模板匹配选择方法选择出的若干模板基础上,分别对所选的模板和含线特征混合像元邻域进行直线拟合,并计算各模板和像元拟合直线间的相关性,可以保证模板选择的唯一性,算法主要思想是:
1) 对混合像元Pi,j及其邻域像元根据地物 的丰度进行二值化,拟合直线 ;
2) 对经过SC算法选择出的各模板,根据 的位置拟合直线 ;
3) 利用式(4)计算La和直线 的相关性:
(4)
其中,w1和w2为权重,k1和 分别为直线La和直线Li的斜率,同理,b1和bi则为直线La和直线Li的截距。实验证明 , 时,所选模板能够保证唯一且最优。
图5给出了部分模板的拟合直线结果,LCi的值越大说明相关性越大。因此通过选择LCi最大值对应的模板得出最优结果。

Figure 5. Result of line fitting
图5. 直线拟合结果
4. 改进的含线特征混合像元亚像元定位流程
针对传统模板匹配方法存在的第2个问题,提出以下改进策略:如果混合像元Pij内仅包含两种地物,则Pij内其他亚像元Pab类别可以直接确定;如果混合像元Pij内地物类别大于两类,则提出基于像元引力确定其类别。采用环绕关系确定亚像元Pab的邻域像元集 [6] :
(5)
第c类地物对亚像元Pab的引力为:
(6)
(7)
其中 为亚像元Pab的类别。
图6给出了改进的含线特征混合像元亚像元定位(Modified subpixel mapping of linear feature mixed pixels, MSPML)流程图。
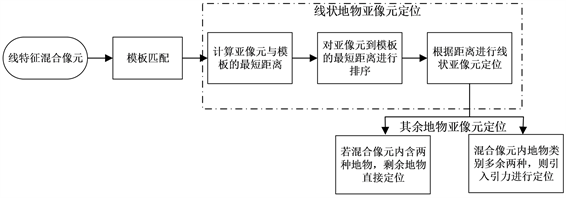
Figure 6. Schematic diagram of the subpixels mapping process of linear feature mixed pixels
图6. 含线特征混合像元亚像元定位过程示意图
5. 实验与分析
为了验证本文提出的混合像元线特征定位算法的有效性,对本章所提出的各种混合像元线特征定位方法与文献 [16] 的混合像元线特征定位方法(SPML-SC)进行实验比较。表1给出了各种算法说明。其中,SPML-SC算法的基本思想是根据区域生长法分割图像,根据面积形状指数将混合像元分为含面、线和点特征的三类,每类用不同的亚像元定位模型,其中线特征定位用SC模板匹配方法。SPML-SC的具体过程参见文献 [16],MSPML为图6所示的算法。
Table 1. Description of the subpixel mapping algorithm of linear feature mixed pixels
表1. 含线特征混合像元亚像元定位算法说明
所有的实验中,均根据文献 [18] 方法确定地物种类数,全约束最小乘法 [19] 求得丰度,采用PCA方法去噪,并使用FNSGA(Fast New Simplex Growing Algorithm)方法 [20] 提取光谱曲线。实验环境为Intel(R) CoreTM i5-3210M CPU使用的MATLAB版本为MATLAB R2014a。
5.1. 实验数据
5.1.1. 仿真数据
从USGS光谱库中选7种地物光谱按照真实地物分布生成仿真的高光谱图像,如图7(b)所示,按照3 × 3和5 × 5比例均值滤波,构造相应的混合像元丰度,得到如图7(c)和图7(d)所示的高光谱图像(第40波段)。
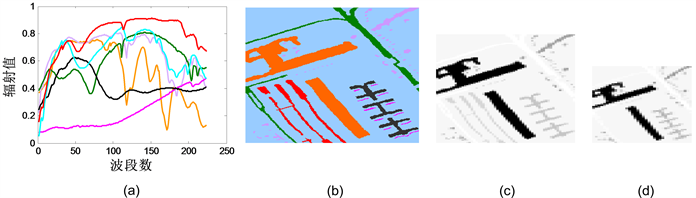
Figure 7. Synthetic dataset. (a) 7 kinds of ground spectrum; (b) Ground truth; (c) 90 × 60 synthetic map; (d) 54 × 36 synthetic map
图7. 仿真数据。(a) 7种地物光谱曲线;(b) 真实地物分布图;(c) 90 × 60仿真图;(d) 54 × 36仿真图
5.1.2. 真实数据
采集意大利北部帕维亚大学的ROSIS高光谱遥感影像,截取117 × 75大小的区域,该区域共包含5类地物,其真实地物分布如图8(b)所示,3 × 3均值滤波,图8(a)为滤波后第37波段的灰度图,用VCA + FCLS得到丰度图像。同文献 [21],对丰度进行调整,将最大丰度值与其他丰度值之差的最小值大于某个阈值的像素作为纯像元,因为金属区域比较明显,只统计金属区域的定位识别率,通过实验发现阈值取0.4。

Figure 8. Real hyperspectral dataset. (a) Grayscale map of the 37th band; (b) Ground truth
图8. 真实的高光谱图像。(a) 第37波段的灰度图;(b) 真实地物分布
5.2. 混合像元内线状地物亚像元定位实验
基于模板匹配的线特征探测方法的实验采用仿真数据进行实验验证,为便于分析,从图7(b)所示的真实地物分布中截取[245:259, 86:103]区域并放大,子图截取示意图如图9(a)所示,放大后的子图如图9(b)所示,图9(a)和图9(b)对应的线特征探测结果分别如图9(c)和图9(d)所示。由图9(c)可以看出该区域为典型的线状区域,因此截取图9(b)区域作为实验数据。图9(d)为所截取区域的线特征探测结果。实验最终评价采用主观评价和客观评价两种手段,客观评价则根据最终定位的识别率 [22] 、kappa系数 [23] 和时间效率为指标。

Figure 9. Experimental data. (a) Schematic diagram of subgraph capture; (b) Scaled subgraph; (c) Line feature detection result of graph (a); (d) Detection result of graph (b)
图9. 实验数据。(a) 子图截取示意图;(b) 放大后的子图;(c) 图(a)的线特征探测结果;(d)图(b)的探测结果
图10给出了图9(b)所示区域的线特征混合像元亚像元定位结果。为了便于对照图9(d)的线特征探测结果,图11给出了线探测结果与线特征混合像元定位叠加后的结果示意图,通过图11可以明显看到每个含线特征的混合像元内地物的具体分布情况。
根据图10和图11对线特征混合像元定位结果进行分析,可以发现图10(e)对线性体地物定位时聚集性不好,存在孤立像素点;而其他几种算法在利用模板对线特征地物进行定位时,在距离相同的情况下结合邻域像元引力进行亚像元进行定位,在一定程度上保证了线特征地物的连通性,且满足了空间相关性理论。由图10(a)可知该区域地物呈线状分布,此时通过相关系数结合直线拟合相关性进行线特征地物进行定位时效果较好,如图11(a)所示,通过图11(a)可以看出中间部分像元的定位效果明显优于其他算法,聚集性较好且不存在孤立点。对比图10(b)和图10(c~d)可以发现,图10(b)对线性体地物的定位效果优于图10(c)和图10(d),更接近原图10(a),这说明本文针对模板匹配存在的问题提出的解决方法是有效的。在该区域MSPML-SC-PLF法对线特征混合像元进行模板匹配定位时效果不明显,但与图10(e)相比,不存在孤立点。

Figure 10. Result of line feature mixed pixels mapping
图10. 线特征混合像元定位结果

Figure 11. Result of line detection (a) and result of line future mixed pixels mapping (b) - (e)
图11. 线探测结果(a)与线特征混合像元定位结果(b)~(e)
表2给出了不同算法线特征地物定位的定量化统计结果。从表2中可以看出MSPML-SC-LFC算法相比于其他算法能够取得较高的识别率及kappa系数。MSPML-SC和SPML-SC相比,由于在定位时加入邻域像元引力,导致其绿色地物聚集性更加符合最终分类效果,因此在提高识别率的同时增加了时间消耗。MSPML-SC与MSPML-SC-LFC相比识别率有所降低,这是模板选择的影响,因为后者在若干最优模板中能通过算法进行唯一且最优模板的选择。
Table 2. Comparison of mixed pixels mapping results of each line feature algorithm (without optimization)
表2. 各算法线特征混合像元定位结果比较(未优化)
为了进一步对实验结论进行验证,图12给出了图9(b)所示区域按照线面结合算法思想的亚像元定位结果。对照图12(a)进行分析可以发现图12(b)的定位效果最好,这说明改进后的模板选择算法能够有效提高模板选择及定位效果。其次本文所使用的模板匹配结合像元引力的线特征定位算法图12(c)的定位结果相比于文献 [16] 的模板匹配算法即图12(e)的定位效果更加符合地物真实的分类结果,这说明本文所提出的模板匹配结合像元引力的算法能够有效提高亚像元定位精度。

Figure 12. Result of subpixel mapping of Figure 9(b)
表3给出了不同线特征定位算法的实验数据。
Table 3. Subpixel mapping result of each algorithm
表3. 各算法亚像元定位结果
从表3中得出的数据我们可以看出MSPML-SC-LFC的识别率及kappa系数相对较高,这验证了我们对图12的分析。其次是MSPML-SC和MSPML-SC-PLF算法的识别率虽低于MSPML-SC-LFC,但高于仅根据模板进行定位的SPML-SC算法,从理论上验证本文提出的模板结合引力的算法的有效性。另外本文提出的对模板进行改进的算法MSPML-SC-LFC及MSPML-SC-PLF,无论从图12还是表3中都能看出其定位都优于文献 [16] 的模板匹配算法SPML-SC,且与MSPML-SC相比能够实现较高的识别率,虽然在模板选择时加入拟合直线对模板进行选择但其算法的时间效率并未降低。
5.3. 亚像元定位实验
在5.2不同混合像元线特征定位的基础上,对剩余面状地物进行定位,并对最终的亚像元定位结果进行迭代优化。实验需比较的算法为前述三种线特征定位分别结合线性优化的面状地物定位 [12],为便于描述分别记为MSPMLA-SC、MSPMLA-SC-PLF及MSPMLA-SC-LFC。另外还包括文献 [16] 所提出的定位算法SPMLA-SC以及基于线性优化的亚像元定位算法 [12] 记为SPMLA-LO。同时为了有效的验证实验结果的有效性,仍采用最后定位的识别率,kappa系数以及运行时间为客观评价指标。
5.3.1. 仿真数据实验
对图7(c)所示的重建尺度s = 3的仿真数据进行亚像元定位,结果如图13,从图13中红色黑色相兼的区域或正红色区域,可以看出图13(b)和图13(c)的连通性较好且定位效果较光滑,这说明改进模板选择的方法有助于提高亚像元定位精度,且图13(c)在右下角黑色和红色相兼区域的连通性优于图13(b)。对图13(e)和图13(d)的右下角红色和黑色相兼的地方进行比较可以看出图13(d)的连通性要较好,因此所提出的模板匹配结合像元引力的方法,能有效提高地物分类精度。图13(f)为传统亚像元定位算法,由于定位时未考虑线状分布地物定位问题,其连通性不如其他几种方法。

Figure 13. Subpixel mapping result of reconstruction scale of 3
图13. 重建尺度为3的亚像元定位结果
图14给出了五种算法对图7(b)的亚像元定位结果。由于重建尺度的增大使得图像中混合像元数量增多,因此图14定位结果中各算法毛刺现象严重。图14从视觉上已经很难分出哪种方法比较好,为了更加准确的验证实验效果,对算法的识别率,kappa系数及运行时间进行统计。
表4和表5分别给出了重建尺度为3和5时,各实验结果的识别率、kappa以及时间比较,为了避免例子群算法的初值敏感性对结果的影响,每组实验中各算法每次运行全部使用了同样的初始粒子群(粒子个数为30)。首先基于传统亚像元定位的SPMLA-LO无论在重建尺度为3还是5时的定位效果都不如考虑地物空间分布的亚像元定位的识别率高。对基于模板的几种算法进行比较时,MSPMLA-SC-LFC无论在重建为3还是5时都能取得相对较高的识别率,说明所提出的模板选择方法的有效性,由于在模板选择时又加入其它的条件以提高模板选择的准确性,所以其时间消耗相对较高。另外MSPMLA-SC-PLF、MSPMLA-SC-LFC和MSPMLA-SC均高于不考虑邻域像元引力的SPMLA-SC的定位精度,这说明所提出的模板选择结合邻域像元引力能够有效提高亚像元定位精度。

Figure 14. Subpixel mapping result with reconstruction scale of 5
图14. 重建尺度为5的亚像元定位结果
Table 4. Experiment result with reconstruction scale of 3
表4. 重建尺度为3时的实验结果
Table 5. Experiment result with reconstruction scale of 5
表5. 重建尺度为5时的实验结果
通过以上实验我们可以得出以下四点结论:1) 基于地物空间分布的亚像元定位算法优于传统的亚像元定位算法;2) 基于模板选择的亚像元定位算法中,所提出的几种亚像元定位方法定位效果优于SPMLA-SC,且MSPMLA-SC-LFC的定位效果最好,说明所提出的改进模板选择的算法能够有效提高亚像元定位精度;3) 从表1与表2的对比中我们可以发现,随着重建尺度的增大,纯像元锐减,导致识别率降低。
5.3.2. 真实数据实验
对图5(a)进行3 × 3滤波后的亚像元定位结果如图15所示。

Figure 15. Result of subpixel mapping
图15. 像元定位结果
表6给出了六种方法定量化的实验结果。由图15和表6分析可知基于地物空间分布的定位方式比传统的亚像元定位图15(f)精度要高;表6中SPMLA-SC的识别率虽高于传统亚像元定位算法,但由于模板选择时无法确定模板中最优模板且定位时未考虑像元引力,所以识别率仍低于本文提出的其它三种策略。识别率最高的为MSPMLA-SC-LFC算法,证明该种模板选择的方式能够有效提高亚像元定位精度,也为后续利用模板进行亚像元定位提供了参考依据。
Table 6. Experiment result with reconstruction scale of 3
表6. 尺度为3时的实验结果
6. 结论
模板匹配和直线拟合是目前常用的线特征定位算法。由于模板匹配算法提高亚像元空间分辨率主要依赖于模板选择,仅采用标准相关系数(SC)对模板进行选择并不能保证所选模板最优,即存在最优模板存在多个的情况。本文针对基于模板选择部分提出两种模板选择方案,分别为SC-PLF和SC-LFC。其次,为进一步对混合像元内其余地物更好地定位,可采用模板匹配结合像元引力的方法,实验证明所提出的基于模板匹配的含线特征混合像元定位方法不仅能保证线特征的连通性而且使得混合像元内其余地物在定位时更加符合空间相关性。
基金项目
国家自然科学基金(No.61671408, No.61571170);教育部联合基金(No.6141A02022350);企业重大合作项目(No. KM20180179)。
文章引用
陆海强,刘照欣,朱 伟. 一种基于模板匹配的线性特征混合像元的亚像元定位的新方法
New Template Matching Method for Subpixel Mapping of Linear Feature Mixed Pixels[J]. 图像与信号处理, 2019, 08(03): 180-193. https://doi.org/10.12677/JISP.2019.83024
参考文献
- 1. Tong, X., Xu, X., Plaza, A., et al. (2016) A New Genetic Method for Subpixel Mapping Using Hyperspectral Images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 9, 4480-4491.
https://doi.org/10.1109/JSTARS.2015.2496660 - 2. Bioucas-Dias, J.M., Plaza, A., et al. (2012) Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2, 354-379.
https://doi.org/10.1109/JSTARS.2012.2194696 - 3. 陈晋, 马磊, 陈学泓. 混合像元分解技术及其进展[J]. 遥感学报, 2016, 20(5): 1102-1109.
- 4. 赵春晖, 成宝芝, 杨伟超. 利用约束非负矩阵分解的高光谱解混算法[J]. 哈尔滨工程大学学报, 2012, 33(3): 377-382.
- 5. Athinkson, P.M. (1997) Mapping Sub-Pixel Boundaries from Remotely Sensed Images. Innovations in GIS, 4, 166-180.
- 6. Xu, X., Zhong, Y. and Zhang, L. (2014) A Sub-Pixel Mapping Method Based on an Attraction Model for Multiple Shifted Remotely Sensed Images. Neurocomputing, 134, 79-91.
https://doi.org/10.1016/j.neucom.2012.12.078 - 7. Wu, S., Chen, Z., Ren, J., et al. (2018) An Improved Subpixel Mapping Algorithm Based on a Combination of the Spatial Attraction and Pixel Swapping Models for Multispectral Remote Sensing Imagery. IEEE Geoscience and Remote Sensing Letters, 15, 1-5.
https://doi.org/10.1109/LGRS.2018.2825472 - 8. 许雄, 钟燕飞, 张良培, 等. 基于空间自相关BP神经网络的遥感影像亚像元定位[J]. 测绘学报, 2011, 40(3): 307-311.
- 9. 吴柯, 牛瑞卿, 沈焕峰, 等. 结合超分辨率重建的神经网络亚像元定位方法[J]. 中国图象图形学报, 2010, 15(11): 1681-1687.
- 10. 王群明. 基于软硬属性转换的遥感图像亚像元定位算法[J]. 测绘学报, 2016, 45(4): 503-503.
- 11. Wang, P., Wang, L. and Chanussot, J. (2016) Soft-then-Hard Subpixel Land Cover Mapping Based on Spatial-Spectral Interpolation. IEEE Geoscience and Remote Sensing Letters, 13, 1851:1854.
https://doi.org/10.1109/LGRS.2016.2614810 - 12. 赵辽英, 范明阳, 厉小润, 等. 基于目标优化的高光谱图像亚像元定位[J]. 中国图象图形学报, 2016, 21(6): 823-833.
- 13. Chen, S., Li, X. and Zhao, L. (2017) Subpixel Mapping Method of Hyperspec-tral Images Based on Modified Binary Quantum Particle Swarm Optimization. Journal of Electrical and Computer Engineering, No. 3, 1-17.
https://doi.org/10.1155/2017/2683248 - 14. Zhong, Y. and Zhang, L. (2013) Sub-Pixel Mapping Based on Artificial Immune Systems for Remote Sensing Imagery. Pattern Recognition, 46, 2902-2926.
https://doi.org/10.1016/j.patcog.2013.04.009 - 15. Xu, X., Zhong, Y. and Zhang, L. (2013) Adaptive Subpixel Mapping Based on a Multiagent System for Remote-Sensing Imagery. IEEE Transactions on Geoscience and Remote Sensing, 52, 787-804.
https://doi.org/10.1109/TGRS.2013.2244095 - 16. Ge, Y., Chen, Y., Stein, A., et al. (2016) Enhanced Subpixel Mapping with Spatial Distribution Patterns of Geographical Objects. IEEE Transactions on Geoscience and Remote Sensing, 54, 2356-2370.
https://doi.org/10.1109/TGRS.2015.2499790 - 17. Fisher, P. (1997) The Pixel: A Snare and a Delusion. International Journal of Remote Sensing, 18, 679-685.
https://doi.org/10.1080/014311697219015 - 18. Chang, C.I. (2017) Adaptive Linear Spectral Mixture Analysis. IEEE Transac-tions on Geoscience and Remote Sensing, 55, 1240-1253.
https://doi.org/10.1109/TGRS.2016.2620494 - 19. Heinz, D.C. and Chang, C.I. (2002) Fully Constrained Least Squares Linear Spectral Mixture Analysis Method for Material Quantification in Hyper-spectral Imagery. IEEE Transactions on Geoscience and Remote Sensing, 39, 529-545.
https://doi.org/10.1109/36.911111 - 20. 王丽姣, 厉小润, 赵辽英. 快速实现基于单形体体积生长的端元提取算法[J]. 光学学报, 2014, 34(11): 308-314.
- 21. Erturk, A., Gullu, M.K., Cesmeci, D., et al. (2014) Spatial Resolution Enhancement of Hyper-spectral Images Using Unmixing and Binary Particle Swarm Optimization. IEEE Geoscience and Remote Sensing Letter, 11, 2100-2104.
https://doi.org/10.1109/LGRS.2014.2320135 - 22. Ling, F. and Fu, B. (2009) Super-Resolution Mapping of Urban Buildings with Remotely Sensed Imagery Based on Prior Shape Information. Joint Urban Remote Sensing Event, Shanghai, 20-22 May 2009, 1-5.
https://doi.org/10.1109/URS.2009.5137529 - 23. Rwanga, S.S. and Ndambuki, J.M. (2017) Accuracy Assessment of Land Use/Land Cover Classification Using Remote Sensing and GIS. International Journal of Geosciences, 8, 611-622.
https://doi.org/10.4236/ijg.2017.84033
NOTES
*通讯作者。
