International Journal of Fluid Dynamics
Vol.
06
No.
04
(
2018
), Article ID:
28077
,
7
pages
10.12677/IJFD.2018.64018
Collision Rules and Digital Circuit Implementation of the FHP-II Lattice Gas Automata in Fluid Mechanics
Ting Li1,2, Boyu Wang1, Jianhua Chen1, Guangwu Yan1*
1College of Mathematics, Jilin University, Changchun Jilin
2College of Science, Jilin Institute of Chemical Technology, Jilin Jilin

Received: Nov. 23rd, 2018; accepted: Dec. 11th, 2018; published: Dec. 18th, 2018

ABSTRACT
In this paper, a digital circuit for simulating the evolution rules of the FHP-II lattice gas automaton model for incompressible flow is presented. Using this circuit, the Look-Up table of FHP-II is generated. As an example, we simulate the square cavity flow with small Reynolds number. The classical numerical results are reproduced.
Keywords:Lattice Gas Automata, FHP-II Model, Look-Up Table, Digital Circuit
用于流体力学的FHP-II格子气自动机的碰撞规则数字电路实现
李婷1,2,王博宇1,陈建华1,闫广武1*
1吉林大学数学学院,吉林 长春
2吉林化工学院理学院,吉林 吉林

收稿日期:2018年11月23日;录用日期:2018年12月11日;发布日期:2018年12月18日

摘 要
本文给出了用于模拟不可压缩流动的FHP-II格子气自动机模型中演化规则的数字电路。利用这个电路,生成了FHP-II的Look-Up表。作为算例,我们模拟了小雷诺数的方腔流动,再现了经典的数值结果。
关键词 :格子气自动机,FHP-II模型,Look-Up表,数字电路

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
上个世纪80年代出现的格子气自动机(Lattice Gas Automata,简记LGA)是模拟流体力学一种方法,由于其无舍入误差和运行速度快等优点受到学术界广泛关注 [1] [2]。Frisch等人应用正六边形网格,构造了包含静止粒子的满足泡利不相容原理的格子气自动机,解决了四阶张量各项同性问题,得到了低雷诺数限制的Navier-Stokes方程,该模型被称为FHP-II模型 [1]。随后的d’Humières,Lallemand和Frisch引入了四维的超四面体FCHC网格将FHP模型推广到了三维问题上 [3]。应用LGA,研究者们已经成功地模拟了许多流动,例如:卡门涡街 [4] 、磁流体力学 [5] [6] 、反应扩散模型 [7] 、Kelvin不稳定 [8]。
格子气自动机的运算是通过对每点的输入状态进行翻转实现的,翻转规则又称演化规则。根据演化规则将所有的输入状态翻转成输出状态,这个二维关系称为Look-Up表 [8] [9]。这样LGA的运算速度很大程度取决于Look-Up表的查找速度。文 [9] [10] 给出了Look-Up表状态编码的抽取和合成方法,并且用这样的Look-Up表实现了几种流动的模拟。到了21世纪,量子格子气自动机应运而生。量子格子气是基于传统格子气的设计思想,将Look-Up表进行量子实现,预期能使数据的处理和计算速度得到大幅度的提升。由此可见,Look-Up表是格子气自动机乃至量子格子气自动机的重要组成部分,而Look-Up表的数字逻辑电路的研究是硬件的基础。本文以FHP-II格子气自动机为例,给出了其Look-Up表的逻辑电路,并用这个电路验证了Look-Up表的正确性,进一步,我们用这样的结果模拟了小雷诺数的方腔流动。
2. FHP-II格子气自动机的演化规则
2.1. FHP-II碰撞规则
我们将二维空间离散成正六边形的网格,每个节点有6个邻点,假设粒子满足泡利不相容原理,则每个节点上的状态变量 是一个Boolean量,当 方向存在粒子时 ,否则为零。其中 表示节点坐标, 代表粒子运动的7个方向(静止状态也表示为一个方向,取 ),这7个运动方向的定义如图1。
FHP-II格子气自动机共提供4类碰撞规则,这些规则满足粒子守恒和动量守恒。基于流体介质的各项同行要求,碰撞是满足旋转对称的,这样一共有17种具体的规则 [9] [10]。
1) 两个粒子对头碰撞,1、4方向碰撞,输出为3、6方向,或者2、5方向。通过旋转,这种对头碰撞有3种情况。
2) 一运动粒子与一静止粒子碰撞,1、7碰撞,输出为2、5方向,这种有6种情况。
3) 两粒子120度输入,得到一静止粒子和第三个方向,即2、6方向碰撞输出为1、7方向,共6种情况。
4) 夹角120度的三粒子碰撞,即1、3、5,碰撞输出为2、4、6方向,共2种情况。
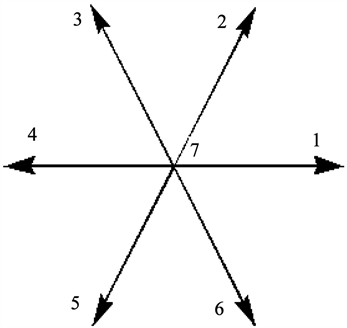
Figure 1. Schematic diagram of node orientation
图1. 节点方向示意图
2.2. Boolean动力学方程
上面的FHP-II格子气自动机的碰撞规则,可以用Boolean动力学方程描述 [11] :
其中, , ,同理可得类似的 的Boolean动力学方程。上述方程中的运算均为逻辑运算,式子中的 表示发生概率。我们将输入状态排列成7位的二进制数,其对应的整
数称为状态数。同样输出状态也可以表示成状态数。这样,在任何一个输入便得到输出,根据上面的演化规则,以及Boolean动力学方程,可得到输入输出的二维关系表,即Look-Up表。表1给出了FHP-II模型的Look-Up表。图2中,我们给出了发生碰撞的输入输出的状态分布。可以发现,大多数的输入数与输出数相同,这表示只有17个情况发生碰撞,与前文2.1部分的理论结果一致。
Table 1. Look-Up table of FHP-II lattice gas automata
表1. FHP-II格子气自动机的Look-Up表

Figure 2. Figure of relation between input number and output number
图2. 输入数与输出数的关系图
2.3. FHP-II碰撞规则的数字逻辑电路
图3中分别给出了输出
,其中符号 表示与门电路,符号
表示与门电路,符号 表示非门电路,符号
表示非门电路,符号 表示或门电路,符号
表示或门电路,符号 表示异或门电路,符号
表示异或门电路,符号 表示在两个输入端中随机取其中一个的判断器。
表示在两个输入端中随机取其中一个的判断器。
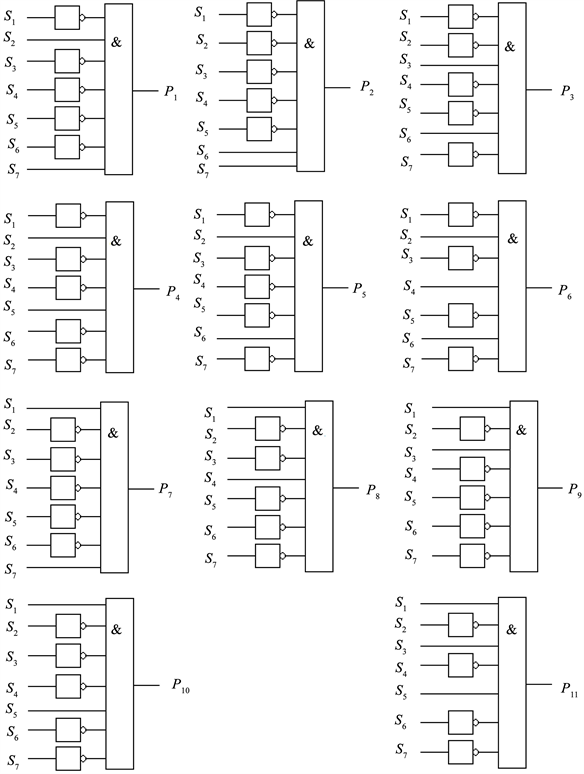

Figure 3. Circuit representation of R1
图3. R1的电路表示图
同样的,如果分别设 ,我们也可以得到 的电路图。如果将各个 的电路表示做成一个小的电路元件,那么以上的所有电路可以整合成如下的总电路图,如图4。
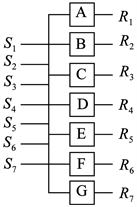
Figure 4. The digital circuit of FHP-II rule
图4. FHP-II规则的数字电路
其中,带小方格的 分别为表示 的电路元件。这样,只要输入一组 的值,我们便可以立即得到FHP-II规则下对应的 的值。
为了验证电路图的可靠性,我们给出所有的 的取值,利用上述电路图得出的 的值,与利用碰撞规则和Boolean动力学的结果完全一致。
3. 算例
作为算例,我们利用上面的逻辑电路生成Look-Up表进行计算。在程序中,先将Look-Up表读入内存,然后,在每个迭代步中进行查表。具体的例子是方腔流动。
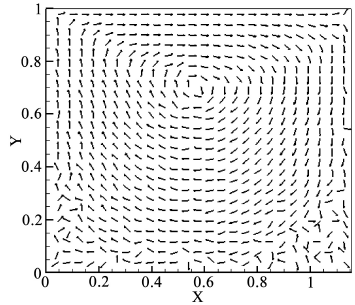
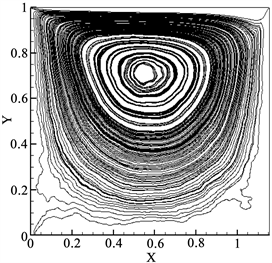
选择网格数128 × 128,方腔上边界速度U = 0.2,雷诺数Re = 30.71,迭代50,000步,从48,000步开始做时间统计平均。方腔的下、左、右边界均为无滑移边界条件 [12] ,在方腔上边界处放置一个均匀向右运动的薄板,这意味着上边界是均匀流动并且方腔内的流体质点运动到上边界后“回弹”至方腔流体内部。
从图5(a)中可以看到,方腔内部存在一个顺时针的大涡旋,方腔右下角处存在类似涡旋的混乱,图5(b)给出了方腔流动的流线图。可以清楚看到涡旋出现,再现了该问题经典算法的定性结果 [13]。
 (a)
(a)
 (b)
(b)
Figure 5. (a) Velocity field in square cavity flow, (b) Streamline
图5. (a) 方腔流动速度场,(b) 流线
4. 结论
本文给出了FHP-II格子气自动机的演化规则的数字逻辑电路,利用此逻辑电路达到的结果与利用碰撞规则和Boolean动力学的结果完全一致。在此基础上,我们计算了小雷诺数的方腔流动,结果是令人满意的。
Look-Up表的逻辑线路是格子气自动机电路的主要部分,仍然有许多问题需要研究,例如将流的过程加入数字电路中,更进一步,整体格子气自动机的线路的实现将是非常有意义的。
致谢
国家自然科学基金(NO. 11602033, NO. 11272133)资助。
文章引用
李 婷,王博宇,陈建华,闫广武. 用于流体力学的FHP-II格子气自动机的碰撞规则数字电路实现
Collision Rules and Digital Circuit Implementation of the FHP-II Lattice Gas Automata in Fluid Mechanics[J]. 流体动力学, 2018, 06(04): 143-149. https://doi.org/10.12677/IJFD.2018.64018
参考文献
- 1. Frisch, U., Hasslacher, B. and Pomeau, Y. (1986) Lattice Gas Automaton for the Navier-Stokes Equation. Physical Review Letters, 56, 1505-1508. https://doi.org/10.1103/PhysRevLett.56.1505
- 2. Wolfram, S. (1986) Cellular Automaton Fluids 1: Basic Theory. Journal of Statistical Physics, 45, 471-526. https://doi.org/10.1007/BF01021083
- 3. Frisch, U., d’Humières, D., Hasslacher, B., Lallemand, P., Pomeau, Y. and Riet, J.-P. (1987) Lattice Gas Hydrodynamics in Two and Three Dimensions. Complex Systems, 1, 649-707.
- 4. Clavin, P., d’Humieres, D., Lallemand, P. and Pomeau, Y. (1986) Cellular Automata for Hydrodynamics with Free Boundaries in Two and Three Dimensions. C. R. Acad. Sci. Paris II, 303, 1169-1174. https://www.researchgate.net/publication/279591285_Cellular_automata_for_hydrodynamics_with_ free_boundaries_in_two_and_three_dimensionsAutomates_cellulaires_pour_les_problemes_a_ frontieres_libres_en_hydrodynamique_a_deux_et_trois_dimensions
- 5. Vahala, L., Vahala, G. and Yepez, J. (2003) Lattice Boltzmann and Quantum Lattice Gas Representations of One-Dimensional Magneto Hydrodynamic Turbulence. Physics Letters A, 306, 227-234. https://doi.org/10.1016/S0375-9601(02)01599-2
- 6. Chen, H. and Metthaeua, W.H. (1987) New Cellular Automaton Model for Magneto Hydrodynamics. Physical Review Letters, 58, 1845-1848. https://doi.org/10.1103/PhysRevLett.58.1845
- 7. Montgomery, D. and Doolen, G. (1987) Two Cellular Automata for Plasma Computations. Complex Systems, 4, 831-838.
- 8. Clavin, P., Lallemand, P., Pomeau, Y. and Searby, G.Y. (1988) Simulation of Free Boundaries in Flow Systems by Lattice-Gas Models. Journal of Fluid Mechanics, 188, 437-464. https://doi.org/10.1017/S0022112088000795
- 9. 陈建华. FHP-II格子气自动机的碰撞规则及数字电路实现[D]: [硕士学位论文]. 长春: 吉林大学, 2018.
- 10. 王博宇. 用于求解流体动力学问题的FHP-II格子气自动机及程序实现[D]: [硕士学位论文]. 长春: 吉林大学, 2017.
- 11. Wolf-Glodrow, D.A. (1991) Lattice-Gas Cellular Automata and Lattice Boltzmann Models. Sprin-ger-Verlag Berlin Heidelberg.
- 12. 闫广武. 二维直角弯道中粘性流动的格子气体仿真[D]: [硕士学位论文]. 长春: 吉林大学, 1988.
- 13. Yan, B. and Yan, GW. (2011) A Steady-State Lattice Boltzmann Model for Incompressible Flows. Computers and Ma-thematics with Applications, 61, 1348-1354. https://doi.org/10.1016/j.camwa.2010.12.078
NOTES
*通讯作者。
