Geomatics Science and Technology
Vol.
07
No.
02
(
2019
), Article ID:
29912
,
7
pages
10.12677/GST.2019.72017
Mathematical Transformation of Latitude and Longitude Network on Several World Map Projections
Yexun Zhong1,2,3,4, Jiaqi Liu1, Baoqing Hu2,3
1Department of Navigation Engineering, Naval University of Engineering, Wuhan Hubei
2Key Laboratory of Beibu Gulf Environment Change and Resources Use, Ministry of Education, Guangxi Teachers Education University, Nanning Guangxi 3Guangxi Key Laboratory of Earth Surface Processes and Intelligent Simulation (Guangxi Teachers Education University), Nanning Guangxi
4Guangxi Regional Geographical Information Bureau of Surveying and Mapping, Nanning Guangxi
Received: Apr. 4th, 2019; accepted: Apr. 19th, 2019; published: Apr. 26th, 2019

ABSTRACT
The normal cylindrical projection, pseudo-cylindrical projection, and polyconic projection have different configuration of the longitude and latitude network, but they all belong to the contract graphics. And they all have the characteristics of symmetry transformation with the central meridian λ0 as the axis of symmetry when in the east-west direction, as the equator s0 as the axis of symmetry when in the north-south direction. Also, they all belong to a central symmetrical figure centered on the intersection O of the central meridian and the equator. According to the configuration features and spatial structure of the non-central meridians λi, a convex curved longitude net and a discrete straight longitude net are defined in this paper. According to the configuration characteristics and spatial structure of the non-zero latitudes φj, the inner convex coaxial circular arc latitude net and the equatorial parallel latitude net are defined. On this basis, the mathematical definitions of normal cylindrical projection, pseudo cylindrical projection and polyconic projection are given by the combination of different latitude and longitude nets. According to the rules of set operations, the mathematical transformation between different types of map projections is explained in this paper.
Keywords:Map Projection, Central Meridian, Web of Meridian and Parallel, Reflex Transformation
几种世界地图投影的经纬网的数学变换
钟业勋1,2,3,4,刘佳奇1,胡宝清2,3
1海军工程大学导航工程系,湖北 武汉
2南宁师范大学,北部湾环境演变与资源利用省部共建教育部重点实验室,广西 南宁
3南宁师范大学,广西地表过程与智能模拟重点实验室,广西 南宁
4广西测绘地理信息局,广西 南宁
收稿日期:2019年4月4日;录用日期:2019年4月19日;发布日期:2019年4月26日

摘 要
正圆柱投影、伪圆柱投影和多圆锥投影的经纬网的构形不同,但它们都属于合同图形,都具有以中央经线λ0为对称轴的东、西向镜射变换和以赤道s0为对称轴的南、北向镜射变换的特点。都属于以中央经线和赤道交点O为中心的中心对称图形。根据非中央经线λi构形特点和空间结构,定义了外凸型曲经线网、离散型直经线网;根据非零纬线φj的构形特点和空间结构,定义了内凸同轴圆弧型纬线网、赤道平行线型纬线网。在此基础上,通过不同经纬网的组合,给出了正圆柱投影、伪圆柱投影和多圆锥投影的数学定义。根据集合运算的规则,阐释了不同类型地图投影间的数学变换。
关键词 :地图投影,中央经线,经纬网,镜射变换

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
正圆柱投影、伪圆柱投影和多圆锥投影,常用作世界地图的数学基础 [1] [2] [3] 。这几种世界地图都具有中央直经线,其赤道也表象为直线的特点。因其同时具有以中央直经线 为对称轴的东、西轴对称和以赤道 为对称轴的南、北对称,所以它们又是以中央经线和赤道交点O为中心的中心对称的图形,也就是说正圆柱投影、伪圆柱投影和多圆锥投影,都属于合同图形 [4] [5] [6] 。这三种地图投影,它们在共性的基础上,又以各自的经纬网构形特点和变形分布的差异而展现着彼此间的典型特性。在变形性质上,正圆柱投影因经纬线相互正交使其具有等角投影、等积投影和任意投影各种变形性质,著名的墨卡托(Mercator)投影就属于等角圆柱投影 [7] 。伪圆柱投影由于其纬线全部表象为直线,而非中央经线又是对称于中央经线的曲线,所以除在赤道上能使经纬线正交外,其他地方的经纬线都斜交,这就意味着伪圆柱投影不可能有等角投影,它只有等积投影和任意投影。桑逊投影(Sanson)投影(或称Sanson-Flaamsteed投影)就是正弦曲线等面积伪圆柱投影;爱凯特(Eckert)投影则是极点投影成直线的等面积伪圆柱投影;摩尔威德(Mollweide)投影是椭圆经线等面积伪圆柱投影 [8] 。用于世界地图的多圆锥投影,为了使角度变形和面积都较适中,往往在变形性质上都属于任意投影,例如,等差分纬线多圆锥投影(中国地图出版社1963年方案)、吻接圆弧边经线多圆锥投影等 [9] [10] 。数学的抽象性帮助我们抓住事物的共性和本质,数学赋予知识以逻辑的严密性和结论的可靠性,正如爱因斯坦所说:“数学给精密自然科学以某种程度的可靠性,没有数学,这些科学是达不到这种可靠性的 [11] ”。正圆柱投影、伪圆柱投影和多圆锥投影,虽然经纬网构形的外观差异很大,但从经纬线方程的数学本质和内在联系分析,它们之间又有着密切的联系。常规地图投影变换中,从不动点子集包含着经线族还是纬线族及其结构特点,对应着确定的地图投影 [12] ;对常规地图投影在合同图形的共性中寻求其差异和特点,揭示其数学本质,正是为了使地图投影的基于不同标志的分类具有某种程度的可靠性。本文是笔者关于这几种地图投影的经纬线的数学表述和变换的研究和探讨。
2. 合同图形
定义 1 合同图形 图形 和 的点一一对应,并且 和 上的每两点间的距离等于 上的两对应点的距离,则称 和 为合同图形。合同图形的集合记为H。
定义 2 镜射变换 对平面上的定直线l,使得原象点M与象点 之间的线段 被l垂直平分的变换,叫做以l为轴的射影变换,简称镜射(也称反射) [13] ,以l为轴的镜射常记为 。
在数学中习惯以横轴为X轴,纵轴为Y构建平面直角坐标系。而在测绘学中则相反,以X为纵轴,Y为横轴。在常规地图投影中,又有多种以中央直经线 为对称轴的镜射变换。因此,测绘学中以中央直经线 为对称轴的镜射变换为:
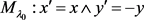 (1)
(1)
在用于世界地图的正圆柱投影、伪圆柱投影和多圆锥投影中,还存在以赤道 为对称轴的镜射变换。以 为对称轴的南北向的镜射变换为:
(2)
定义 3 中心对称 若两图形点一一对应,对应点连线被某一定点平分,则称此两图形为中心对称,该定点称为对称中心。
在用于世界地图的正圆柱投影、伪圆柱投影和多圆锥投影中,中央直经线 和赤道 的交点O,1象限和3象限,2象限和4象限的对应点,总被O等分,所以整个图形构成中心对称。具有轴对称或中心对称的图形必为合同图形。
3. 用于世界地图的正圆柱投影、伪圆柱投影和多圆锥投影的经纬网
设地图为D,
为其经纬网,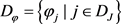 为纬线网,
为经线网,
为经纬网。为了区分不同的地图投影,分别用
表示正圆柱投影、伪圆柱投影和多圆锥投影的经纬网。由于这三类地图投影同时具备以中央经线
为对称轴的东、西对称,又具有以赤道
为对称轴的南、北对称,从而都具有以中央经线
和赤道
交点O为中心的中心对称。根据这三种世界地图投影的共同点得:
为纬线网,
为经线网,
为经纬网。为了区分不同的地图投影,分别用
表示正圆柱投影、伪圆柱投影和多圆锥投影的经纬网。由于这三类地图投影同时具备以中央经线
为对称轴的东、西对称,又具有以赤道
为对称轴的南、北对称,从而都具有以中央经线
和赤道
交点O为中心的中心对称。根据这三种世界地图投影的共同点得:
(3)
在 的条件下,地图的经纬网具有以中央经线 为轴的东西对称:
(4)
具有以中央经线 为轴的东、西对称的经纬网,属于镜射变换。 和 互为镜射变换 [14] 。
根据 的构形特点和空间结构,可定义不同类型的经线网络。
3.1. 外凸型曲经线族
平面曲线的自然方程是
,曲线的基本定理表明,曲线由其自然方程唯一决定。其中
为曲率,s为弧长。曲率(curvature)是曲线上邻近两点切向量夹角对弧长的变化率,它反映了曲线的弯曲程度 [15] 。伪圆柱投影和多圆锥投影的经线,可以是圆、椭圆、正弦曲线或多圆弧吻接曲线等,不管是什么类型的曲线,都是东、西对称的外凸曲线,离中央经线愈远曲率愈大。凸曲线的曲率大于零,直线的曲率为零,所以,中央直经线也就是曲率为零的曲线。由于赤道以南部分的经线可以通过以赤道
为对称轴的镜射变换获得,中央直经线西边部分又可通过以
为对称轴的镜射变换获得,故曲经线的数学描述只要对第一象限部分进行数学描述即得。设
为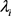 上
点处的曲率。
点处
点处的
的经切线的斜率。在此基础上,可定义外凸型曲经线:
上
点处的曲率。
点处
点处的
的经切线的斜率。在此基础上,可定义外凸型曲经线:
定义 4 外凸型曲经线 ,满足下列条件的点集:
(5)
称为外凸型曲经线。 经 的东、西和 的南、北镜射变换即得全图的外凸型曲经线集 ,地图的经线网还包括中央经线 ,所以外凸型曲经线网 ,记作 。
3.2. 离散型直经线族
定义 5 离散型直经线 ,满足下列条件的点集:
(6)
称为离散型直经线。 经 的东、西和 的南、北镜射变换即得全图的离散型直经线集 ,地图的经线网还包括中央经线 ,所以离散型直经线网 ,记作 。
3.3. 内凸同轴圆弧型纬线族
定义 6 内凸同轴圆弧型纬线族 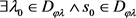 ,设
,满足下列条件的点集:
,设
,满足下列条件的点集:
(7)
则称集合 为内凸同轴圆弧型纬线族, 经以赤道 为对称轴的南、北镜射变换后得全图的内凸同轴圆弧型纬线集 ,地图的纬线网还包括赤道 ,所以纬线网 ,记作 ,称为内凸同轴圆弧型纬线网。
(7)式表明,非零纬线为同轴( )圆弧,圆心为 ,半径为 ,它们是凸部指向赤道的曲线族。
3.4. 赤道平行线型纬线族
定义 7 赤道平行线型纬线族 ,满足下列条件的点集:
(8)
(8)式表明,非零纬线均为半径为无穷大的圆弧,也就是直线。于是,
,这是赤道平行线型纬线网,又可表达为
,记作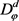 。
。
4. 正圆柱投影、伪圆柱投影和多圆锥投影的构成和投影变换
在给出外凸型曲经线网、离散型直经线网、内凸同轴圆弧型纬线网和赤道平行线型纬线网的基础上,通过不同经线网和纬线网的组合,可得正圆柱投影、伪圆柱投影和多圆锥投影的经纬网 [16] 。
4.1. 正圆柱投影
定义 8 正柱投影 离散型直经线网 和赤道平行线型纬线网 ,这两种经纬网的并集:
(9)
称为圆柱投影。图1。

Figure 1. Cylindrical projection
图1. 正圆柱投影图
4.2. 伪圆柱投影
定义 9 伪柱投影 外凸型曲经线网 和赤道平行线型纬线网 ,这两种经纬网的并集:
(10)
称为伪圆柱投影。图2。
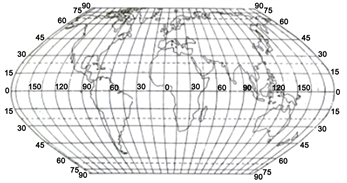
Figure 2. Pseudo-cylindrical projection
图2. 伪圆柱投影图
4.3. 多圆锥投影
定义 10 多圆锥投影 外凸型曲经线网 和内凸同轴圆弧型纬线网 ,这两种经纬网的并集:
(11)
称为多圆锥投影。图3。
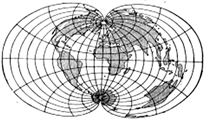
Figure 3. Polyconic projection
图3. 多圆锥投影
4.4. 多圆锥投影–伪圆柱投影变换
多圆锥投影 与内凸同轴圆弧型纬线网 的集差再与赤道平行线型纬线网 的并集,即为伪圆柱投影:
(12)
4.5. 伪圆柱投影–圆柱投影变换
伪圆柱投影 与外凸型曲经线网 的集差再与离散型直经线网 的并集即为圆柱投影:
(13)
4.6. 伪圆柱投影–多圆锥投影变换
伪圆柱投影 与赤道平行线型纬线网
的集差再与内凸同轴圆弧型纬线网
的并集即为多圆锥投影:
与赤道平行线型纬线网
的集差再与内凸同轴圆弧型纬线网
的并集即为多圆锥投影:
(14)
也可用伪圆柱投影 与空集的交集再与多圆锥投影的并集生成:
(15)
总之,在已给出的多种经纬网基本类型的基础上,按照集合运算的差集、交集、并集等集合运算的规则,一定能实现从初始经纬网到目标经纬网的变换 [17] 。
5. 结论
正圆柱投影、伪圆柱投影和多圆锥投影的经纬网的构形外观上有明显的差别,但它们都具有以中央经线 为对称轴的东、西向镜射变换和以赤道 为对称轴的南、北向镜射变换的特点,也即具有以中央经线 和赤道 交点O为中心的中心对称,都是满足合同图形定义的图形结构。根据非中央经线λj的构形特点和空间结构,给出了外凸型曲经线网、离散型直经线网的定义;根据非零纬线φj的构形特点和空间结构,给出了内凸同轴圆弧型纬线网、赤道平行线型纬线网的定义。在此基础上,通过不同经纬网的组合,构建了正圆柱投影、伪圆柱投影和多圆锥投影。又根据集合运算的差集、并集等规则,阐释了不同类型地图投影间的数学变换。
基金项目
国家自然科学基金项目(41671459;41661021;41571441);广西自然基金创新团队项目(2016JJF15001)。
文章引用
钟业勋,刘佳奇,胡宝清. 几种世界地图投影的经纬网的数学变换
Mathematical Transformation of Latitude and Longitude Network on Several World Map Projections[J]. 测绘科学技术, 2019, 07(02): 117-123. https://doi.org/10.12677/GST.2019.72017
参考文献
- 1. 胡毓钜, 龚剑文. 地图投影[M]. 第二版. 北京: 测绘出版社, 1992.
- 2. 胡毓钜, 龚剑文. 地图投影图集[M]. 第三版. 北京: 测绘出版社, 2006.
- 3. 钟业勋, 胡宝清. 数理地图学[M]. 第二版. 北京: 测绘出版社, 2017.
- 4. 钟业勋, 童新华, 李占元. 若干常规地图投影的数学定义[J]. 桂林理工大学学报, 2011, 31(3): 391-394.
- 5. 吴迪, 钟业勋, 胡宝清, 等. 系列世界地图的经纬网数学模型研究[J]. 海洋测绘, 2018, 38(2): 61-65.
- 6. 钟业勋, 胡宝清, 童新华, 等. 地图学概念的数学表述研究[M]. 北京: 科学出版社, 2015.
- 7. 方炳炎. 地图投影计算用表[M]. 北京: 测绘出版社, 1979.
- 8. 祝国瑞. 地图学[M]. 武汉: 武汉大学出版社, 2004.
- 9. 吴忠性, 胡毓钜. 地图投影论文集[M]. 北京: 测绘出版社, 1983.
- 10. 吴忠性, 杨启和. 数学制图学原理[M]. 北京: 测绘出版社, 1989.
- 11. 张燕顺. 数学的美与理 [M]. 第二版. 北京: 北京大学出版社, 2012.
- 12. 钟业勋, 边少锋, 胡宝清, 等. 基于不动点子集的常规地图投影分类体系[J]. 广西师范学院学报, 2018, 35(3): 56-60.
- 13. 汪罗淼, 严虹, 廖义琴. 几何学概论[M]. 北京: 清华大学出版社, 2011.
- 14. 刘佳奇, 钟业勋, 胡宝清, 等. 基于镜射变换的地图投影新定义体系[J]. 黑龙江工程学院学报, 2017, 31(3): 1-4.
- 15. 谷超豪. 数学词典[M]. 上海: 上海辞书出版社, 1992.
- 16. 钟业勋, 胡毓钜, 童新华. 基于不同经纬线类型组合的地图投影新定义[J]. 海洋测绘, 2012, 32(6): 13-16.
- 17. 楼世博, 孙章, 陈化成. 模糊数学[M]. 北京: 科学出版社, 1985.