Creative Education Studies
Vol.
07
No.
04
(
2019
), Article ID:
31619
,
6
pages
10.12677/CES.2019.74076
A Study of Classroom Teaching of New Mathematic Lessons
—Teaching and Inspiration of “Maximum (Minimum) Value and Derivative of Function”
Jiaying Zhu
Santai Middle School, Mianyang Sichuan

Received: Jul. 18th, 2019; accepted: Aug. 1st, 2019; published: Aug. 8th, 2019

ABSTRACT
This paper describes the teaching process of the first class hour of “Maximum (Minimum) Value and Derivative of Function” in detail. During this process, under the guidance of heuristic teaching principles, students are naturally introduced to enter the learning of new knowledge by means of question-and-answer, which motivates their interest in learning and enables them to actively participate in the lesson. Some pieces of inspiration can be obtained from the teaching of this lesson: the importance of natural guidance in teaching new mathematic lessons; the significance of students-oriented classroom teaching mode; the mathematics teaching concept that practice is much better than just viewing; the necessity of knowledge summary. Finally, this paper analyzes and summarizes the shortcomings and expectations of this lesson.
Keywords:Maximum and Minimum Values of Function, Derivative, Inspiration, Teaching Process
数学新授课课堂教学研究
——“函数的最大(小)值与导数”的教学与感悟
朱珈莹
三台中学,四川 绵阳

收稿日期:2019年7月18日;录用日期:2019年8月1日;发布日期:2019年8月8日

摘 要
本文详细记述了“函数的最大(小)值与导数”第一课时的教学过程,以启发式的教学原则为指导,通过问答的方式自然引导学生进入新知识的学习,激发学生的学习兴趣,使学生积极主动参与到课堂中来。从本节课的教学中得到几点启发:数学新授课中自然导入的重要性;学生为主体的课堂教学模式至关重要;百看不如一练的数学教学观;知识总结的必要性。最后分析总结了本节课的不足及期望。
关键词 :函数最值,导数,感悟,教学过程

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 基本情况
1.1. 授课对象
学生来自高二理科平行班,基础一般,思维较敏捷,解题能力参差不齐。
1.2. 教材分析
“函数的最大(小)值与导数”是《普通高中课程标准试验教科书·数学(选修2-2)》第一章“导数及其应用”中的内容。在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高、效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题,而导数是求函数最大(小)值的有力工具。本节课是在学生已经学习了单调性与导数、极值与导数的基础之上,进一步研究最值与导数的关系,符合学生的认知发展规律,使学生的知识层层递增,环环相扣,进而深化了对数学本质的理解和知识的同化。
教学目标:1) 借助函数图象,直观地理解函数的最大值和最小值的概念;2) 弄清函数最大值、最小值与极大值、极小值的区别与联系,理解和熟悉函数f(x)必有最大值和最小值的充分条件;3) 掌握求在闭区间[a,b]上连续函数f(x)的最大值和最小值的思想方法和步骤。
教学重、难点:利用导数研究函数最大值、最小值的问题。
教学方法:发现式、启发式。
教学基本环节:复习回顾→情境导入、展示目标→合作探究、精讲点拨→当堂检测、反思总结。
2. 教学过程
2.1. 复习函数单调性与导数、极值与导数
问题1:我们前面学习了单调性与导数,极值与导数,下面同学们回想一下函数极值的定义是什么?(投影显示极值定义的表格)
生:异口同声的回答出来。
问题2:求极值的步骤有哪些?
生:回答后投影显示出来极值的步骤。
极值的步骤:1) 求 ;2) 令 ,求根;3) 列表;4) 求极值。
练习:求函数 的极值。
解: ,令 ,解得 x = ±2 ,
当 ,则 或 ;
当 ,则 ,
所以 的极大值为 ,极小值为 。
师:同学们能不能画出这个函数的大致图象呢?
于是学生开始画图象,半分钟后,纷纷展示自己的成果,最后老师投影展示图象,和同学们画的基本一致。
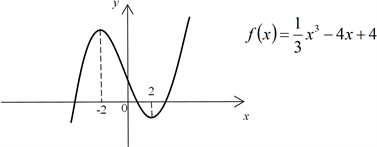
师:这个函数有没有最大值和最小值呢?
生:没有最大值也没有最小值。
师:为什么呢?
生:因为函数图象向两边无限延展。
师:那什么是函数的最大值和最小值呢?(学生说完,老师投影并说明)
2.2. 新课的引入
最大值:一般地,设函数 的定义域为I,如果存在实数M满足:1) 对于任意的 ,都有 ;2) 存在 ,使得 。那么称M是函数 的最大值 [1] 。
最小值:一般地,设函数 的定义域为I,如果存在实数m满足:1) 对于任意的 ,都有 ;2) 存在 ,使得 。那么称m是函数 的最小值。
下面同学们小组讨论函数 分别在区间[−3,5],[−3,3],[−3,0],[−1,1],(−3,0)上是
否有最大值和最小值,如果有,分别在哪点处取到?并把下面的表格填完整(五分钟小组讨论,小组中有的同学计算,有的同学说明,有的同学记录;还有的小组分工,每人求一个区间上的最值。时间到,老师叫一名同学代表来说明,同时老师在投影上显示函数在区间上的图象,并填写表格)


师:通过以上讨论分析,同学们能得出什么结论?
一名学生:函数在闭区间内必有最大值和最小值,在开区间不一定有最大值和最小值。
师:非常好,其他同学还有没有补充呢?
一名同学:从图像中看,函数图象是连续不断的。
师:特别棒,那么把两位同学说的总结起来,就得到了函数最值存在的充分条件了。(投影显示(1))
1) 函数的最大(小)值的存在性:一般地,函数y = f(x)在闭区间[a,b]上的图象是一条连续不断的曲线,那么它必有最大值和最小值 [2] 。
师:如何求函数在闭区间[a,b]上的最值呢?(可以从图中观察)
一名学生:比较函数极值与端点值的大小。
师:非常好,但是老师强调一点,这里的函数极值指的是所给区间内的极值。(投影显示)
2) 求最值的方法:比较(所给区间内的)函数极值与端点值的大小,其中最大的是最大值,最小是的最小值。
师:为什么要强调函数图象在闭区间是一条连续不断的曲线呢?同学们请看大屏幕
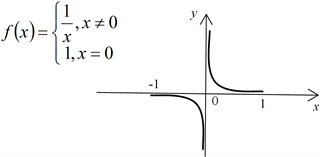
师:对于这个分段函数在闭区间[−1,1]上有没有最大值和最小值呢?
生:没有。
师:所以说如果函数图象在闭区间内不是连续曲线,则它不一定有最值。
师:对于函数在非闭区间上的最值问题我们要最好是数形结合,从图像中找是否有最值的问题。
例1:求函数 在闭区间[−3,0]上的最大值和最小值 [3] 。
解: ,令 ,则 ,在[−3,0]上, 时, ; 时, 在[−3,−1]上递增,[−1,0]上递减,极大值为 ,又 , 的最大值为3,最小值为−17。
练习1:教材31页练习题(2),(3),(4),(三名同学黑板演示,其他同学分小组做题。)
练习2:函数 的值域是_________。
练习3:函数 的最大值为_________。
例2:已知函数 , 的最大值为3,最小值为−29,求a,b的值。
解: ,
令 ,得 , (舍去)。
, ,
,
,
,
① 当 时,与题设矛盾。
② 当 时,f(x)的最大值为 ,f(x)的最小值为 , ;
③ 当 时,f(x)的最小值为 ,f(x)的最大值为 , 。
综上可得, , 或 , 。
2.3. 课堂小结
1) 求函数 在[a,b]上的最大值与最小值的步骤
① 求函数 在(a,b)内的极值;
② 将函数 的各极值与 端点 处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是 最小值。
2) ① 求闭区间上的最大值时,可只比较极大值和端点值;
② 求最小值时,可只比较极小值和端点值;
③ 如果函数在所给区间是单调函数,在端点处取得最值。
④ 如果区间中只有一个极值,那么这个极值通常就是函数的一种最值 [4] 。
2.4. 课后思考
已知 在 与 处都取得极值,若对 ,不等式 恒成立,求c的取值范围。
变式:若对 ,不等式 恒成立,c的取值范围又是什么?
2.5. 作业
教材32页6题。
3. 教学感悟
3.1. 数学新授课中自然导入的重要性
如果每堂新课开始都直接讲解今天要学习的新内容,没有过渡和连接,那么这堂课就会显得很不自然,难融入。而为了引起学生注意,迅速集中思维,老师往往在讲授新课前有一个与新知识相关的导入,激发学生的学习兴趣,产生学习动机,使学生自然进入最佳学习状态。并且导入的自然性所产生的情境和状态能使学生加深对知识的记忆,同时给以后的知识再认和知识再现提供一个良好的回忆场景,所以导入必须要自然,语言要流畅,让学生欣然接受新概念,积极探索新知识。
3.2. 学生为主体的课堂教学模式至关重要
传统的教学模式是以“教师教,学生学”为主要活动方式的课堂教学,限制了学生的思维和创造性。根据新课程改革的具体目标,改变课程过于注重知识传授的倾向,强调形成积极主动的学习态度,使获得基础知识与基本技能的过程的同时成为学会学习和形成正确价值观的过程。所以现在的教学不仅注重教学结果,更注重学生的学习过程,从关注学科转向关注学生,这样才有利于学生的全面发展。同时,以学生为主体的课堂教学模式更有利于培养学生自主学习的能力,独立思考和解决问题的能力,创新思维的能力,使学生成为有独立意识的主体,充分发挥学生的潜能。
3.3. 百看不如一练的数学教学观
数学是一门重理论、严谨性强、思维强、运算强的一门基础学科,所以要求学生不仅要记忆理解概念,同时思维要灵活。要想掌握知识点并能灵活应用就必须在理解知识的基础上让学生亲自动手演练加以巩固,这样才能加深记忆,避免遗忘,所以课堂上要做到讲练结合,把课堂交给学生,让学生动起来,整个课堂才能达到满意的效果。如果学生只是一味地看老师在黑板上的演示而不动手操作,那么下次再出现这样的类型题时学生只是感觉见过,讲过,但仍然不会解题。出现这样问题的原因就是没有亲自实践,导致思维不够连贯,知识掌握不到位,所以说百看不如一练。
3.4. 知识总结的必要性
一节课的内容讲完,学生练习完过后,还有一个重要的环节不能遗漏,那就是“课堂小结”。可以先让学生自己总结,然后找一名代表发言,其余同学补充,最后老师再进行总结。总结内容应侧重于方法的归纳和规律的总结,对易错点、易混淆点进行强调,补充学生没有总结到的内容,对整节课的知识进行梳理,最后形成知识网络。只有这样学生才能够系统地掌握知识。如果一节新授课没有知识总结,那么学生对这节课的知识点和题型是很模糊的,而如果对整节课的知识进行梳理,形成知识网络之后,学生就会又快又准地记住本节课的内容,并且知识框架也有利于学生在复习时能准确地回忆、重拾学习过的内容,因此知识总结是很有必要的 [5] 。
4. 本节课的不足与期望
由于一节课40分钟有限,所以给学生充分时间练习求函数在闭区间上的最值问题之后,求参数问题就显得有些匆忙;其次在讲解题时,应注意数形结合,让学生有数学形结合的思想,这样能快速准确地将题解答出来,本节课虽然也有数形结合,但是没有让学生形成数形结合来解题的想法,所以这一点需要加强。
总之,我们要改变传统的教学模式和学习方式,不断地探索和发掘学生的潜能,注重以学生为主体,教师为指导的教学方式,同时也鼓励学生在课堂上多采用研究性学习,合作性学习和自主学习的方式;而老师应严格把握好课堂的每一环节,不要出现时间上前松后散或前散后松的情况,要环环相扣,使学生理解和掌握当堂所学知识,这样我们的教学才是令人满意的教学。
文章引用
朱珈莹. 数学新授课课堂教学研究——“函数的最大(小)值与导数”的教学与感悟
A Study of Classroom Teaching of New Mathematic Lessons—Teaching and Inspiration of “Maximum (Minimum) Value and Derivative of Function”[J]. 创新教育研究, 2019, 07(04): 445-450. https://doi.org/10.12677/CES.2019.74076
参考文献
- 1. 中学数学课程教材研究开发中心. 普通高中课程标准试验教科书数学必修1A版[M]. 北京: 人民教育出版社, 2007.
- 2. 中学数学课程教材研究开发中心. 普通高中课程标准试验教科书数学选修2-2A版[M]. 北京: 人民教育出版社, 2007.
- 3. 颜世芹. 浅谈导数在求函数最值中的应用[J]. 数学学习与研究, 2012(3): 87.
- 4. 周学勤. 导数求最值与最优化[J]. 吕梁教育学院学报, 2008, 25(4): 56-57+70.
- 5. 付禹. 高中生学习导数及其应用时的困难点研究[D]: [硕士学位论文]. 长春: 东北师范大学, 2015.