Pure Mathematics
Vol.07 No.04(2017), Article ID:21347,6
pages
10.12677/PM.2017.74037
A kind of Analysis of the Multi-Prime Goldbach’s Issues
Yunhua Cui
Unit95899, beijing

Received: Jun. 23rd, 2017; accepted: Jul. 6th, 2017; published: Jul. 13th, 2017

ABSTRACT
The applications of prime distribution theory with the new train of thought are researched upon prime groups with restraint. The minimum amounts of the multi-prime Goldbach's issues are deduced by expanding the analysis and conclusions in odd Goldbach’s prime groups.
Keywords:Prime Distribution, Goldbach's Conjecture, Odd Goldbach's Conjecture, Multi-Prime Goldbach’s Issue
多素数哥德巴赫问题的一种分析
崔蕴华
95899部队,北京
收稿日期:2017年6月23日;录用日期:2017年7月6日;发布日期:2017年7月13日

摘 要
研究素数分布理论新思路对约束素数组的实际应用,将奇数哥德巴赫猜想的分析方法和结论推广到多素数哥德巴赫问题,并得出了最小数量的结论。
关键词 :素数分布,哥德巴赫猜想,奇数哥德巴赫猜想,多素数哥德巴赫问题

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
递推采用素数消元法,可方便地将3素数哥德巴赫命题 [1] 结论推广到4素数与任意多素数。
2. 命题1:(多素数哥德巴赫命题)
满足 的
的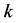 素数哥德巴赫数组数量表示为
素数哥德巴赫数组数量表示为
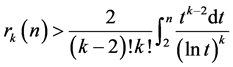 (1)
(1)
并展开为渐近级数
 (2)
(2)
式中 为
为 对渐近级数式的最佳截断
对渐近级数式的最佳截断
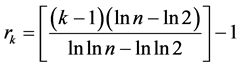 (3)
(3)
 以首项表为
以首项表为
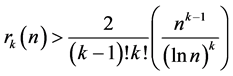 (4)
(4)
证明:
1) 3素数推广到4素数
令素数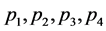 满足
满足
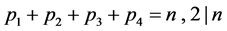 (5)
(5)
设式(5)中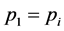 遍取不超过
遍取不超过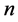 的全部素数
的全部素数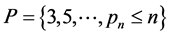 ,
,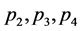 将满足约束条件
将满足约束条件

即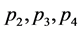 为
为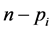 的3素数数组。
的3素数数组。
与3素数命题 [1] 同理,由此构造的 必穷尽全部组合,且数组数量大于实际组合数的4倍。当正整数
必穷尽全部组合,且数组数量大于实际组合数的4倍。当正整数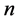 比较大
比较大 时,引用3素数命题数量下限2阶简化式(4.14) [1] ,并将
时,引用3素数命题数量下限2阶简化式(4.14) [1] ,并将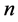 改写为
改写为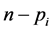
 (6)
(6)
对集合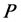 构造集合
构造集合
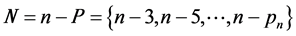
显然,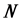 内各元素对应的3素数数组求和并取1/4,为4素数题解。即
内各元素对应的3素数数组求和并取1/4,为4素数题解。即

将式(6)代入得
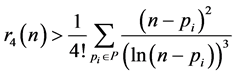 (7)
(7)
同3素数命题分析,对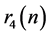 在
在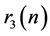 基础上作进一步的数量下限估计,并引用
基础上作进一步的数量下限估计,并引用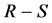 积分结论
积分结论
 (8)
(8)
以最低门限方式表为
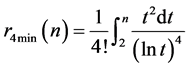 (9)
(9)
以式
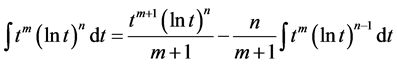
对式(9)分部积分得
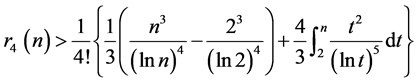
以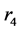 表渐近级数的最佳截断,进一步展开为渐近级数
表渐近级数的最佳截断,进一步展开为渐近级数
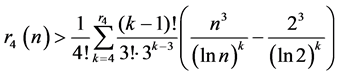
即
 (10)
(10)
只取首项并忽略积分下限项为
 (11)
(11)
以最低门限方式表为
 (12)
(12)
与奇数哥德巴赫命题同法可确定最佳截断为
 (13)
(13)
当 充分大时,式(13)可近似为
充分大时,式(13)可近似为
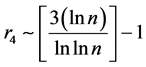 (14)
(14)
2) 4素数推广到任意 素数
素数
采用递推方法,在满足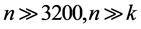 的条件下,可将多素数组数量下限的结论由4素数递推到5素数,6素数,
的条件下,可将多素数组数量下限的结论由4素数递推到5素数,6素数,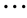 ,
,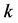 素数命题。计算出由3素数到
素数命题。计算出由3素数到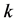 素数数量下限的对数积分式、首项表达式有关参数,列入表1。
素数数量下限的对数积分式、首项表达式有关参数,列入表1。
由表1,当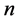 比较大
比较大 时,
时,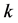 素数命题数量的对数积分表为
素数命题数量的对数积分表为
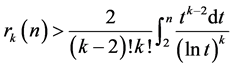 (15)
(15)
以最低门限方式表为
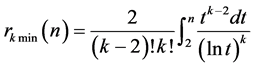 (16)
(16)
以 表
表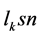 的最佳截断,可将对数积分式(16)展开为渐近级数
的最佳截断,可将对数积分式(16)展开为渐近级数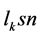

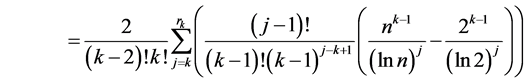
 (17)
(17)
与奇数哥德巴赫命题同法可证明相应最佳截断为

取
 (18)
(18)
当 很大时
很大时
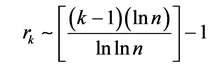 (19)
(19)
式(1)(2)成立。
对式(17)仅取首项为
 (20)
(20)
以最低门限方式表为
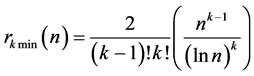 (21)
(21)
命题1证毕。
3. 实例2:(多素数哥德巴赫数组例)
对 (偶)或
(偶)或 (奇),对应
(奇),对应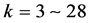 按式(21)计算出相应
按式(21)计算出相应 列入表2,表中同时列出自由度
列入表2,表中同时列出自由度 ,渐近级数式首项阶数
,渐近级数式首项阶数 ,相应由式(18)表示的最佳截断
,相应由式(18)表示的最佳截断 和渐近级数的有效项数
和渐近级数的有效项数 。
。
为避免表格过大,表中数据的选择不满足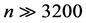 ,对说明表中各项参数关系是有效的。
,对说明表中各项参数关系是有效的。
Table 1. The related parameters about the quantity limit of multi-prime propositions to logarithmic integral type and first expression
表1. 多素数命题数量下限对数积分式、首项表达式有关参数
Table 2. The relational table between and
表2.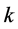 与
与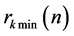 对关系表
对关系表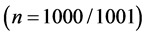
1) 增大时,以
增大时,以 对应的多素数组数求和代替
对应的多素数组数求和代替 对应的多素数组数求和造成的误差增大;
对应的多素数组数求和造成的误差增大; 增大时,每次递推以首阶代替各阶求和引进的误差增大,递推次数增多引起误差积累加大。因此
增大时,每次递推以首阶代替各阶求和引进的误差增大,递推次数增多引起误差积累加大。因此 较大时,数量下限
较大时,数量下限 将越发远离实际数量
将越发远离实际数量 ,但这并不影响数量下限的理论意义,它从数量的角度证明了多素数哥德巴赫数组的存在性,并给出任何情况下总能满足的下限数量。
,但这并不影响数量下限的理论意义,它从数量的角度证明了多素数哥德巴赫数组的存在性,并给出任何情况下总能满足的下限数量。
2) 当 由
由 逐步递增时,由于自由度加大,
逐步递增时,由于自由度加大,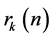 首先单调递增,直到对
首先单调递增,直到对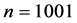 对应
对应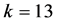 出现最大值
出现最大值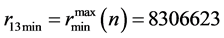 ,对
,对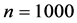 对应
对应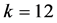 出现最大值
出现最大值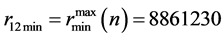 ;
;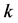 再增大时,由于自由度过大,可选择的组合数单调递减,直到对
再增大时,由于自由度过大,可选择的组合数单调递减,直到对 对应
对应 出现最小值
出现最小值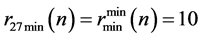 ;对
;对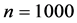 对应
对应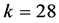 出现最小值
出现最小值 。
。
致谢
青年高级工程师王炜华博士、汤宏伟、王远和李军博士完成了文献 [1] 的仿真计算,崔雁巍完成了文档整理和校对,在此表示衷心感谢。感谢爱妻邢纪荣和家人的理解、支持和关爱。
文章引用
崔蕴华. 多素数哥德巴赫问题的一种分析
A kind of Analysis of the Multi-Prime Goldbach’s Issues[J]. 理论数学, 2017, 07(04): 282-287. http://dx.doi.org/10.12677/PM.2017.74037
参考文献 (References)
- 1. 崔蕴华, 素数分布研究新思路的若干应用, 前沿科学, 2016, 10(4): 26-45.
