Pure Mathematics
Vol.08 No.01(2018), Article ID:23645,24
pages
10.12677/PM.2018.81011
Study of Singular Internal Boundary Problems for m Dimensional Anisotropic Heat Conduction Equations
Xiaoqing Wu
College of Science, Southwest Petroleum University, Chengdu Sichuan

Received: Jan. 3rd, 2018; accepted: Jan. 20th, 2018; published: Jan. 31st, 2018

ABSTRACT
In this paper, first of all, the mathematical model I is established on anisotropic heat conduction equation in m dimension infinite domain. Mathematical model I: seek
, make it satisfy to
(I)
The free term of the equation is
, among them,
is m dimensional Diracfunction,
is strength function of singular source. The exact solution
of the mathematical model I is obtained by the matrix theory and the generalized eigenfunction method, under the condition that the matrix
is real symmetric positive definite matrix and
. The matrix B is a lower triangular matrix, whose main diagonal element is positive. The singular internal boundary is demonstrated as
. We establish the free boundary problem IIa and problem IIb on homogeneous heat conduction equation. The problem IIa is free boundary problem in region
. The problem IIb is free boundary problem in region
. It is also solves these two questions of problem IIa and IIb. These two free boundaries are the same
.
Keywords:Heat Conduction Equation, Multidimensional (m Dimensional), Anisotropy, Free Boundary Problem, Real Symmetric Positive Definite Matrix

m维各向异性热传导方程的奇异内边界问题研究
吴小庆
西南石油大学理学院,四川 成都

收稿日期:2018年1月3日;录用日期:2018年1月20日;发布日期:2018年1月31日

摘 要
本文首先建立m维无穷区域
中各向异性的热传导方程的数学模型I;寻求向量函数
使所求问题的解函数
在任意时刻
在该向量函数上取区域
中的正的最大值,即
称向量函数
为最佳热源边界。并把该问题称为奇异内边界问题。数学模型I(m维无穷区域各向异性非齐次热传导方程齐次初始条件的奇异内边界问题):求
,使其满足
(I)
其中:
为m维狄拉克d-函数;热传导方程的系数矩阵
为m阶实对称非负矩阵。本文应用矩阵理论和广义特征函数法,在条件A为m阶实对称正定矩阵,
(
为正线下三角矩阵)下,获得了数学模型I的充分光滑的精确解
,其中奇异内边界的表达式是
。同时获得了m维各向异性齐次热传导方程的自由边界问题IIa和问题IIb的充分光滑的精确解,且两者的自由边界都是相同的m维向量函数表达式
。
关键词 :热传导方程,多维(m维),各向异性,自由边界问题,实对称正定矩阵

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
一个偏微分方程的定解问题,若其定解区域的部分边界是待定的,它和定解问题的解彼此相关且必
须同时确定。这类定解问题,人们称之为自由边界问题,其待定边界称为自由边界。所有自由边界问题都是非线性问题。自由边界问题的研究有着广泛的实际背景。在渗流力学、等离子物理、塑性力学、射流等方面都提出了各种不同形式的定常和不定常自由边界问题 [1] - [12] 。为了研究m维各向异性热传导方程的自由边界问题,我们建立起相应的m维各向异性热传导方程的奇异内边界问题。本文假设在区域
存在无重点的一条奇异内边界
;向量函数
把
分成
和
两部分,
,满足条件
,
;
把区域
分成两个区域
和
,
,
(空集);在
和
两个区域都分别满足齐次的m维各向异性热传导方程,在奇异内边界
上热传导方程具有一定奇性,在整个区域
用具有特殊自由项
的非齐次m维各向异性热传导方程来描述奇异内边界上的奇性,
为m维狄拉克d-函数,
为奇异源强度函数。其中奇异内边界
是待定的,它和问题的解函数
彼此相关且必须同时确定。
显然寻求
与寻求
是等价的。我们同时求
,使其满足数学模型I。称数学模型I为奇异内边界问题。即有
数学模型I (m维无穷区域各向异性非齐次热传导方程齐次初始条件的奇异内边界问题):
求
,使其满足
(I)
应用矩阵理论和广义特征函数法,在条件
为m阶实对称正定矩阵,
(
为正线下三角矩阵)下,获得了数学模型I的充分光滑的精确解
。同时获得了m维各向异性齐次热传导方程的自由边界问题IIa和问题IIb的充分光滑的精确解。问题IIa和问题IIb具有公共的自由边界
。称m维向量函数表达式
为最佳热源边界。表达式
满足条件
;其中
,
。公式表明m维向量
由m维热传导方程中出现的所有参数
唯一确定。
2. 符号说明
m为某正整数;
为m阶实矩阵,
表示
的转置矩阵;
实数集
;
m维列向量的集合
;
向量函数:
;
;
;
;
;
;
;
;
m维开区间:
;
m维闭区间:
;
多元(m元)函数
;
的连续映射,是定义域是
,值域在
中的函数。函数的支集
,支集的闭包
;
记函数集合
。
3. 主要结果
3.1. m维无穷区域各向异性非齐次热传导方程非齐次初始条件的初值问题的求解
定解问题I (m维无穷区域各向异性非齐次热传导方程非齐次初始条件的初值问题):
定理3.1.1 (定解问题I的精确解):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵);
2)
,
为充分光滑的单调函数,
;
3)
;
4)
;
则定解问题I有充分光滑的精确解
(4)
其中
(5)
(6)
定解问题I的求解过程:
记偏微分算子
(7)
先考虑m维线性常系数偏微分方程在无界区域
的特征值问题I
(8)
为求解特征值问题I和定解问题I我们建立了引理3.1.1~引理3.1.6。
引理3.1.1:设
为m阶实对称正定矩阵,则存在正线下三角矩阵
满足
且分解是唯一的;且有
1) 正线下三角矩阵
的行列式
;
2) 记
,则
为正线上三角矩阵,
;
3) 记
,
;则当
,有
;当
,有
。
3)' 当
,有
;当
,有
。
证明:由矩阵理论的结论 [13] 即知存在正线下三角矩阵
满足
且分解是唯一的。由
有
。
正线下三角矩阵
,正线下三角矩阵
的行列式
,且
;
的转置矩阵
为正线上三角矩阵。
的逆矩阵
为正线上三角矩阵。
。
下证3) 由于
为正线上三角矩阵,即有
和
;从而有
为列向量,应用分块矩阵的乘法运算即有
(9)
从而有
(10)
由于
即有
(11)
为正定矩阵,则
为正定矩阵,
为正定二次齐式,从而有
(12)
(13)
由
的任意性,分别令
,
其中
。
由(13)式即有
即
(14)
再记
;有
和
(15)
由(14),(15)两式即有:当
,
,有
;显然也有:
当
,
,有
。由(10)式:
(16)
结论也可表述为:3)' 当
,有
;当
,有
。引理证毕。
记
,作
到
的线性变换
(17)
记
(18)
引理3.1.2:若
,则有
(19)
其中
(20)
为向量偏微分算子。
证明:由(17)式即有
(21)
由(18)式即有
(22)
由复合函数的求导法则,即有
(23)
即(19)式成立。引理证毕。
m维二阶线性偏微方程在无界区域
的特征值问题II
(24)
其中
(25)
(26)
引理3.1.3:若
,则特征值问题I中方程(8)与特征值问题II中方程(24)等价。
证明:由
,有
(27)
记
,由引理3.1.1矩阵
为正线上三角矩阵。
由(18)式有
(28)
由矩阵乘法
(29)
从而
(30)
(31)
由于
为正线上三角矩阵,有
(32)
记
(33)
即有
(34)
由(27),(34)两式即知方程(8)与方程(24)等价。引理证毕。
引理3.1.4:特征值问题II的特征值
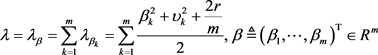 (35)
(35)
所对应的特征函数为
(36)
其中
,
。
证明:由分离变量法容易求解特征值问题II:
令
(37)
则
(38)
(39)
(40)
(41)
(42)
(43)
(44)
(45)
由(45)式,(25)式即有(35)式成立。由(37)式,(43)式即有(36)式成立。引理证毕。
由(17)和(18)式换回原变量即得特征值问题I的特征函数。于是得到
引理3.1.5:特征值问题I的特征值
(46)
所对应的特征函数为
(47)
其中
,
。
证明:
(48)
(49)
引理证毕。
引理3.1.6:特征值问题I的特征函数系
是无界区域
带权函数
的完备正交系;正交关系即
(50)
证明:由于
(51)
变量替换
(52)
则
(53)
(54)
即有变量替换的雅可比行列式
(55)
由多重积分变量替换公式,即有
(56)
引理证毕。
由引理3.1.5与引理3.1.6的结论可以引入广义特征函数法 [11] [12] 求解定解问题I。
不妨设解
,将其表为特征函数的积分形式
(57)
将上式两边乘以
再关于变量
在
积分,利用正交关系(50)则有
 (58)
(58)
得到
(59)
将方程中的自由项
也表为特征函数的积分形式
(60)
由(59)即有
(61)
应用d-函数的积分性质即
(62)
含参变量积分与算子
的运算交换次序即有
(63)
且有
(64)
由(2)式即有
(65)
(66)
将(60) (63) (64)式代入方程(1)即有
(67)
由特征函数系的完备正交性即有
(68)
从而得到非齐次常微分方程的初值问题
(69)
用常数变易法得到非齐次常微分方程的初值问题的解为
(70)
(71)
(72)
(73)
(74)
将(62)代入方程(74)即有
由于
即知
(75)
将(66)式代入(73)式即有
(76)
由于
即有
(78)
即定解问题I的解中
的表达式(78)式即知(5)式成立,解中
的表达式(75)式即(6)式成立。定理3.1.1证毕。
附注3.1.1:在定理3.1.1的条件4)下,易证(5)式右端积分在
绝对一致收敛,则所表示的
在
连
续,即
;且易证
。
3.2. m维无穷区域各向异性热传导方程的奇异内边界问题
数学模型I (m维无穷区域各向异性非齐次热传导方程齐次初始条件的奇异内边界问题):
求
,使其满足
定理3.2.1 (数学模型I的精确解):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵);
2)
,
为充分光滑的单调函数,
;
3)
;
则数学模型I的充分光滑的精确解为
:
证明:定解问题I的精确解
表达式(6)即有(83)式满足(79)式,(80)式,(82)式三式。再令
(85)
下面由引理3.2.1和引理3.2.2完成定理3.2.1的证明;也可以由引理3.2.3和引理3.2.4完成定理3.2.1的证明。记
(86)
引理3.2.1:(86)式等价于(84)式。
证明:由(86)即有恒等式
(87)
令
即得
在上式两端左乘
矩阵即有
(88)
即得(84)式。反之(84)式成立,
,有
和
两式,两式相减则有恒等式
;在上式两端左乘
矩阵即有(86)式成立。
引理3.2.2:若(83)式,(84)式成立;则有(81)式成立。
证明:若(84)式成立,则有(86)式成立,即有
(89)
由(83)式,故有(81)式成立。证毕。
由引理3.2.1和引理3.2.2即知(83) (84)式满足(81)式,从而满足数学模型I。证毕。
引理3.2.3:当(83)和(84)式成立时,则有
(a)
;(b)
。
证明:由于
(90)
(91)
(92)
(93)
由(93)即知,(84)式成立的充要条件是
(94)
又由
(95)
(96)
(97)
(a)
即有
(98)
由引理3.1.1中3)'的结论即得
;再由(95)式即有
(99)
从而有
(100)
同理
(b)
(101)
从而有
(102)
引理3.2.3证毕。
记
(103)
引理3.2.4:由(83)式确定的
,使得(84)式与(103)式等价。
证明:由(95)式即知,当且仅当(94)式成立有(103)式成立。从而当且仅当(84)式成立时有(103)式成立。
引理3.2.4证毕。
当(83)和(84)式成立时,有引理3.2.3,引理3.2.4成立,从而有(103)式,(100)式,(102)式成立,推出(81)式成立。由此也得到定理3.2.1的证明。证毕。
附注3.2.1:定理3.2.1中解
由(83)式给出,它依赖于奇异源强度函数
的确定。由(83)式,(86)式即知
(104)
若边值函数
为已知函数,则
(105)
是关于奇异源强度函数
作为未知函数的第一类Volterra积分方程。
附注3.2.2:奇异源强度函数
也可以是广义函数,此时积分方程为
(105)'
例如,若边值函数为
,容易验证
是满足积分方程(105)'的解。
定解问题II (m维无穷区域各向异性齐次热传导方程非齐次初始条件的初值问题):
由定理3.1.1即知定解问题II的解由(5)式给出。
定理3.2.2 (定解问题II的解的性质定理):若
由(84)式表出;则
2) 当
;定解问题II的充分光滑的精确解可表为
(109)
且
;
,满足
。
2) 当
;定解问题II的充分光滑的精确解可表为
(110)
且
,满足
;
3) 当
;定解问题II的充分光滑的精确解可表为
(111)
且
,满足
。
证明:1) 当
;且
则由(5)式,定解问题II的解可表为
(112)
(113)
(114)
(115)
满足
。
与下面2)中的证明方法类似可证:
;
。
2) 当
;定解问题II的充分光滑的精确解
可由(110)表出,记
由(110)有
(116)
(117)
(118)
(119)
(120)
由
有
即
(121)
再由引理3.1.1中3)'的结论即得
(122)
从而
(123)
即有
(124)
故满足
;
3)当
;定解问题II的充分光滑的精确解
可由(111)式表出。当
;
(125)
与2)中证明类似,由引理3.1.1中3)'的结论即得
(126)
从而
(127)
故满足
。证毕。
数学模型II (m维无穷区域各向异性非齐次热传导方程非齐次初始条件的奇异内边界问题):
求
使其满足
定理3.2.3 (数学模型II奇异内边界问题解的存在定理):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵),
2)
,
3)
;
则数学模型II存在充分光滑的精确解
:
其中
(134)
(135)
证明:由定理3.2.1,定理3.2.2即得。证毕。
推论3.2.1 (数学模型II奇异内边界问题解的存在定理):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵);
2)
;
3)
;
则数学模型II存在充分光滑的精确解
:
其中
(138)
(139)
3.3. m维各向异性齐次热传导方程非齐次初始条件的自由边界问题IIa和IIb
问题IIa (m维各向异性齐次热传导方程非齐次初始条件在区域
上的自由边界问题):
求
,使其满足
定理3.3.1 (自由边界问题IIa解的存在定理):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵),
2)
,
3)
;
则自由边界问题IIa存在充分光滑的精确解
:
其中
(146)
(147)
证明:由于当
时,
,故当
时,
满足齐次方程(140),从而(144)式满足(140) (141) (143)三式;由引理3.2.3证明中(100)式有
,又定理3.2.2证明了
满足
;即有
即得(142)式成立。证毕。
推论3.3.1 (自由边界问题IIa解的存在定理):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵),
2)
3)
;
则自由边界问题IIa存在充分光滑的精确解 :
:
其中
(150)
(151)
问题IIb (m维各向异性齐次热传导方程非齐次初始条件在区域
上的自由边界问题):
求
,使其满足
定理3.3.2 (自由边界问题IIb解的存在定理):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵);
2)
,
3)
;
则自由边界问题IIb存在充分光滑的精确解
:
其中
(158)
(159)
证明:由于当 时,
,故当
时,
满足齐次方程(152),从而(156)式
时,
,故当
时,
满足齐次方程(152),从而(156)式
满足(152) (153) (155)三式;由引理3.2.3证明中(102)式
,
定理3.2.2证明了
满足
即得
即得(154)式成立。证毕。
推论3.3.2:(自由边界问题IIb解的存在定理):若
1)
为m阶实对称正定矩阵,
(
为正线下三角矩阵);
2)
;
3)
;
则自由边界问题IIa存在充分光滑的精确解
:
其中
(162)
(163)
4. 结论
I) 对于在m维(m为某正整数)无穷区域
的抛物型方程的不定常自由边界问题,可以转化为相应的奇异内边界问题来研究。假设在区域
存在一条无重点的奇异内边界
建立奇异内边界问题数学模型I。所求得的向量函数
就是问题IIa和问题IIb的公共自由边界。
II) 在条件
为m阶实对称正定矩阵,
(
为正线下三角矩阵)下;获得了无穷区域
的m维各向异性热传导方程的自由边界问题IIa和问题IIb存在充分光滑的精确解。问题IIa和问题IIb具有公共的自由边界:
,其中
,
。公式表明m维向量
由m维各向异性的热传导方程中出现的所有参数
唯一确定。
文章引用
吴小庆. m维各向异性热传导方程的奇异内边界问题研究
Study of Singular Internal Boundary Problems for m Dimensional Anisotropic Heat Conduction Equations[J]. 理论数学, 2018, 08(01): 75-98. http://dx.doi.org/10.12677/PM.2018.81011
参考文献 (References)
- 1. 姜礼尚. 期权定价的数学模型和方法[M]. 第2版. 北京: 高等教育出版社, 2008.
- 2. 刘文超, 姚军, 王建忠. 低渗透多孔介质非达西渗流动边界界面追踪[J]. 计算物理, 2012, 29(6): 823-827.
- 3. 崔晓丽, 刘威, 孟丽娜. 有相变的变系数抛物型微分方程自由边界问题[J]. 黑龙江工程学院学报, 2012, 26(2): 74-77.
- 4. 崔霞. 二维抛物型积分微分方程动边界问题的有限元方法[J]. 高等学校计算数学学报, 1999(3): 228-235.
- 5. 吴小庆. 二维非线性抛物型方程移动边界问题的近似解与广义解[J]. 西南石油学院学报, 1994, 16(增刊).
- 6. 刘文超, 姚军, 陈掌星, 刘曰武, 孙海. 一维低渗透多孔介质非达西渗流动边界模型的精确解析与数值解研究[J]力学学报, 2015, 47(4).
- 7. 王丽平. 与永久美式ESOs有关的一个自由边界问题[J]. 工程数学学报, 2014(4): 511-520.
- 8. 张恭庆, 姜礼尚. 稳态水锥的自由边界问题[J]. 科学通报, 1978, 23(11): 647-650.
- 9. 白东华, 孙顺华. 流体通过孔隙介质的一个自由边界问题[J]. 四川大学学报(自然科学版), 1981(1): 6-15.
- 10. 黄少云, 王耀东. 稳态水锥自由边界问题及其数值逼近[J]. 北京大学学报(自然科学版), 1983(1): 3-25.
- 11. 吴小庆. 多资产期权确定最佳实施边界问题的研究[J]. 理论数学, 2016, 6(6): 496-526.
- 12. 吴小庆. 不定常自由边界问题研究[J]. 理论数学, 2017, 7(2): 104-135.
- 13. 史荣昌. 矩阵分析[M]. 北京: 北京理工大学出版社, 1996.








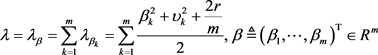 (35)
(35) (58)
(58) :
: 时,
,故当
时,
满足齐次方程(152),从而(156)式
时,
,故当
时,
满足齐次方程(152),从而(156)式