Pure Mathematics
Vol.
09
No.
05
(
2019
), Article ID:
31492
,
9
pages
10.12677/PM.2019.95084
Matched Pair and Manin Triple of Hom-Malcev Algebra
Jinyuan Li
Liaoning Normal University, Dalian Liaoning
Received: Jul. 2nd, 2019; accepted: Jul. 22nd, 2019; published: Jul. 29th, 2019

ABSTRACT
In this paper, we study matched pair and Manin triple of Hom-Malcev algebra. First, we give the definition of matched pair of Hom-Malcev algebra and the method of getting a new Hom-Malcev algebra on the direct sum of two Hom-Malcev algebras, we also study the method of constructing a new Hom-Malcev algebra on the dual space of Hom-Malcev algebra. Then, we give the definition of Manin triple of Hom-Malcev algebra, and we give the relation between matched pair and Manin triple of Hom-Malcev algebra.
Keywords:Hom-Malcev Algebra, Matched Pair, Manin Triple
Hom-Malcev代数的配对和Manin Triple
李进圆
辽宁师范大学,辽宁 大连
收稿日期:2019年7月2日;录用日期:2019年7月22日;发布日期:2019年7月29日

摘 要
本文主要研究了Hom-Malcev代数的配对和Manin triple。首先给出Hom-Malcev代数的配对的定义以及在两个Hom-Malcev代数的直和上构造Hom-Malcev代数的方法,研究在Hom-Malcev代数的对偶空间上构造Hom-Malcev代数的方法。然后给出Hom-Malcev代数的Manin triple的定义,并给出Hom-Malcev代数的配对和Manin triple之间的关系。
关键词 :Hom-Malcev代数,配对,Manin Triple

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
作为李代数的推广,Malcev代数不仅和李代数之间存在着密切的联系,和交错代数之间也有着密切的关系。就像李群在单位元的切空间是李代数一样,局部解析的Moufang群的切空间也是一个Malcev代数 [1] 。在 [2] 中,作者不仅给出了Malcev代数的定义,还发现每一个交错代数都是可容许的Malcev代数。Hom-Malcev代数的定义是由Yau在 [3] 中给出的,并证明了每一个Hom-交错代数也都是可容许的Hom-Malcev代数。此后,许多学者对Hom-Malcev代数进行了研究,例如,在 [4] 中,作者证明了Hom-Malcev代数上的几个恒等式。在 [5] 中,作者研究了Hom-李代数上的Hom-Yang-Baxter方程以及Hom-李双代数。在 [6] 中,作者给出了Malcev代数上的Yang-Baxter方程以及Malcev双代数。因此,可以考虑的一个问题是在Hom-Malcev代数上是否也会存在类似于Hom-Yang-Baxter方程的方程以及Hom-Malcev双代数。
2. Hom-Malcev代数的定义和表示
定义2.1 [3] :设M是域F上的线性空间,
为代数同态,如果M中有二元双线性运算
,对于
,有
(2.1)
(2.2)
则称
为域F上的Hom-Malcev代数。
定义2.2 [7] :设
为Hom-Malcev代数,V为线性空间,
为线性映射,
,如果对于
,有
(2.3)
(2.4)
则称
为
的表示。
定义2.3 [7] :设
为Hom-Malcev代数,
为
的伴随表示,如果对于
,有
(2.5)
(2.6)
则称这个Hom-Malcev代数为相容的Hom-Malcev代数。
3. Hom-Malcev代数的配对
定义3.1:设
和
为Hom-Malcev代数,若
和
分别为
和
的表示,对于
,
,有
(3.1)
(3.2)
(3.3)
(3.4)
(3.5)
(3.6)
则称
为这两个Hom-Malcev代数的配对。
定理3.2:设
,
为Hom-Malcev代数,
和
为线性映射,在
上定义二元反对称双线性运算
,对于
,有
并定义
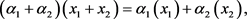
则
为Hom-Malcev代数当且仅当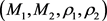 为
和
这两个Hom-Malcev代数的配对。
为
和
这两个Hom-Malcev代数的配对。
证明:
为Hom-Malcev代数当且仅当对于
,
,
(3.7)
(3.8)
成立。
(3.7)成立等价于(2.3)成立,(3.8)成立等价于这16种情况下(3.8)成立:
1)
,
;
2)
,
,
;
3)
,
,
;
4)
,
,
;
5)
,
,
;
6)
,
,
;
7)
,
, ;
;
8)
,
,
;
9)
,
,
;
10)
,
,
;
11)
,
,
;
12)
,
, ;
;
13)
,
, ;
;
14)
,
,
;
15)
,
, ;
;
16)
,
。
其中,情况1)下(3.8)成立
为Hom-Malcev代数,情况2) 3) 5) 9)下(3.8)成立
(2.4) (3.1)成立,情况8) 12) 14) 15)下(3.8)成立
(2.4) (3.2)成立,情况4) 7) 10) 13)下(3.8)成立
(3.3) (3.4)成立,情况6) 11)下(3.8)成立
(3.5) (3.6)成立,情况16)下(3.8)成立
为Hom-Malcev代数。
定理3.3:设
为Hom-Malcev代数,
为线性映射,在
上定义
(
),则
1)
为Hom-Malcev代数当且仅当
满足以下两个条件:
(3.9)
(3.10)
2)
为相容的Hom-Malcev代数当且仅当
满足(2.9)和(2.10)且
(3.11)
 (3.12)
(3.12)
证明:1)
为Hom-Malcev代数当且仅当对于
成立。因此,
,
等价于(3.9)成立。
等价于(3.10)成立。
2)
为相容的Hom-Malcev代数当且仅当1)且对于
。
,
成立。因此,
,
等价于(3.11)成立。
等价于(3.12)成立。
定理3.4:设
为相容的Hom-Malcev代数,线性映射
满足(3.9)~(3.12),在
上定义二元反对称双线性运算
,对于
,
,有
并定义
则 是Hom-Malcev代数当且仅当对于
,
,
满足
是Hom-Malcev代数当且仅当对于
,
,
满足
(3.13)
 (3.14)
(3.14)
(3.15)
(3.16)
(3.17)
(3.18)
证明:由定理3.2可知,
是Hom-Malcev代数当且仅当
为
和
这两个Hom-Malcev代数的配对,当且仅当
,
满足(3.1)~(3.6)即可。
定义3.5:设
为相容的Hom-Malcev代数,
为线性映射,若
满足(3.9)~(3.18),则称
为Hom-Malcev双代数。
4. Hom-Malcev代数的Manin triple
定义4.1:设
是Hom-Malcev代数,若
和
都为M的子代数,
,M上存在一个非退化的、对称的双线性函数
保持不变性,即
,有
(4.1)
 (4.2)
(4.2)
且
和
关于
都是迷向的,即
,则称
为Hom-Malcev代数
的Manin triple。
定理4.2:设
,
为相容的Hom-Malcev代数,
为
上的双线性函数,
,在
上定义运算
并定义

其中,
,
,则
是Hom-Malcev代数的配对的充分必要条件为
是Hom-Malcev代数的Manin triple。
证明:必要性。根据定理3.2可知,若
是配对,则
是Hom-Malcev代数。显然,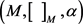 和
都为
的子代数。
和
都为
的子代数。
,取
,若
,则当
时,
可以得到
。同理,当
时,可以得到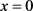 ,因此
,
是非退化的。
,因此
,
是非退化的。
可知
是对称的。
由
,可知(4.1)成立。
由
,可知(4.2)成立。因此,
是不变的。
由
,可知M关于
都是迷向的。同理,
关于
也是迷向的。综上所述,
是Manin triple。
充分性。若
是Manin triple,由定义4.1可知,
是Hom-Malcev代数,因此,由定理3.2可知,
是配对。
定理4.3:设
,
为相容的Hom-Malcev代数,则下列三个条件是等价的。
1)
为Hom-Malcev双代数。
2)
是Hom-Malcev代数的配对。
3)
是Hom-Malcev代数的Manin triple。
证明:由定理4.2和定义3.5可推出。
文章引用
李进圆. Hom-Malcev代数的配对和Manin Triple
Matched Pair and Manin Triple of Hom-Malcev Algebra[J]. 理论数学, 2019, 09(05): 632-640. https://doi.org/10.12677/PM.2019.95084
参考文献
- 1. Kerdman, F.S. (1979) Analytic Moufang Loops in the Large. Algebra and Logic, 18, 325-347.
https://doi.org/10.1007/BF01673501
- 2. Malcev, A.I. (1955) Analytic Loops. Matematicheskii Sbornik, 36, 569-576.
- 3. Yau, D. (2012) Hom-Maltsev, Hom-Alternative, and Hom-Jordan Algebras. International Electronic Journal of Algebra, 11, 177-217.
- 4. Issa, A.N. (2015) On Identities in Hom-Malcev Algebras. International Elec-tronic Journal of Algebra, 17, 1-10.
https://doi.org/10.24330/ieja.266209
- 5. Sheng, Y. and Bai, C. (2014) A New Approach to Hom-Lie Bialgebras. Journal in Algebra, 399, 232-250.
https://doi.org/10.1016/j.jalgebra.2013.08.046
- 6. Goncharov, M.E. (2012) Structures of Malcev Bialgebras on a Simple Non-Lie Malcev Algebra. Communications in Algebra, 40, 3071-3094.
https://doi.org/10.1080/00927872.2011.560587
- 7. 李进圆, 李艳朋. Hom-Malcev代数的表示[J]. 高师理科学刊, 2019, 39(3): 6-9.





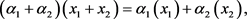
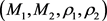 为
和
这两个Hom-Malcev代数的配对。
为
和
这两个Hom-Malcev代数的配对。 ;
; ;
; ;
; ;
; (3.12)
(3.12) 是Hom-Malcev代数当且仅当对于
,
,
满足
是Hom-Malcev代数当且仅当对于
,
,
满足 (3.14)
(3.14) (4.2)
(4.2)
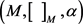 和
都为
的子代数。
和
都为
的子代数。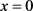 ,因此
,
是非退化的。
,因此
,
是非退化的。